基礎からのベイズ統計学 Skype読書会(13)：参加メモ

この勉強会に参加させていただきました： https://github.com/7shi/study/wiki/bayes_hmc
読んでいる本（出典）：基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門 | 豊田秀樹 | 本 | Amazon.co.jp
前回：基礎からのベイズ統計学 Skype読書会(10)：参加メモ - クッキーの日記

読んだ範囲： 115～125ページ
11、12回を欠席してしまったので流れがよくわかっていないけど後から読み返してメモ。

リープフロッグ法（109ページ）
- ハミルトンの運動方程式を数値的に解くときに、中点差分をつかうやり方をこういうらしい。
  - Leapfrog integration - Wikipedia, the free encyclopedia

ハミルトニアンモンテカルロ法（112ページ）

事後分布にしたがう乱数がほしい。
事後分布と、それとは独立な標準正規分布との同時分布にしたがう乱数でも別に構わない。

事後分布と標準正規分布の同時分布を書き下すと以下のようになる（章末問題の 8 問目を見据えて、尤度が試行回数 $n$ の二項分布、事前分布が母数 $\alpha,\,\beta$ のベータ分布の場合にしてみる）。
　 $\displaystyle f(\theta, p|x)=\exp \biggl[\log \bigl( f(\theta|x) \bigr) +\log \bigl( f(p) \bigr) \biggr]$
　　　　　　 $\displaystyle \propto \exp\biggl[\log \bigl( \theta^x (1-\theta)^{n-x} \theta^{\alpha-1} (1-\theta)^{\beta-1} \bigr)+\log \bigl( \exp(-\frac{1}{2}p^2) \bigr) \biggr]$
　　　　　　 $\displaystyle = \exp\biggl[ (\alpha + x -1) \log \theta + (\beta+n-x-1)\log (1-\theta)-\frac{1}{2}p^2 \biggr]$
　　　　　　 $\displaystyle = \exp\bigl[ -\mathcal{H}(\theta, p) \bigr]$
最後の解釈は、

位置-運動量空間	母数-標準正規分布にしたがう確率変数空間
位置 $\theta$	母数 $\theta$
運動量 $p$	標準正規分布にしたがう確率変数 $p$
ハミルトニアン	同時分布の対数の-1倍
ポテンシャルエネルギー	事後分布の対数の-1倍
位置エネルギー	標準正規分布の対数の-1倍

のときを図示してみると以下。
- 赤いところ：ハミルトニアンが大きくて、同時確率が低い。
- 青いところ：ハミルトニアンが小さくて、同時確率が高い。52ページによると事後確率最大値は $\hat{\theta}_{\rm MAP} = 0.657$ で、下の絵の青っぽいところもだいたいその辺にある気はする。
からリープフロッグ法で時間を何ステップか進めてみる（章末問題 8, 9）。
- $h(\theta) = - (\alpha + x -1) \log \theta - (\beta+n-x-1)\log (1-\theta)$ なので、 $h'(\theta) = - (\alpha + x -1) / \theta + (\beta+n-x-1) / (1-\theta)$ を111ページの式にあてはめればよい。
- 章末問題 9 で指示されている方の $\varepsilon=0.01$ をつかって、 $L=15$ ステップ動いた図が以下。上図では横のプロット範囲が狭かったので少し広げた。 $\varepsilon=0.05$ では軌跡がもっとカクカクしていた。
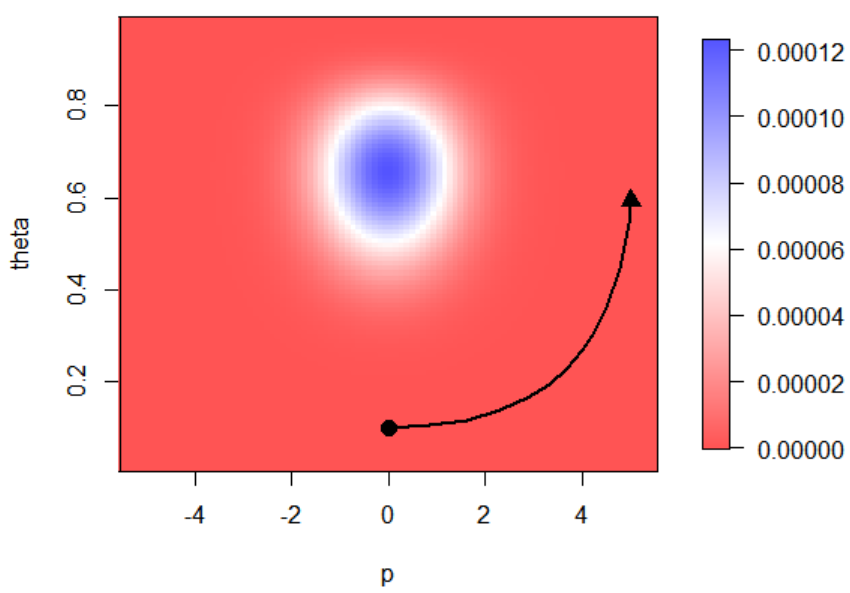
$L$ ステップ動いたらその点の受容／棄却を判断する（ほぼ受容されるはず）。新しい点 $(p_1, \, \theta_1)$ を受容したら、正規乱数 $\tilde{p}$ を発生させて $(\tilde{p}, \, \theta_1)$ にワープする。そこからまた $L$ ステップ動く。繰り返し。

$\theta$ のEAP推定値まで出してないけどお腹すいたので終わる。スクリプトは以下。

library(fields)

p <- seq(-5.5, 5.5, length.out=100)
theta <- seq(0.01, 0.99, length.out=100) # log(0) を避ける
H <- c()

for (i in 1:length(p)) {
  for (j in 1:length(theta)) {
    H <- c(H, 9.2 * log(theta[[j]]) + 4.8 * log(1 - theta[[j]]) - 0.5 * p[[i]] * p[[i]])
  }
}
H <- exp(H)

mycolors <- c(rgb(1,(84:256)/256,(84:256)/256), rgb((255:84)/256,(255:84)/256, 1)) # 赤～青グラデーション
image.plot(p, theta, matrix(H, ncol=100, byrow=TRUE), col=mycolors)
abline(v=c(-5.55), h=c(0.995)) # image.plot すると左辺と上辺の黒線が見えなくなるので描き足す苦肉の策

### リープフロッグ法

L <- 15
epsilon <- 0.01
p <- 0
theta <- 0.1
p.trace <- c(p)
theta.trace <- c(theta)

for (i in 2:L) {
  p <- p - 0.5 * epsilon * (-9.2/theta + 4.8/(1-theta))
  theta <- theta + epsilon * p
  p <- p - 0.5 * epsilon * (-9.2/theta + 4.8/(1-theta))
  p.trace <- c(p.trace, p)
  theta.trace <- c(theta.trace, theta)
}

#図示
points(p.trace[1], theta.trace[1], cex=1.5, pch=19)
lines(p.trace, theta.trace, lwd=2)
points(p.trace[L], theta.trace[L], cex=1.5, pch=17)