雑記 - クッキーの日記

お気付きの点がありましたらご指摘いただけますと幸いです。

まとめ
このブログ記事の証明はダイクストラ法を【解釈1】のように捉えているが、【解釈2】のように「Q からコスト最小のノードを取り出したときもうそのノードのコストはそれにしかならない」という方針で示す方が吞み込みやすいかもしれないしあまり変わらないかもしれない。

【解釈1】ダイクストラ法とは、安く行けるノードから収集していく方法である。
【解釈2】ダイクストラ法とは、到達コストが確定するノードから確定していく方法である。

Dijkstra's Algorithm：このブログ記事を書く前に Qiita に以下の記事を書いたときに実装を参考にした。

【Python】ダイクストラ法 + 可視化スクリプト #matplotlib - Qiita：こちらに書いた「もしノード0以外からノード3に行くならば、必ず他の暫定コストを経由しなければならない」が【解釈2】に近い。なお、この記事にリンクした可視化スクリプトはこれ以上ノードが増えるとみづらいし汎用性が低い。

数学的帰納法をわかりやすく【例題3問、応用5パターン】 | 高校数学の美しい物語：このブログ記事の補題アでパターン 3 の帰納法をつかっている。

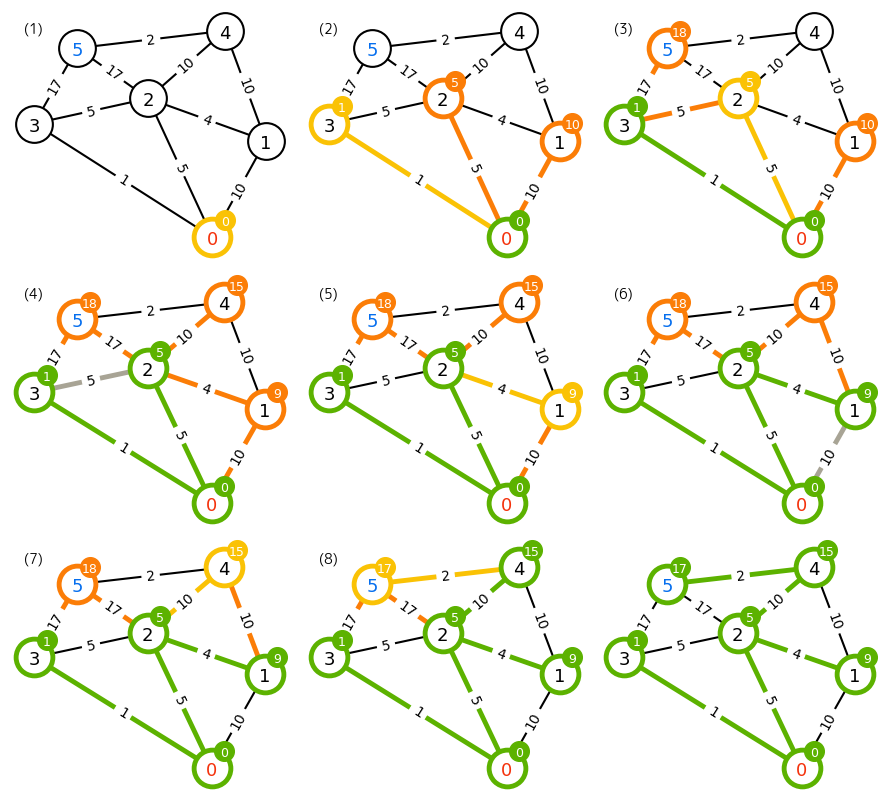
エッジの重みが非負の場合の単一始点最短経路問題を解くアルゴリズムにダイクストラ法なるものがあるのですね。なるほどアルゴリズムを実行してみると最短経路が出てくるようにみえますが、しかしなぜこのアルゴリズムで最短経路が出てくるといえるのでしょうか。

ノード0からの最小コストを求めていく経過
詳細：【Python】ダイクストラ法 + 可視化スクリプト #matplotlib - Qiita

ダイクストラ法の主張を書き下すと以下でしょうか。いまは計算量を議論したいのではないので、Q を優先度付きキューにするとよいなどは置いておきます。また、目標ノードまでの最小コストが達成される経路を取り出したいなら Q には〈コストいくらで, どのノードに行ける, どのノードのほうからきたとき〉というタプルを格納するべきですがそれも置いておきます。

N 個のノード 0, 1, ..., N-1 と、それらの間に張られるいくつかのエッジからなるグラフがあるとする。各エッジには非負のコストが付いているものとする (コストは向きによって違ってもよい)。
いま、ノード 0 からノード N-1 までの道が存在するものとするとき、ノード 0 からノード N-1 まで行く最小コストが以下のアルゴリズムで求まる。

空の集合 Q を用意する。＃〈コストいくらで, どのノードに行ける〉というタプルを格納する。
空の辞書 D を用意する。＃各ノードまでの最小コストがいくらに確定したかが格納される。
【手順0】Q に要素〈コスト=0, ノード=0 〉を追加する。
【手順1】Q からコスト最小の要素〈コスト=c, ノード=i 〉を取り出す。
【手順2】i が既に D のキーならば、【手順1】に戻る。
【手順3】i をキー、c を値として D に追加する。
【手順4】i=N-1 ならここで終了する。求める最小コストは c である。
【手順5】i からエッジがあるノード j のそれぞれに対して以下を実行し、【手順1】に戻る。
　 j が D のキーでないならば、Q に〈コスト=c+cost(i, j), ノード=j 〉を追加する。
　ただし cost(i, j) はノード i からノード j へエッジを通るときのコストである。

D には結果的に最小コストが確定したノードが溜まっていきます。対して Q は、D に確定ノードを追加するたびに「確定ノードから一歩でこのノードに行けるよ (それがそのノードまでの最小コストかはさておき)」といったいわば暫定ノードを溜める集合ですね。それで、とどのつまりダイクストラ法は Q からコスト最小の要素を取り出して D に追加していくというだけなのですが、明らかでないのはなぜこれで D に各ノードまでの確定最小コストが蓄積してくれるのかですね……。

まあしかし、現実として D に安く行けるノードから蓄積されていくことがわかっていますので、直接以下の補題が帰納法で示せるかやってみましょう。

補題ア．【手順3】を n 回目に通るときには、D に「n 番目に安く行けるノード及びそのコスト」が格納される。

補題アの証明．
帰納法で示す。まず、n=1 のとき、【手順3】を 1 回目に通るときには、D にノード 0 自身 (最も安く行けるノード) までのコスト 0 が格納されるので成り立つ。
次に、n=1, ..., k に対して、【手順3】を n 回目に通るときに、D に n 番目に安く行けるノード及びそのコストが格納されると仮定する。このとき、【手順3】を k+1 回目に通る直前の【手順1】の時点で、

Q に格納されているうちコスト最小のノードのコストが D に格納されている k 個のノードのうちの最大コストを下回ることはない (補題イ)。
D にも Q にも格納されていないノードであって Q 内の最安ノードより安く到達できるノードはない (∵ もしあるとすると、そのノードは D に格納されているノードから 2 歩以上先のはずだが、そこに至る 1 歩先のノードは必ず【手順5】で Q に格納されているはずなので、2 歩以上先により安く到達できることに矛盾する)。

が成り立つので、この【手順1】の時点の Q の最安ノードは k+1 番目に安く行けるノードとなり、【手順3】を k+1 回目に通るときには、D に「k+1 番目に安く行けるノード及びそのコスト」が格納される。
よって帰納法により、【手順3】を n 回目に通るときには、D に「n 番目に安く行けるノード及びそのコスト」が格納されることが示された。

補題イは別途証明しましょう。といってもアルゴリズム上明らかですが……。

補題イ．n 回目の【手順5】を終えた時点で、Q に格納されているうちコスト最小のノードのコスト q_n が D に格納されているうちの最大コスト d_n を下回ることはない (d_n ≦ q_n)。

補題イの証明．
帰納法で示す。n=1 のとき、1 回目の【手順3】で空の D に Q の唯一の要素であるノード 0 ( コスト 0 ) が移されて Q は空になり、その直後の 1 回目の【手順5】で Q にノード 0 からエッジがあるノードおよびそこまでのコストが格納されるが、任意のエッジのコストは非負なのでコスト最小エッジのコスト q_1 が d_1 = 0 を下回ることはない。
次に、n=k のとき、k 回目の【手順5】を終えた時点で、d_k ≦ q_k と仮定する。このとき、k+1 回目の【手順3】で D に Q から最小コスト q_k が移され、D の新しい最大コストが d_{k+1}=q_k となり、Q の新しい最小コストが q' ≧ q_k になり、その直後の【手順5】で Q にさっきのコスト最小のノードからエッジがあるノードおよびそこまでのコストが格納されるが、任意のエッジのコストは非負なのでコスト最小のエッジのコスト c' をとっても d_{k+1}=q_k≦min(q', q_k+c')=q_{k+1} である。
よって帰納法により、n 回目の【手順5】を終えた時点で、d_n ≦ q_n である。

証明できたと思いますが、この証明はダイクストラ法を【解釈1】のように捉えていますね。【解釈2】のように捉えて、Q からコスト最小のノードを取り出したときもうそのノードのコストはそれにしかならない、という方針で示す方が吞み込みやすいでしょうか……あまり変わらないでしょうか……。