クッキーの日記

DLM

状態空間モデル

位相的データ解析

R

数理論理学

本読みまとめ

勉強会参加ログ

このブログについて

github.com/CookieBox26/ML

Zenn

数式が崩れていたらその記事単体を表示すると解消するかもしれないです。

入門機械学習による異常検知―Rによる実践ガイド：ノート2

本読み機械学習

読んでいる本（出典）：入門機械学習による異常検知―Rによる実践ガイド | 井手剛 |本 | 通販 | Amazon

前回：ノート1 ／次回：ノート3
目次：入門機械学習による異常検知―Rによる実践ガイド

読んだページ： 23～44ページ
以下、メモと雑談。

前回までのあらすじ

観測値の異常度は、正常なデータ群の分布に対する対数尤度で測るよ。
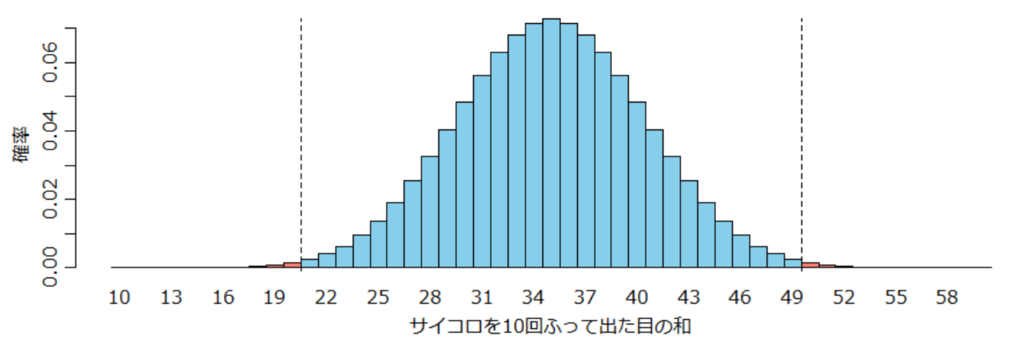
- 例．サイコロを10回ふって出た目の和が20以下か50以上になる確率は1%未満なので、もしサイコロをふった結果そうなってしまったらあまり尤もらしくなく、異常なのではないか（サイコロかあなたが）。
異常度の閾値をどう設定するべきかについて、観測データが i.i.d. に正規分布にしたがうなら、異常度が F 分布にしたがうよ（ホテリング理論）。
- 例．東京の2017年1月1日～18日の日ごとの平均気温は以下だった。気象庁｜過去の気象データ検索
  x <- c(7.4, 7.2, 8.0, 8.5, 6.7, 4.5, 4.1, 3.9, 7.2, 8.1, 6.9, 6.0, 6.2, 2.4, 0.7, 3.2, 5.4, 5.8)
  もし1月19日の平均気温が0℃だったら異常なのかどうか考える。日ごとの平均気温が i.i.d. に正規分布にしたがうと仮定するのは気象学的には駄目かもしれないけど、ここではいいことにして、「1% も起こりそうにないこと」を異常とみなすなら、0.30℃未満か 11.06℃超が異常になる。つまり、1月19日の平均気温が0℃なら異常である。
  > qnorm(mean=mean(x), sd=sqrt(var(x)*(18-1)/18), 0.005)
  [1] 0.2975372
  > qnorm(mean=mean(x), sd=sqrt(var(x)*(18-1)/18), 0.995)
  [1] 11.05802
  ただ、上の議論では、「1月1日～18日の平均気温は正規分布から歪んでいなかったのか」が考慮されていない。そもそも18点しかサンプルがないなら、平均や分散の推定値には区間幅があるだろう。それも考慮すれば、 $(x' - \hat{\mu})^2 / \hat{\sigma}^2 \sim (N+1)/(N-1) \cdot \mathcal{F}(1, N-1)$ が成り立つので（ホテリング理論）、以下のように正常と判定される範囲が少し広がり、-0.72℃未満か 12.08℃超が異常になる。つまり、1月19日の平均気温が0℃ならぎりぎり異常ではない。あまり0℃になってほしくはないけど。
  > F_0.01 <- qf(df1=1, df2=18-1, 0.99)
  > F_0.01
  [1] 8.39974
  > mean(x) - sqrt(var(x) * (18+1) / 18 * F_0.01)
  [1] -0.7220735
  > mean(x) + sqrt(var(x) * (18+1) / 18 * F_0.01)
  [1] 12.07763
  なお、各日の異常度とF分布上側1%の閾値ラインをプロットすると以下。1月1日～18日の平均気温に異常値はなかった。15日の日曜日は特に寒かったけど、異常ラインに達するほどではなかった。
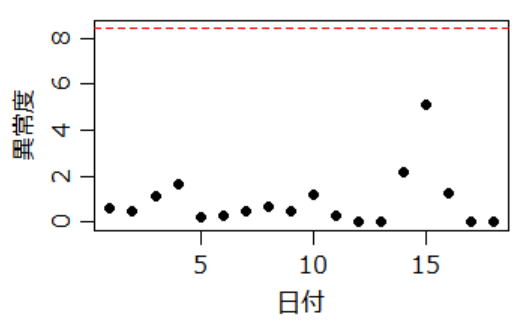
- 1変数のホテリング理論の証明（26～36ページ）について。
  - 定理2.3（30ページ）は以下でも示せる。
    正規分布の二乗和がカイ二乗分布に従うことの証明 | 高校数学の美しい物語
  - 式2.26（33ページ）の ${\rm H}_N$ について、 ${\rm H}_N = {\rm H}_N^{\rm T}$ かつ ${\rm H}_N^2 = {\rm H}_N$ に注意。
  - 定理2.5（35ページ）を、教科書のやり方を追っていないけど自分でやってみる。
    $x \sim \chi^2(m, a), \; y \sim \chi^2(n, b)$ のとき、 $\displaystyle z \equiv \frac{x/(am)}{y/(bn)} \sim \mathcal{F}(m, n)$ を示せ。
    とりあえず分布の式をちゃんと書いておく。
    $\displaystyle f_X(x) = \frac{1}{2a \Gamma (m/2)} \left( \frac{x}{2a} \right) ^{m/2 -1} \exp \left( -\frac{x}{2a} \right)$
    $\displaystyle f_Y(y) = \frac{1}{2b \Gamma (n/2)} \left( \frac{y}{2b} \right) ^{n/2 -1} \exp \left( -\frac{y}{2b} \right)$
    $\displaystyle f_Z(z) = \frac{\Gamma (m/2 + n/2)}{\Gamma(m/2) \Gamma(n/2)} \left( \frac{m}{n} \right) ^{m/2} z^{m/2 - 1} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2}$
    $w=y, \; z=bnx/(amy)$ に変数変換する。 $x = amwz/(bn), y = w$ のヤコビアンは、
    $\displaystyle J(w, z) = \begin{vmatrix} amz/(bn) & amw/(bn) \\ 1 & 0 \end{vmatrix} = -\frac{amw}{bn}$
    $w, \; z$ の同時確率密度関数は、統計検定の教科書の22ページより、
    $f_{WZ}(w, z) = f_{XY}\bigl( amwz/(bn), \; w \bigr) \bigl| J(w, z) \bigr|$
    　　　　　 $\; \displaystyle = \frac{1}{2a \Gamma (m/2)} \left( \frac{mwz}{2bn} \right) ^{m/2 -1} \exp \left( -\frac{mwz}{2bn} \right) \cdot \frac{1}{2b \Gamma (n/2)} \left( \frac{w}{2b} \right) ^{n/2 -1} \exp \left( -\frac{w}{2b} \right) \cdot \frac{amw}{bn}$
    　　　　　 $\; \displaystyle = \frac{z^{m/2 -1}}{2b \Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \left( \frac{w}{2b} \right) ^{(m+n)/2 - 1} \exp \left( -\frac{w}{2b} \bigl( \frac{mz}{n} + 1 \bigr) \right)$
    $z$ の分布を出すには、これを $w$ について積分して周辺化すればよい。
    $\displaystyle f_Z(z) = \int_0^{\infty} dw f_{WZ}(w, z)$
    　　　 $\displaystyle \, = \frac{z^{m/2 -1}}{2b \Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \int_0^{\infty} dw \left( \frac{w}{2b} \right) ^{(m+n)/2 - 1} \exp \left( -\frac{w}{2b} \bigl( \frac{mz}{n} + 1 \bigr) \right)$
    　　　 $\displaystyle \, = \frac{z^{m/2 -1}}{\Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2} \int_0^{\infty} dt \cdot t ^{(m+n)/2 - 1} \exp (-t)$
    　　　 $\displaystyle \, = \frac{\Gamma (m/2 + n/2)}{\Gamma(m/2) \Gamma(n/2)} \left( \frac{m}{n} \right) ^{m/2} z^{m/2 - 1} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2}$
    なんかちゃんと出たからこれでいいや。

今回のお話

データが多次元正規分布にしたがう場合も、同様にで異常度を定義できる。
- これもマハラノビス距離の2乗。雑記 - クッキーの日記
- 例．東京の2017年1月1日～18日の最低／最高気温は以下だった。気象庁｜過去の気象データ検索
  x1 <- c(2.0, 3.8, 3.5, 3.6, 3.7, 1.5, 0.1, 1.6, 3.8, 3.5, 3.9, 0.7, 1.4, -1.3, -2.3, -2.0, 0.7, 1.1)
  x2 <- c(13.8, 13.3, 13.7, 14.0, 10.4, 8.8, 8.7, 6.0, 11.1, 12.7, 11.0, 12.1, 12.7, 6.3, 4.7, 8.0, 10.9, 10.3)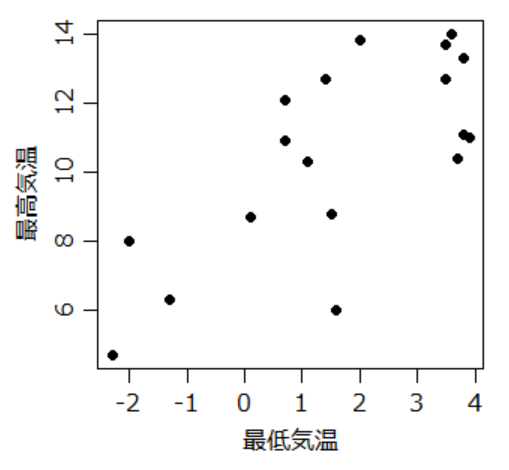
  どの日が異常っぽいというか、あまりまとまっていない…。
  
  とりあえず各日の異常度を求める。
  mu <- colMeans(cbind(x1, x2))
  xc <- cbind(x1, x2) - matrix(1, 18, 1) %*% mu
  sigma <- t(xc) %*% xc / 18
  a <- rowSums( (xc %*% solve(sigma) ) * xc)
  a <- a * (18 - 2) / ((18 + 1) * 2)
  th <- qf(df1=2, df2=18-2, 0.99)
  案の定、1%基準で異常ラインに達した日はなかった。特に寒かった15日よりも、上図においてデータ点が対角線から離れ気味の（最低気温と最高気温の差が他の日付に比べてかなり小さい）8日の方が異常度が微妙に大きかった。