2022-08-11

雑記：クリームパンにフロントドア基準を満たしてほしかった話

お気付きの点がありましたらご指摘いただけますと幸いです。

宮川雅巳. 統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学). 朝倉書店. 2004.
小麦・小麦粉の基礎知識 | 小麦粉を知る | 小麦粉百科 | レシピ・エンタメ | 日清製粉グループ

私はフロントドア基準の例として下図を考えた。つまり、小麦は薄力粉や強力粉に加工される。強力粉はパン生地に用いられる。薄力粉はカスタードクリームに用いられる。よって、カスタードクリームを包んだクリームパンでは小麦からの 2 つの異なるパスが合流することになる（ここではパン生地の原料は強力粉のみとし薄力粉は配合しないものとする）。のでフロントドア基準の例になるだろうと考えた。というか昔の記事にも意気揚々と同じ喩えを記していた。

しかし、本当にクリームパンにおいて「小麦からの 2 つの『異なる』パス」が合流するのだろうか。私は小麦粉に詳しくないが、もし薄力粉と強力粉のどちらかが他方の原料であったりしたら 2 つのパスは部分的に重なってしまい、下図の例は破綻する。そう思い調べたところ、そもそも薄力粉と強力粉は原料となる小麦の品種が異なっていた [2]。つまり、破綻していたのは「『（同一品種の）小麦』からの 2 つの異なるパス」の「同一」の方であった。私はなぜか薄力粉と強力粉というのは原料は同じ小麦だが製粉の仕方が異なるのだろうと思い込んでいたのだが、そうではなかったのである。

なので薄力粉と強力粉は共通の親をもたないことになり、「小麦」を共通の親としている下図のグラフは破綻している。無理に破綻していないようにするのであれば、もし強力粉用小麦と薄力粉用小麦が同じ肥料や同じ耕運機などを用いて生産されるならそれを共通の親にできると思われる。2 つの小麦の生産方法がほぼ同じであれば小麦生産スキル人材の人件費でもよいかもしれない。しかし、図を描き直すのが面倒なので下図の世界は同じ品種の小麦から薄力粉や強力粉が製粉できる不思議な世界であるということにする。

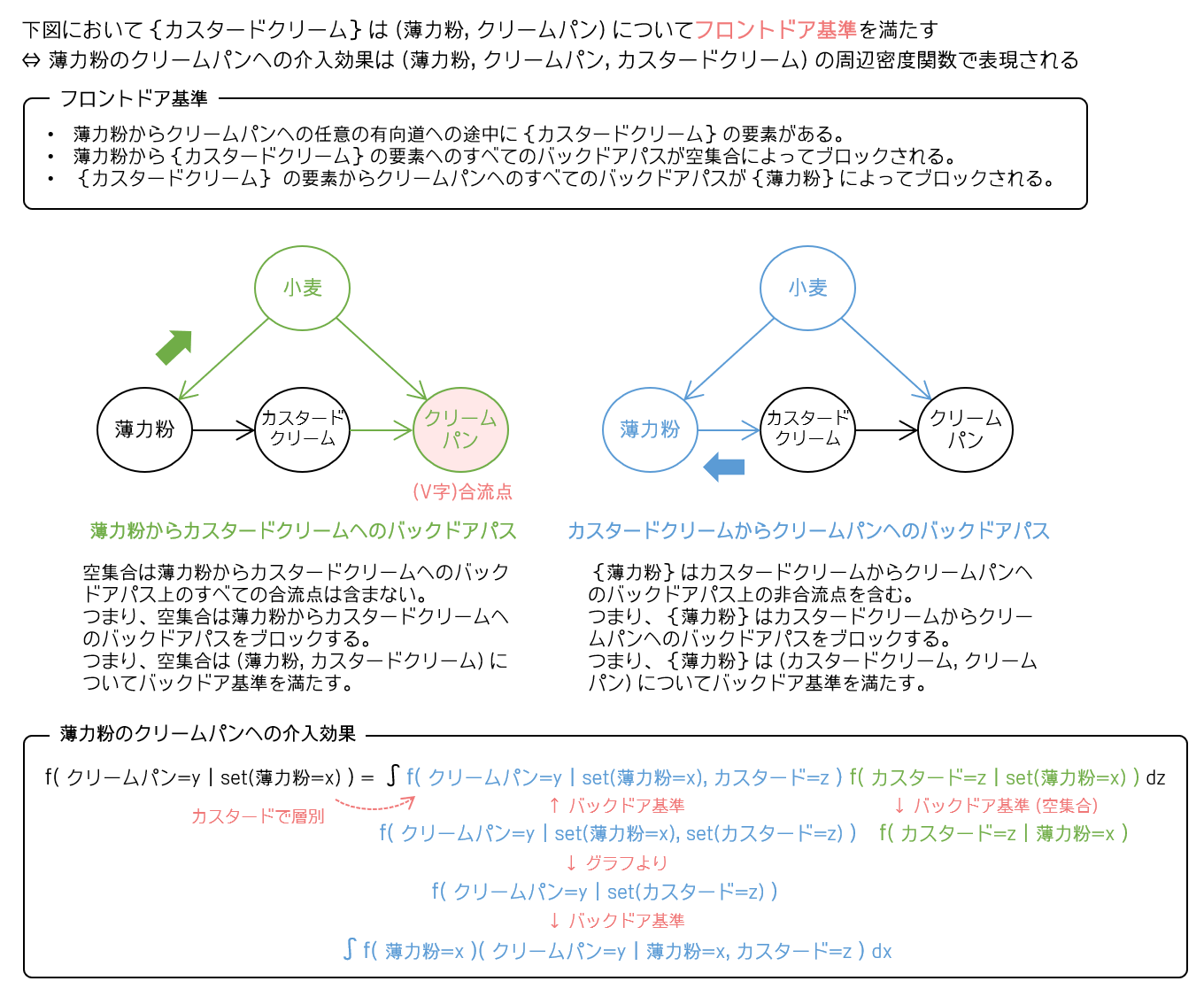
フロントドア基準の例（薄力粉と強力粉が共通の小麦から生産されるという誤った思い込みの下に描かれた）

2022-08-10

雑記

2022-08-09

雑記

お気付きの点がありましたらご指摘いただけますと幸いです。

宮川雅巳. 統計的因果推論―回帰分析の新しい枠組み (シリーズ・予測と発見の科学). 朝倉書店. 2004.

雑記 - クッキーの日記（前回）

💜

f:id:cookie-box:20211229165400p:plain:w70

前回は M 字型の非巡回的有向独立グラフに定理 4.4 と定理 4.5 を適用しましたが、W 字型も同じ要領ですね。
しかし、「｛あんパン｝を与えた下で小麦と寒天は独立か？」という問題を考えると、定理 4.5 を用いればただちに独立であることをいえますが、定理 4.4 は適用できないですよね……モラルグラフが連結グラフではなくなってしまうと思います。寒天が離れ小島になってしまうので。このとき、「｛あんパン｝は小麦と寒天を分離している」とはいわないですよね。そもそも島が離れているとこの本の「分離」の定義を適用できないと思います。まあ定理 4.4 が適用できないと感じたら定理 4.5 を適用すればよいので問題はありませんが。
70ページには「忠実」という概念が登場しますが下線が引いている文章は何をいっているのかややこしいですね……しかし、その直後に「忠実でない」具体例が説明されていますね。つまり、図 4.5 の非巡回的有向独立グラフをみると、明らかに $X_2$ と $X_3$ は独立ではないです。しかし、構造方程式の係数が奇跡のコラボレーションをすると独立になってしまうと。このようなとき、 $(X_1, X_2, X_3)$ の同時分布は非巡回的有向独立グラフに忠実ではないと。確かに忠実でないようなときは厄介なので考えたくないですね。なので忠実であると仮定してしまうと。そうすると定理 4.5 の前件が条件付独立性の十分条件から必要十分条件になりますね。
71ページには「観察的に同値」という概念も登場し、これは独立性・条件付独立性の観点でこのグラフとあのグラフが区別できない、ということですが……統計的因果探索の本では、ノイズが非ガウスのときは変数間の因果の向きが識別できるといっていましたよね。しかしここでは「ノイズが非ガウスであったらどちらのグラフか特定できるか」などといった検査はせず、「成り立つすべての独立性と条件付独立性を与えたときどちらのグラフか特定できるか」という検査をするのみなので、「特定できない」という事態になってきますね。

2022-08-08

雑記

お気付きの点がありましたらご指摘いただけますと幸いです。

https://files.core.ac.uk/pdf/2612/81864331.pdf

自由度 $n$ （ここでは $n = 1, 2, \cdots$ とする）の $t$ 分布の確率密度関数は以下である。任意の $n= 1, 2, \cdots$ についてこれを上から抑える可積分関数 $F(t)$ を考える。 $\displaystyle f_n(t) = \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} \equiv C_n \tilde{f}_n(t)$
まず、Gurland’s double inequality [1] より、任意の $n$ について以下の式が成り立つ。したがって、任意の $n$ について $C_n < 1$ が成り立つ。 $\displaystyle n \pi {C_n}^2 < \frac{n^2}{2n + 1}$
また、 $\tilde{f}_n(t)$ は以下より $\exp(-t^2/2)$ に収束するのであった。なお、この波括弧の中身は $n/t^2$ について単調増加である（証明略）。 $\displaystyle \tilde{f}_n(t) = \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} = \left( 1 + \frac{1}{n / t^2} \right)^{-1/2} \left\{ \left( 1 + \frac{1}{n / t^2} \right)^{n/t^2} \right\}^{-t^2/2} \xrightarrow[n \to \infty]{} \exp \left( - \frac{t^2}{2} \right)$ よって、 $|t| > 1$ のとき、任意の $n$ について $\tilde{f}_n(t) < 2^{-t^2/2}$ である。
他方、 $|t| \leqq 1$ のとき、 $\tilde{f}_n(t)$ は $t=0$ で最大値をとるので $\tilde{f}_n(t) \leqq 1$ である。

よって、以下の $F(t)$ は任意の $n$ について $f_n(t)$ を上から抑える。

$F(t) = \left\{ \begin{array}{ll}1 & (|t| \leqq 1)\\ 2^{-t^2/2} & (|t| > 1) \end{array} \right.$

また、 $\tilde{\tilde{f}}(t) = 2^{-t^2/2}$ は $(-\infty, \infty)$ で積分すると $\sqrt{2 \pi / \log 2}$ である。
よって $F(t)$ は可積分である。

2022-08-07

雑記

お気付きの点がありましたらご指摘いただけますと幸いです。

[1] の章末問題をやります。《要証明》の箇所は時間がなくかけていません。

2.1　 $X_n$ が自由度 $n$ の t 分布にしたがうとき、 $X_n \rightsquigarrow N(0, 1)$ であることを示せ。

$X_n$ が自由度 $n$ の t 分布にしたがうので、 $\displaystyle P(X_n \leqq x) = \int_{-\infty}^{x} \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} dt$ である（ t 分布の確率密度関数にはガンマ関数の比があらわれる）。

【解1】
[2] の Ben 氏の Answer によるとそもそもガンマ関数の比の漸近的ふるまいが [3] の Tricomi and Erdélyi, 1951 によって明らかにされており、以下となる。

$\displaystyle \frac{\Gamma(z + \alpha)}{\Gamma(z + \beta)} = z^{\alpha - \beta} \left[ 1 + \frac{(\alpha - \beta)(\alpha + \beta - 1)}{2z} + \mathcal{O}(|z|^{-2})\right]$ したがって、t 分布の確率密度関数のうちガンマ関数の比になっている部分のみの漸近的ふるまいは、 $\displaystyle \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} = \frac{1}{\sqrt{2 \pi}} \left[ 1 - \frac{1}{4n} + \mathcal{O}(n^{-2})\right]$ となり $n \to \infty$ で $1/\sqrt{2 \pi}$ に収束する。他方、確率密度関数の残りの部分も収束するので（高校で習った）、合わせると結局以下となり、右辺は標準正規分布の確率密度関数である。 $\displaystyle \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} \xrightarrow[n \to \infty]{} \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{t^2}{2} \right)$ ここで、優収束定理を用いるために、任意の自由度 $n$ の t 分布の確率密度関数がある可積分関数 $F$ で上から抑えられることを示す（証明はこちら）。よって、 $\displaystyle \begin{split} P(X_n \leqq x) &= \int_{-\infty}^{x} \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} dt \\ &\xrightarrow[n \to \infty]{} \int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{t^2}{2} \right) dt \\ &= P(X \leqq x) \end{split}$ より、 $X_1, X_2, \cdots$ は標準正規分布にしたがう確率変数 $X$ に分布収束する。ただし、1行目から2行目で極限と積分を交換するのに優収束定理を用いた。

【解2】
この問では漸近的ふるまいに興味はないので分布収束先の分布を知るには [3] のスターリングの公式を用いればじゅうぶんである《要証明》。

$\displaystyle \Gamma(z) = \sqrt{\frac{2 \pi}{z}} \left( \frac{z}{e} \right)^z \left( 1 + \mathcal{O}\left(\frac{1}{z}\right) \right)$

2.2　先の問からただちに「任意の $p \in \mathbb{N}$ について ${\rm E}X_n^p \to {\rm E}N(0, 1)^p$ である」といえるか。

ただちにはいえない。先ほどはルベーグの優収束定理を用いて極限と積分を交換できたが今回は先ほどと同じ要領で交換することはできない。 $\displaystyle {\rm E}X_n^p = \int_{-\infty}^{\infty} \frac{\Gamma \bigl( (n + 1) / 2 \bigr)}{\sqrt{n \pi} \Gamma (n / 2)} \left( 1 + \frac{t^2}{n} \right)^{-(n + 1)/2} \, t^p dt$ $\displaystyle {\rm E}N(0, 1)^p = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{t^2}{2} \right) \, t^p dt$

2.3　 $X_n \rightsquigarrow N(0, 1)$ かつ $Y_n \xrightarrow{\rm P} \sigma$ であるとき、 $X_n Y_n \rightsquigarrow N(0, \sigma^2)$ であることを示せ。

《要証明》