雑記

雑記

クロネッカー積と行列積の混合積の公式 (A \otimes B)(C \otimes D) = AC \otimes BD を成分でかいただけです．

まず，クロネッカー積は以下のように定義されると思います．

定義1（クロネッカー積）

A \in \mathbb{R}^{n_a \times m_a}, \; B \in \mathbb{R}^{n_b \times m_b} に対して A \otimes B \in \mathbb{R}^{n_a n_b \times m_a m_b} を以下のように定義する．

A \otimes B = \left( \begin{array}{cccc} a_{1,1}B & a_{1,2}B & \cdots & a_{1,m_a}B \\ a_{2,1}B & a_{2,2}B & \cdots & a_{2,m_a}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{n_a,1}B & a_{n_a,2}B & \cdots & a_{n_a,m_a}B \end{array} \right)

それで以下の公式が成り立ちます． AC \otimes BD から A, B を追放したいときなどにこれをつかうと思います．

命題1（クロネッカー積と行列積の混合積の公式）

A \in \mathbb{R}^{n_a \times m_a}, \; B \in \mathbb{R}^{n_b \times m_b}, \; C \in \mathbb{R}^{m_a \times m_c}, \; D \in \mathbb{R}^{m_b \times m_d} に対して以下が成り立つ．

(A \otimes B)(C \otimes D) = AC \otimes BD

この公式は以下のように定義にあてはめれば示せます．

命題1の証明0（ブロックごとに行列積をとる）

\begin{split} (A \otimes B)(C \otimes D) &= \left( \begin{array}{cccc} a_{1,1}B & a_{1,2}B & \cdots & a_{1,m_a}B \\ a_{2,1}B & a_{2,2}B & \cdots & a_{2,m_a}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{n_a,1}B & a_{n_a,2}B & \cdots & a_{n_a,m_a}B \end{array} \right) \left( \begin{array}{cccc} c_{1,1}D & c_{1,2}D & \cdots & c_{1,m_c}D \\ c_{2,1}D & c_{2,2}D & \cdots & c_{2,m_c}D \\ \vdots & \vdots & \ddots & \vdots \\ c_{m_a,1}D & c_{m_a,2}D & \cdots & c_{m_a,m_c}D \end{array} \right) \\ &= \left( \begin{array}{cccc} \sum_{k=1}^{m_a} a_{1,k} c_{k,1} BD & \sum_{k=1}^{m_a} a_{1,k} c_{k,2} BD & \cdots & \sum_{k=1}^{m_a} a_{1,k} c_{k,m_c} BD \\ \sum_{k=1}^{m_a} a_{2,k} c_{k,1} BD & \sum_{k=1}^{m_a} a_{2,k} c_{k,2} BD & \cdots & \sum_{k=1}^{m_a} a_{2,k} c_{k,m_c} BD \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{k=1}^{m_a} a_{n_a,k} c_{k,1} BD & \sum_{k=1}^{m_a} a_{n_a,k} c_{k,2} BD & \cdots & \sum_{k=1}^{m_a} a_{n_a,k} c_{k,m_c} BD \end{array} \right) \\ &= AC \otimes BD \end{split}


完全に上の証明でいいんですが，より明示的に成分が等しいことに基づく証明もしておきたい気がします．なので，クロネッカー積の定義を成分にかき直します．ちなみに後で気付いたんですが，ここで「これ以降行列のインデックスをゼロ始まりでとることに決める」と宣言しておけばよかったです．以降では右肩に (0) を付けたときにゼロ始まりのインデックスでとるとしていますが証明では全部右肩に (0) が付いています．無駄です．

定義1'（クロネッカー積の成分；通常のインデックスでアクセス）

x を超えない最大の整数を {\rm floor}(x)，x を y で割った余りを {\rm mod}(x,y) とかくと，A \otimes B の i, \, j 成分は以下のようにかける（ 1 \leqq i \leqq n_a n_b， 1 \leqq j \leqq m_a m_b ）．

(A \otimes B)_{i,j} = a_{\, {\rm floor} ( (i-1) /n_b)+1, \, {\rm floor} ( (j-1) /m_b )+1 \, } b_{\, {\rm mod}( (i-1), n_b) + 1, \, {\rm mod}((j-1), m_b) + 1\, }

以降，表記の便利のため，右肩に (0) を付けたときはゼロ始まりのインデックスで成分をとることにする．すると以下のようになる（ 0 \leqq i' \leqq n_a n_b - 1， 0 \leqq j' \leqq m_a m_b- 1 ）．

(A \otimes B)^{(0)}_{i',j'} = {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, {\rm floor} ( j'/m_b ) \, } {b}^{(0)}_{\, {\rm mod}(i', n_b), \, {\rm mod}(j', m_b) \, }

上の定義でクロネッカー積の成分にアクセスできると思うんですが，{\rm floor} や {\rm mod} が多用されていてみづらいという声もあると思うので最初から {\rm floor} と {\rm mod} の2重インデックス（行と列があるので4重インデックス）でアクセスする方法も用意します．

定義1''（クロネッカー積の成分；大インデックスと小インデックスでアクセス）

A \otimes B の n_b I' +i, \, m_b J' + j 成分は以下のようにかける（ 0 \leqq I' \leqq n_a - 1， 0 \leqq J' \leqq m_a - 1， 1 \leqq i \leqq n_b， 1 \leqq j \leqq m_b ）．

(A \otimes B)_{\, n_b I' + i, \, m_b J' + j \,} = a_{\, I' + 1, \, J' + 1 \, } b_{\, i, \, j \, }

ゼロ始まりのインデックスだと以下のようになる（ 0 \leqq i' \leqq n_b - 1， 0 \leqq j' \leqq m_b- 1 ）．

(A \otimes B)^{(0)}_{\, n_b I' + i', \, m_b J' + j' \,} = a^{(0)}_{\, I', \, J' \, } b^{(0)}_{\, i', \, j' \, }

それで定義1' のアクセス方法で命題1を証明すると以下になります．{\rm floor} と {\rm mod} のせいで横幅が長くなってしまうことがわかります．

命題1の証明1（定義1' を使用）

0 \leqq i' \leqq n_a n_b - 1， 0 \leqq j' \leqq m_c m_d - 1 について，以下が成り立つ．

\begin{split} \displaystyle \bigl( (A \otimes B)(C \otimes D)\bigr)^{(0)}_{i',j'} &= \sum_{k'=0}^{m_a m_b - 1} {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, {\rm floor} ( k'/m_b ) \, } {b}^{(0)}_{\, {\rm mod}(i', n_b), \, {\rm mod}(k', m_b) \, } {c}^{(0)}_{\, {\rm floor} (k'/m_b), \, {\rm floor} ( j'/m_d ) \, } {d}^{(0)}_{\, {\rm mod}(k', m_b), \, {\rm mod}(j', m_d) \, } \\ &= \sum_{k'=0}^{m_a m_b - 1} \Bigl( {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, {\rm floor} ( k'/m_b ) \, } {c}^{(0)}_{\, {\rm floor} (k'/m_b), \, {\rm floor} ( j'/m_d ) \, } \Bigr) \Bigl( {b}^{(0)}_{\, {\rm mod}(i', n_b), \, {\rm mod}(k', m_b) \, } {d}^{(0)}_{\, {\rm mod}(k', m_b), \, {\rm mod}(j', m_d) \, } \Bigr) \\ &= \sum_{k'=0}^{m_b - 1} \Bigl( {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, 0 \, } {c}^{(0)}_{\, 0, \, {\rm floor} ( j'/m_d ) \, } \Bigr) \Bigl( {b}^{(0)}_{\, {\rm mod}(i', n_b), \, k' \, } {d}^{(0)}_{\, k', \, {\rm mod}(j', m_d) \, } \Bigr) \\ & \quad \, + \sum_{k'=0}^{m_b - 1} \Bigl( {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, 1 \, } {c}^{(0)}_{\, 1, \, {\rm floor} ( j'/m_d ) \, } \Bigr) \Bigl( {b}^{(0)}_{\, {\rm mod}(i', n_b), \, k' \, } {d}^{(0)}_{\, k', \, {\rm mod}(j', m_d) \, } \Bigr) \\ & \quad \, + \cdots + \sum_{k'=0}^{m_b - 1} \Bigl( {a}^{(0)}_{\, {\rm floor} (i'/n_b), \, m_a-1 \, } {c}^{(0)}_{\, m_a-1, \, {\rm floor} ( j'/m_d ) \, } \Bigr) \Bigl( {b}^{(0)}_{\, {\rm mod}(i', n_b), \, k' \, } {d}^{(0)}_{\, k', \, {\rm mod}(j', m_d) \, } \Bigr) \\ &= \left( \sum_{k''=0}^{m_a - 1} {a}^{(0)}_{\, {\rm floor} (i'/n_b) , \, k'' \,} {c}^{(0)}_{\, k'', \, {\rm floor} ( j'/m_d ) \,} \right) \left( \sum_{k'=0}^{m_b - 1} {b}^{(0)}_{\, {\rm mod}(i', n_b), \, k' \,} {d}^{(0)}_{\, k', \, {\rm mod}(j', m_d) \,} \right) \\ &= (AC)^{(0)}_{\, {\rm floor} (i'/n_b), \, {\rm floor} ( j'/m_d ) \, } (BD)^{(0)}_{\, {\rm mod}(i', n_b), \, {\rm mod}(j', m_d) \, } \\ &= (AC \otimes BD)^{(0)}_{i',j'} \end{split}

以上より， (A \otimes B)(C \otimes D) = AC \otimes BD である．□

他方，定義1'' のアクセス方法で命題1を証明すると以下になります．横幅が短いです．また，後から気付いたんですが以下のように右辺から出発した方が（2重ループを1重ループにまとめる方向になるので）すっきりする気がします．

命題1の証明2（定義1'' を使用）

0 \leqq I' \leqq n_a - 1， 0 \leqq J' \leqq m_c - 1， 0 \leqq i' \leqq n_b-1， 0 \leqq j' \leqq m_d-1 について，以下が成り立つ．

\begin{split} \displaystyle (AC \otimes BD)^{(0)}_{\, n_b I' +i', \, m_d J' + j' \,} &= \left( \sum_{k=0}^{m_a - 1} a^{(0)}_{\, I', \, k \,} c^{(0)}_{\, k, \, J' \,} \right) \left( \sum_{k'=0}^{m_b - 1} b^{(0)}_{\, i', \, k' \,} d^{(0)}_{\, k', \, j' \,} \right) \\ &= \sum_{k=0}^{m_a - 1} \sum_{k'=0}^{m_b - 1} \Bigl( a^{(0)}_{\, I', \, k \,} b^{(0)}_{\, i', \, k' \,} \Bigr) \Bigl( c^{(0)}_{\, k, \, J'\,} d^{(0)}_{\, k', \, j' \,} \Bigr) \\ &= \sum_{k=0}^{m_a - 1} \sum_{k'=0}^{m_b - 1} (A \otimes B)^{(0)}_{\, n_b I' +i', \, m_b k + k' \,} (C \otimes D)^{(0)}_{\, m_b k +k', \, m_d J' + j' \,} \\ &= \sum_{K=0}^{m_a m_b - 1} (A \otimes B)^{(0)}_{\, n_b I' +i', \, K \,} (C \otimes D)^{(0)}_{\, K, \, m_d J' + j' \,} \\ &= \bigl( (A \otimes B) (C \otimes D) \bigr)^{(0)}_{\, n_b I' +i', \, m_d J' + j' \,} \end{split}

以上より， (A \otimes B)(C \otimes D) = AC \otimes BD である．□

おまけ

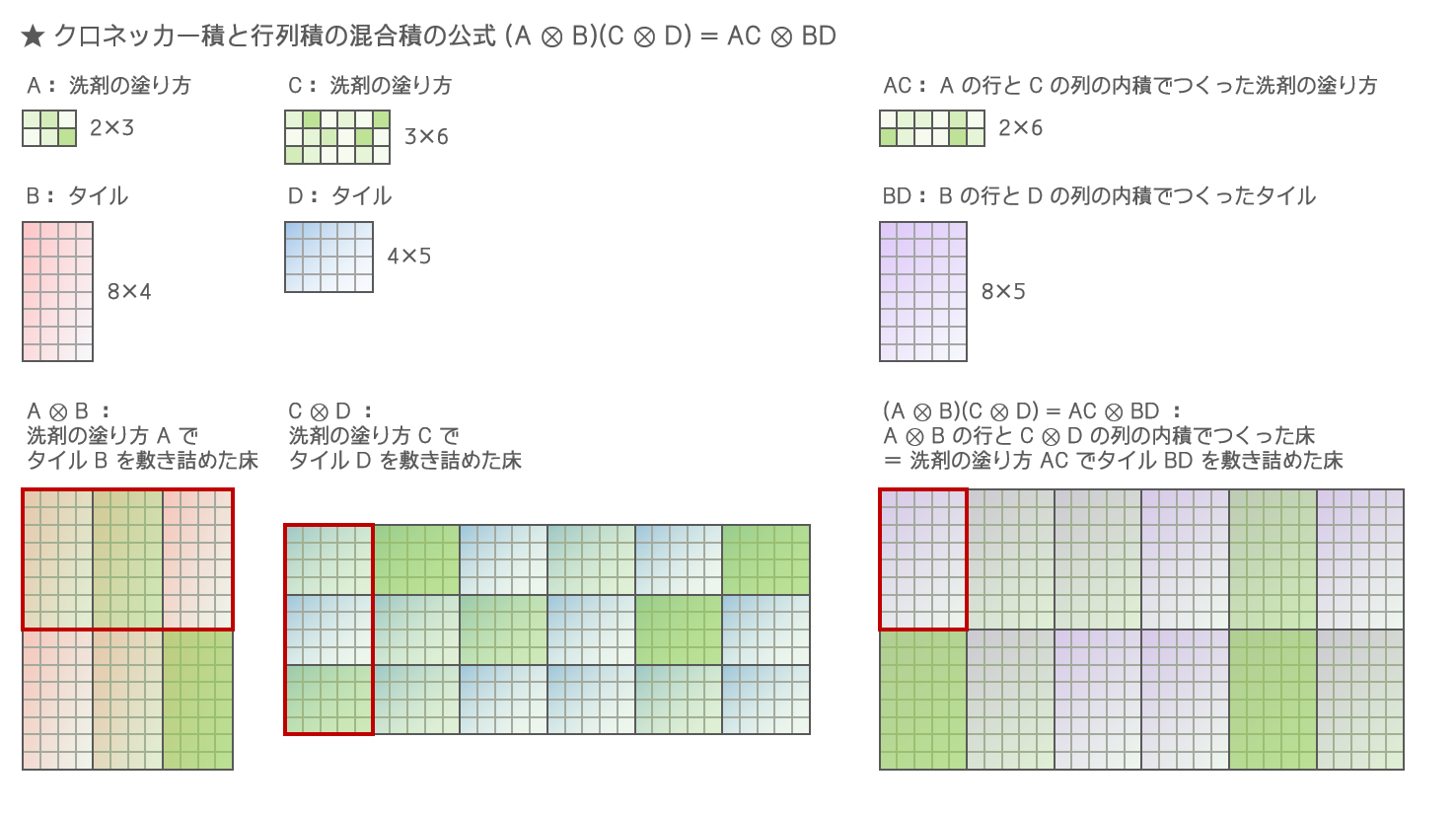
クロネッカー積と行列積の混合積のイメージ図を描きました．クロネッカー積をとることは洗剤を指定の濃さに塗りながらタイルを敷き詰めることに似ていると思ったのですが，いうほど洗剤を塗りながらタイルを敷き詰めることをするかというとしないので完全に駄目です．
f:id:cookie-box:20210329190053p:plain