RNN を進化戦略で最適化する話（準備）

お気付きの点がありましたらご指摘いただけますと幸いです。

Paul Vicol, Luke Metz, Jascha Sohl-Dickstein. Unbiased Gradient Estimation in Unrolled Computation Graphs with Persistent Evolution Strategies. In Proceedings of the 38th International Conference on in Machine Learning (ICML 2021), 2021.
Unbiased Gradient Estimation in Unrolled Computation Graphs with Persistent Evolution Strategies
進化戦略 - Qiita

f:id:cookie-box:20210810231537p:plain:w60

ICML2021 の Outstanding Paper Award が Unbiased Gradient Estimation in Unrolled Computation Graphs with Persistent Evolution Strategies ―パーシステント進化戦略を用いた展開計算グラフの最適化というようなタイトルでしたが…展開計算グラフというのは、RNN のように、入力（系列）から出力（系列）をつくるときに同じ重みパラメータを何度も使うネットワーク構造などですよね（下図）。

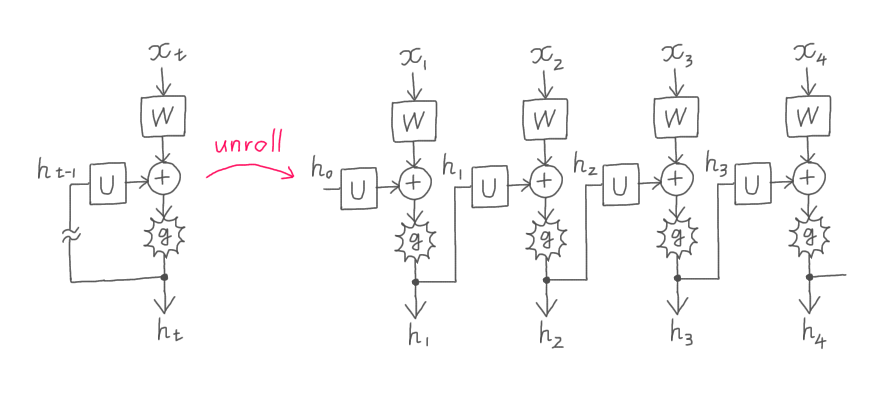
f:id:cookie-box:20210819145415p:plain:w540

アブストラクトによると、「このようなグラフの学習は勾配のバリアンスが大きくなり、バイアスが生じ、更新にも時間がかかり、メモリも要する」などとありますが、バリアンスが大きいというのは何がいいたいのでしょうか？バイアス‐バリアンスというのはモデルのアンサンブルの文脈でよく聞く誤差の期待値の分解ですよね？バイアスというのは考えるモデルがどこまで真のモデルに迫れるかの期待値で、バリアンスというのはデータなどを変えて学習を繰り返したときのぶれやすさで、バリアンスが大きいモデルであればアンサンブル平均すれば誤差の期待値を抑える余地があるというような。

雑記：モデルをアンサンブルしたい話（その1―カステラ本7.3節、8.7節） - クッキーの日記

しかし、RNN はアンサンブルモデルではないですよね。バリアンスを取り沙汰すことに何の意味が？それも勾配の？

f:id:cookie-box:20210810231543p:plain:w60

そもそも RNN で勾配のバリアンスが大きくなりやすいというのは、同じパラメータで1ステップ目、2ステップ目、3ステップ目、…、現在のステップの入力データをすべて捌かなければならないことをいっているのかな？あまり本文中に詳しくかいていないようにみえるけど。RNN だと、あるパラメータを更新すべき方向が、現在のステップに対するのと1つ前のステップに対するのとで逆にもなりうるよね。だから再帰構造をもたないネットワークより学習が不安定になりがちで、ゆえに期待バイアスも大きいという雰囲気なのかな？学習が不安定かとかは学習のアルゴリズムにも依存する話だけど。

まあそれで、部長のいう通り RNN はアンサンブルモデルではないよね。展開されたモデルをみると同じモデルが並んでいて少しアンサンブルのような雰囲気を感じるけど、もし展開されたモデルたちのパラメータが同期されていなかったらそれはもはや RNN ではないしね。でも、それは学習済みの RNN を眺めたときの話だよね。RNN を学習する過程に工夫の余地はないかな？ということが続きにかかれていると思うんだけど。

え？えっと、アブストラクトの続きによると、RNN にはその勾配のバリアンスなどの課題があるので、パーシステント進化戦略（PES: Persistent Evolution Strategies）なる方法を導入したようです。つまり、展開したモデルを分割し、進化戦略で更新していく…進化？？

分割するってことは、本当は同じ重みパラメータを一旦は別々のものと考えるんだと思う。そうすると分割した数だけパラメータの勾配方向が生成されてしまうけど、進化戦略というからそれらを遺伝子たちだと考えて最良な固体を探していくのかな…という方法かは中身を読まないとわからないけど、もしそうなら勾配のアンサンブルだから通常の分割しない最適化と違ってバリアンスを抑制できるよね。進化戦略（ES）は遺伝的アルゴリズム（GA）とよく似ていて、組み換えや突然変異を起こしてベクトルを最適化していく方法だね（正確には ES と GA は異なる系譜の手法だけど）。

えっこれそんな論文なんですか？遺伝的アルゴリズムというと、あのいかがわしい画像を生成する？

そういう使い方もあるけれども。

とりあえず進化させることで系列タスクに対する既存手法よりもバリアンスもバイアスも抑制でき、パラメータの更新が高速になり、メモリも要さないと…あれ、既存手法ってそもそもどうやってパラメータを更新するんでしたっけ？？

RNN のパラメータを学習する既存手法は論文の4枚目の表に色々あるね。その表の1行目にもあるように基本的には BPTT（backpropagation through time）を用いるよ。BPTT というのは…下のスライドで時刻 $t$ に $L_t$ という損失が発生しているよね。これを小さくしたいとき、ネットワークの重みのうち $V$ はスライド中の (9.3) の勾配で更新していいんだけど、 $U$ と $W$ についてはスライドの一番下の行の勾配で更新するのでは不十分なんだよね（※）。

※ スライドの記述が不明瞭ですが、一番下で「 $L_t$ の $W, U$ に関する勾配」といっているのは「 $L_t$ を図の $x_t, h_{t-1}, W, U$ の関数とみなしたときの $W, U$ に関する勾配」です。

なぜなら、実は $h_{t-1}$ は $U$ と $W$ に依存しているからね（このスライドの図が展開になっていなくてあれだけどこのグラフが左にずっと繰り返されるよ）。

ああっ確かに $U$ と $W$ をずらすと $h_{t-1}$ もずれてしまうはずですよね。 $L_t$ を減らそうとして $U$ と $W$ をずらしたのに $h_{t-1}$ までずれてきたら意味がありません。いったいどうすれば…。

だから上記の現在の勾配に加えてもっと時刻をさかのぼっていって、ここに至るまでの時刻の $h_{t'} \; (t'=\cdots, t-1)$ に関する勾配も求めて、 $U$ と $W$ はそれらすべての和で更新する。それが BPTT。

えっ BPTT ってそれだけなんですか？いやでもそれがシンプルなんでしょうか。実際にはある時刻での勾配はその時刻以降の隠れ層に影響してしまうので、単純な和が最適な更新方向にはならなさそうですが…。

うん。ちなみに「更新にも時間がかかり、メモリも要する」というのもこのすべての勾配を求めていくことに起因しているよ。ここに至るまでのすべての時刻での隠れ層の値を記憶しておかなければすべての勾配が出せないし、並列処理もできなくて時間がかかる。それで RTRL（real-time recurrent learning）という手法が提案された。現在発生している誤差に対する勾配をみて、次の時刻の入力を受ける前にパラメータを更新してしまうという手法だね。でも入力を受け取る度にいちいちパラメータを更新していく分、計算量が膨れ上がる。だから近似的に RTRL を実現できないかというのがその後の研究の主流だったみたいだけど、それでも実装が複雑だったり、バリアンスを抑えられなかったり、特定のクラスの損失にしか適用できなかったりするとある。

そうですね、その RTRL でもパラメータを逐次更新にはしているものの、結局は各時刻の損失に対しての最適化を重ねているだけなので、更新方向の不安定さに根本的に立ち向かっているようにはみえません。

その問題に多少切り込んだ先行研究もあって、それが「進化戦略（ES: evolution strategies）によるスムージング」なのかな。ES では直接勾配を求めない。確率的有限差分（stochastic finite-differences）を用いるというようにあって、確率的に更新方向を探索して蓄積していくんだね。よくある正則化のように学習の安定化を図る効果があるんだと思う。これが実際上手くいくケースもあるらしい。ただ長い入力系列の学習にはやはり計算コストが高いから、入力長を足切りするしかなく、それがバイアスにつながると。

計算コストのために入力長を足切りするというのは、それはもう常にそうせざるを得ないのではないですか？それでバイアスが生じるといわれても。というか、今回の手法も展開モデルを分割するとかいっていませんでしたっけ？

うん。だけど、今回の手法、PESではそれぞれの分割でどの方向を探索したかを蓄積することで、バイアスを抑えられるらしい。具体的なアルゴリズムをみてみよう。6ページ目だね。

はあ。まず右側が先行手法の ES ですね。

つづいたらつづく