Skype数学勉強会 確率論セミナー の参加メモ
読んでいる本: はじめての確率論 測度から確率へ : 佐藤 坦 : 本 : Amazon
今日読んだ範囲: 174~176ページ
記事タイトルのカッコ内の数字は、ウィキに合わせて休講もカウントした回数にしました。
以下雑多なメモ。
- 収束列: 収束先の
がある。
- コーシー列:
- 収束列はコーシー列: 収束列だったら収束先の
があってその
近傍に全部入る。
- 完備距離空間: コーシー列が収束する距離空間
。
- 実数
は完備。
が完備じゃなくても部分集合
は完備になりえる。
はいつも完備。コーシー列がないから。
- ( (0, 1], 普通の距離 ) は完備じゃない。0に近づくコーシー列が収束しないから。
- なお、距離
を以下の赤線のようにすれば完備になる。0に近づくコーシー列がないから。
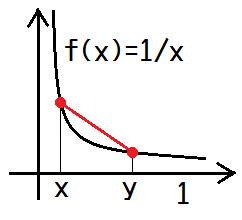
- なお、距離
- 実数
- 前回やった、数列と数列の間に距離をいれたやつは完備。
(数列がずれはじめる最初のインデックスを用いて
を距離とする。)
- イメージ:
- ある数列とある数列の距離が 1/2 未満だったら、1項目まで同じ。
- ある数列とある数列の距離が 1/4 未満だったら、2項目まで同じ。
- ある数列とある数列の距離が 2^(-N) 未満だったら、N項目まで同じ。
- 数列のコーシー列があったら、数列の各項に極限がある。
- 証明:
が数列の空間
のコーシー列であるとする。
- コーシー列なので、
番目から互いの距離が
未満になる。→
番目以降1項目は同じ。
- コーシー列なので、
番目から互いの距離が
未満になる。→
番目以降2項目まで同じ。
- コーシー列なので、
番目から互いの距離が
未満になる。→
番目以降
項目まで同じ。
- この同じになっていく先を
とおく。これが
の収束先であることを示す。
- 収束することを示すので
をとる。
であるような
をとる。
の
番目以降は
項目まで
と同じ。
- k項目まで
と同じなのだったら、
との距離が
未満。
未満。
の
番目以降
との距離が
未満なので、
は
に収束する。
- イメージ: