参考文献:経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) | 沖本 竜義 | 本 | Amazon.co.jp
参照データ:【日経平均株価】株価指数 時系列データ 日足
R tseries の garch をつかってみる。GARCH モデルについては参考文献の7章を参照。見せかけの回帰は考慮していません。本記事(というより全記事)の内容には誤りを含む可能性があります。
前置き
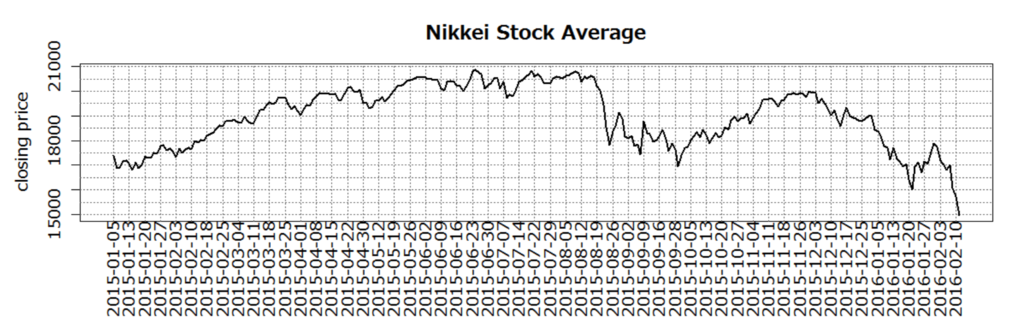
- 対数差分系列(≒微小期間の収益率)にする。この系列の全期間平均は -0.0006 なので、0 と考える。
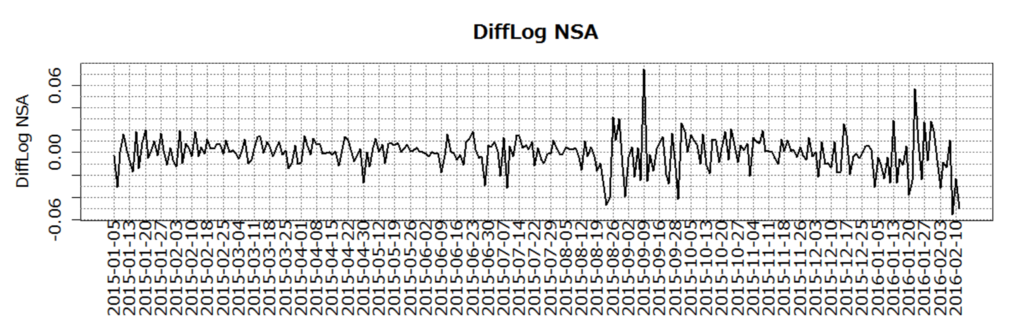
- 対数差分系列の自己相関係数、偏自己相関係数もプロットする。
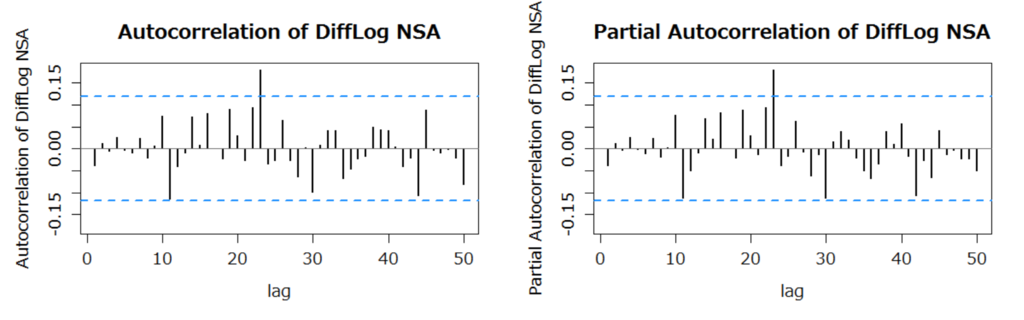
- 水色の破線は、各時点のデータが互いに独立でかつ同一の分布であると仮定したときに、帰無仮説「自己相関係数=0」が対立仮説「自己相関係数≠0」に対して有意水準5%で棄却される点(参考文献の15ページ参照)。
- 1~50次の自己相関係数がほぼこのライン内にあるので、日経平均株価の対数収益率を y_t = 0 + u_t(u_t は残渣)でモデル化することは、対数収益率の期待水準(0だけど…)を表現する上で変ではない。
(もし残渣に自己相関があったら、モデルが対数収益率の期待水準がもつ自己相関を表現できていない。)
- ただし、対数差分系列をみると「5月下旬~6月頭はあまり分散がない」「9月は分散が大きい」などという性質があり、上のモデルは明らかにこの性質を表現できていない。特に金融データでは期待水準だけでなく期待分散にも興味があるので、このような性質が表現できてほしい。
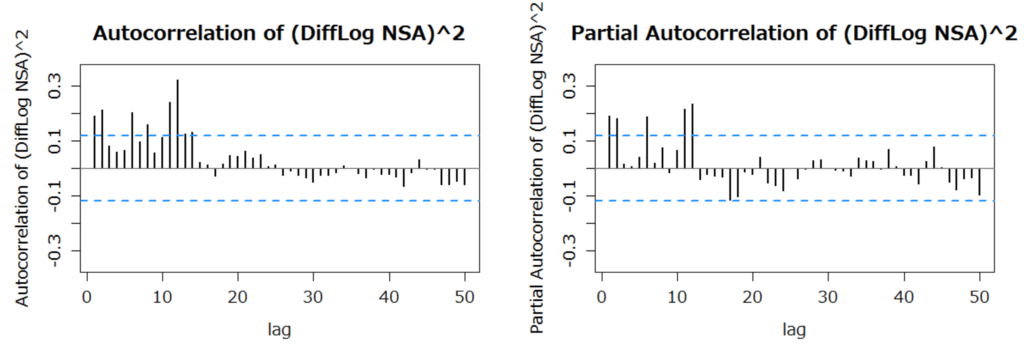
- 実際、対数差分系列の2乗の自己相関係数、偏自己相関係数は、0である帰無仮説が棄却される域にある(下図)。
- そこで、モデルを y_t = 0 + √h_t * v_t (h_t が分散のモデルで、v_t は誤差の調整)としたい。
ここから GARCH の話
- GARCH の考え方: あるステップの条件付き分散(h_t)が、前ステップまでの条件付き分散(h_{t-1}, h_{t-2}, ...)と、前ステップまでの系列の2乗(y_{t-1}^2, y_{t-2}^2, ...)の線形和でかける。
- それぞれ何ステップ前までつかうかは、割と1ステップでよいらしい = GARCH(1,1)。
- 正確には y_t ではなく y_t - μ_t の2乗をつかう。今回は μ_t ≡ 0 と考えている。
- 上で前ステップの条件付き分散をつかわないバージョンが ARCH。ARCH は次数が大きくなりやすい。
- 今回の対数差分系列に対して garch をコールすると以下のようになる(出力は中略)。
- つまり、今回の対数差分系列を GARCH(1,1) で表すなら、あるステップの条件付き分散は、前ステップの実現値の2乗の 0.17 倍と、前ステップの条件付き分散の 0.81 倍の和とするのが一番もっともらしいと。
> library(tseries)
> garch(x)
Coefficient(s):
a0 a1 b1
7.293e-06 1.735e-01 8.074e-01
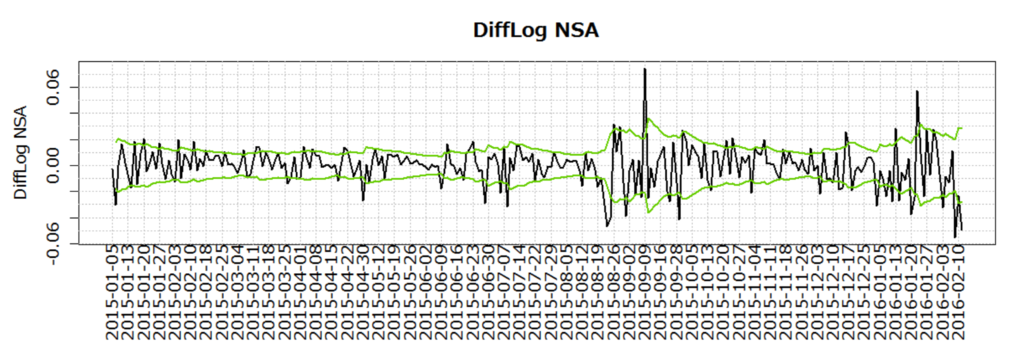
- 上記の結果(garch をコールした返り値に含まれている)を元データに重ねてプロットすると以下。
- 「5月下旬~6月頭はあまり分散がない」「9月は分散が大きい」などを表現できている。
- 次に検証すべきこと(がこれでじゅうぶんかはあやしい)。
- 標準化残渣 v_t = u_t / √h_t およびその2乗は自己相関をもたないか。
- もしもっていたら、√ht は差分系列の分散の自己相関をじゅうぶん表現できていない or やりすぎ。
- 標準化残渣 v_t = u_t / √h_t およびその2乗は自己相関をもたないか。
- 確かめると、標準化残渣及びその2乗の自己相関はないといえる。
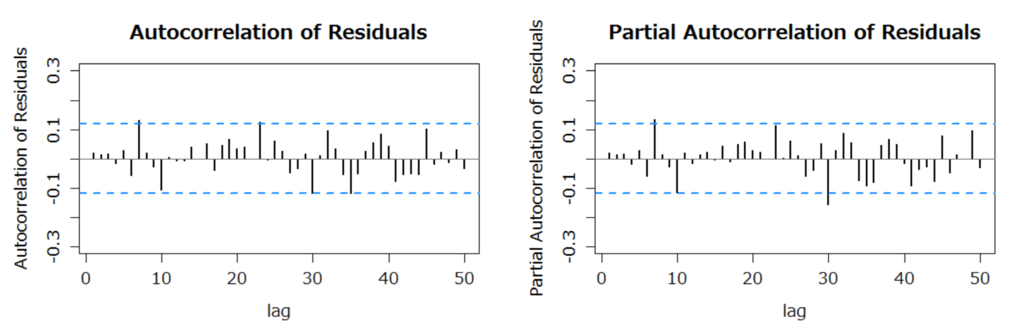
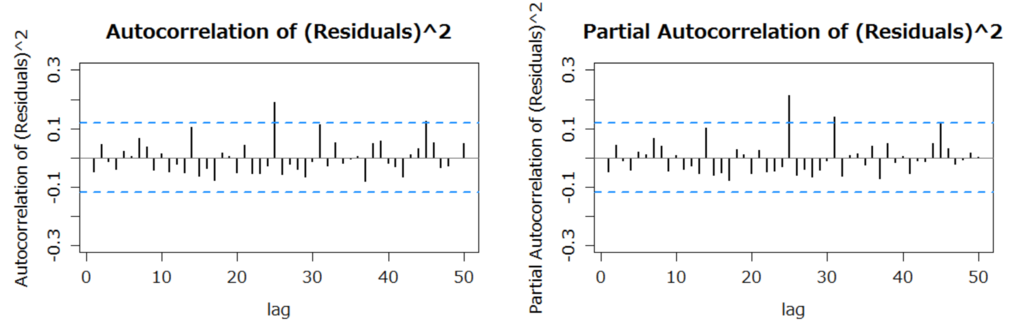
- では、このモデルが上記の期間より先も有効なのか。→ データを分割すれば何かできるが、割愛。
- 最後に、GARCH には以下のような限界がある。→ これらを克服するための GARCH の修正は参考文献の7章。
- h_t > 0 の保証のためにパラメータに制約が必要。
- 分散の変動と期待値の変動が相互作用しない。
- 差分系列の正方向への変動も負方向への変動も、分散に及ぼす影響が対称なため、明らかにレバレッジ効果(負方向への変動の方が分散により大きな影響をもたらす傾向)を表現できない。