2019-01-04

Reinforcement Learning: An Introduction〔Second Edition〕（その1）

以下の本を読みます。何かお気付きの点がありましたらご指摘いただけますと幸いです。
Sutton & Barto Book: Reinforcement Learning: An Introduction

〈参考〉過去に強化学習についてかいたものへのリンク

次回：まだ

f:id:cookie-box:20190101155733p:plain:w60

なぜかうちの部には活動費がちっとも配分されなかったので、当面の部活は無料の書籍で勉強したいと思うんです。そこで何かないか探したところ、ネットで上の Full Pdf を見つけて。何でもこの強化学習という分野は現実の問題への応用も目覚ましく、中にはベイズ的な解法もあるとか…。

f:id:cookie-box:20190101160814p:plain:w60

去年の11月に出た本なんだ。原著だから英語だね。部長は英語読める？

さして読めませんね。この前の定期テスト、英語は追試でした。

追試て。うちの部に予算下りなかったの部長の成績不良が原因なんじゃ…。

しかし安心してください。この本の第1版は邦訳（以下）が出ており、幸いそれが手元にあるので適宜内容を照らし合わせながら読むことができ…ってあれ？目次が結構違う…。

強化学習

作者: Richard S.Sutton,Andrew G.Barto,三上貞芳,皆川雅章
出版社/メーカー: 森北出版
発売日: 2000/12/01
メディア: 単行本（ソフトカバー）
購入: 5人クリック: 76回
この商品を含むブログ (29件) を見る

原著の第1版は1998年…ちょうど20年前なんだね。20年も経ったら目次も変わるんじゃないかな。

というわけで、副部長の英語力に頼らざるをえず。

Google翻訳とかあるんだから部長も頑張ってくんないかな…第1版もあるなら、まず目次の変化から見てみてもいいかもね。まず部長の持っている第1版の邦訳版だけど、以下の3部構成だね。

I. 強化学習問題
II. 基本的な解法群
III. 統一された見方

まず第I部で「強化学習」といわれる問題の枠組みとは何かと、その様々な解法に共通の概念を導入している。第II部で基本的な3つの解法を紹介、第III部ではそれらの解法をどんどん統一していっている。対して最新の第2版は、やっぱり3部構成なんだけどその内訳が違うね。

I. Tablar Solution Methods（テーブル形式の解法群）
II. Approximate Solution Methods（近似的な解法群）
III. Looking Deeper

第1版において第1部を割かれていた「強化学習とは何か」は第一部より前に「導入」という1章で片付けられているね。この20年で人々に「コンピュータが学習するということ」を説明する障壁が下がったから…かどうかは知らないけどね。というよりは、第1版で「強化学習とは何か」に含まれていた「マルコフ決定過程」という内容が「テーブル形式の解法群」の話の方に移動しただけなのかな。第2版の第I部は、「テーブル形式の解法群」というタイトルで、概ね第1版の第II部に相当するけど、第1版では第III部に含まれていた内容の一部もここに含まれているね。第2版の第II部は「近似的な解法群」で、第I部で近似ではない解法を学んでからじゃあ次は近似解法って流れかな。第III部は色々なトピックがあるけど最初の方は動物の学習とのアナロジーを論じているのかな…なんか神経細胞の絵とかあるし…。第1版と同様最後にはケーススタディと強化学習の最新の応用の話もあるね。

Solution Methods、解法群…この本には解法がたくさん載っているということですか？この手の本というのは、例えば章ごとに色々なモデルが紹介されていて、モデルと一緒にその解法がかかれているのではないんですか？有名なPRMLも、「第3章線形回帰モデル」「第4章線形分類モデル」「第5章ニューラルネットワーク」…というようになっていますよね。こちらの本は、解法ばかりなんですか？ 1つのモデルの解法がそんなにあるんですか？？

…それはちょっと出発点が違うんじゃないかな。部長がイメージしている「解法」って、「モデルを決めた後、その未知パラメータを決定する方法」だよね？その文脈で「解法が複数ある」っていうのは、同じモデルのパラメータを決定するのでも、異なる損失関数（2乗誤差とか交差エントロピーとか※）や最適化アルゴリズム（SGD とか AdaGrad とか Adam とか）がありうるみたいなものだよね。でも、現実に目の前の問題を解こうとするとき、普通はそもそも「どのモデルを使うか」から考えないといけないんじゃないかな。だから、そういう意味ではモデルを選ぶところから含めて「解法」になると思う。そう考えればそのPRMLの第3, 4, 5章だって、全部「入力に対して正しい出力を予測する問題」の解法だよね（正解ラベル付きの訓練データを使った）。それぞれ「線形モデルで回帰する解法」「線形モデルで分類する解法」「ニューラルネットワークを用いた解法」といえる。もっというとその「訓練データを使って未知の入力に対する出力を予測する問題」を解くことを総じて「教師あり学習」というよね。

※	厳密な見方をすれば、損失関数を変えたらもはや解いている問題が違うという見方もあるかもしれません。

なるほど、ここでいっている「解法」はどこから解くかの出発点が違う…コミケは会場に到着する前から既に始まっているということなんですね。

全然違うかな。りんかい線や付近住民に迷惑は掛けないでほしいかな。

となると、この本の「解法」たちはどのような問題に対する解法なんでしょうか。

だからそれが「強化学習問題」で、それが何かをこれから読んでいくんだけど…本文に入ると、序文では、この20年で計算機の処理能力の向上に牽引されて人工知能分野は凄まじい発達を遂げたとあるね。この本では強化学習の中心的なアイデアやアルゴリズムを紹介するけど、第1版同様本の位置付けはあくまでイントロダクションで、あとオンライン学習のアルゴリズムに焦点を当てているらしい。第2版では近年重要になってきたトピックも紹介するけど、包括的な説明ではないって。あと数学的に厳密な議論は第1版同様避けているけど、トピックをより深く理解するために必要なときはスキップもできるように網掛けのボックスで取り上げているって。38～40ページのような箇所がそれなのかな。あ、あと序文内に表記の定義もあるね。第1版から変更された表記もあるらしい。まず確率変数は大文字で、その実現値を小文字でかくことに統一するって。ステップ $t$ における「状態」「行動」「報酬」が $S_t, \, A_t, \, R_t$ で、それらがどんな値をとったかが $s,\, a, \, r$ というようにね。

ちょっと待ってください、「状態」「行動」「報酬」…？強化学習は状態空間モデルと関係あるんですか？それにしても「行動」と「報酬」というのはいったい…？

状態空間モデルにおける「状態」と強化学習における「状態」は違う。状態空間モデルにおける「状態」は、「（一般に）時間変化する変数で、直接観測できないので、観測できる変数から推定したいもの」だけど、強化学習における「状態」は「時間変化する変数で、それを毎ステップ観測して、それがどんな値かに基づいて行動を選択するのにつかうもの」だね。「環境」からのシグナルといってもいい。…もう面倒だからネタバレになるけど第1版に基づいた絵を下に貼っておくよ（ただし第2版の表記にならって確率変数を大文字に変えてあるよ）。

f:id:cookie-box:20190104172718p:plain:w620

大雑把にいうと、強化学習問題とは「毎ステップ適切な行動を選択する問題」だね。この選択する主体のことを「エージェント」というよ。もうちょっと具体的な例でいうと、このエージェントが将棋をプレイするエージェントなら、毎ステップの「状態」は「自分の手番の直前の盤面」で、「行動」は「どんな手を指すか」だね。このエージェントが先手なら「 $S_0 =$ 初期配置」で「 $A_0 =$ 2六歩」とかかもしれないね。そしたら後手も何か手を打ってくるから、 $S_1$ はそれに応じた盤面になって、それを受けてエージェントは打つべき手 $A_1$ を判断する。その繰り返し。

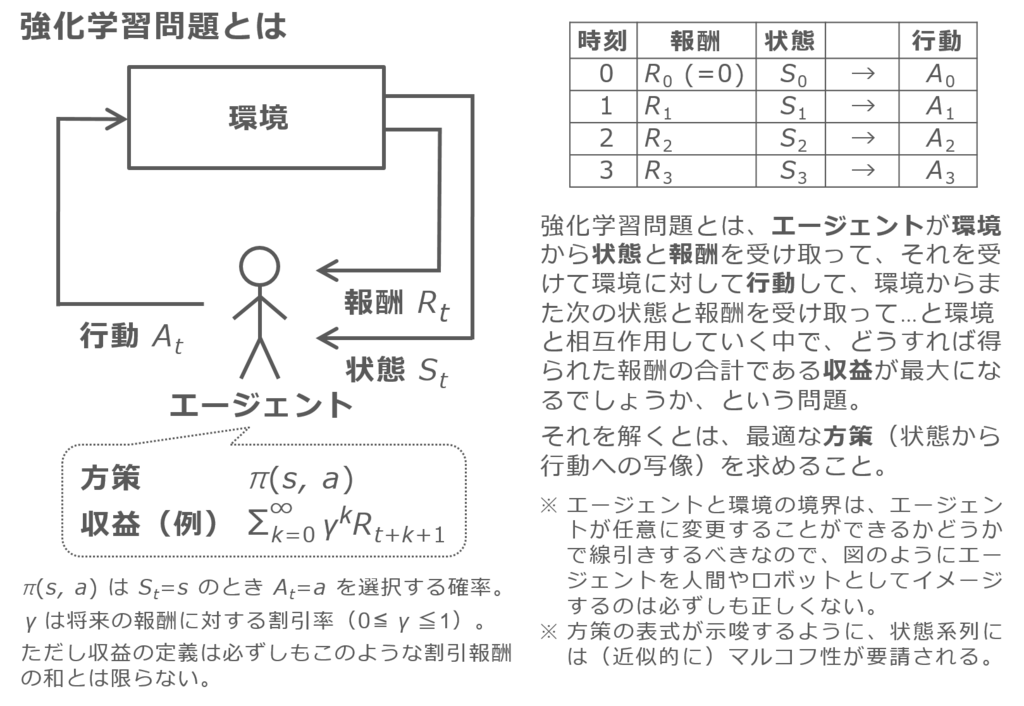
※	絵の右下の方に「マルコフ性が要請される」とありますが、これは、「行動は現在のステップの状態だけで判断できる」＝「現在のステップより過去のステップの状態がどうだったかの情報はつかわない、あっても行動の判断に影響を及ぼさない」という意味です。基礎的な強化学習の話ではよく置かれる仮定と思います。

私がエージェントならば角道を開けたいですね。

いいよ別に角道開けても…。

「状態」とは毎ステップ観測される盤面で、「行動」とはそれに対して毎ステップ打つ手ということなんですよね？では「報酬」とは何ですか？対局料？

ではないかな。というか「報酬」っていっても現実のお金じゃないからね。「報酬」は強化学習のキモになる概念だよ。エージェントは獲得する「報酬」の和が最大になるように行動を選択する。だから、強化学習を利用する我々はエージェントが思い通りのふるまいをするよう「報酬」を適切に設計しなければならない。もしエージェントを将棋の対局で勝たせたいなら、「エージェントがなるべく多くの報酬を得ようと毎ステップ行動選択すること」が「将棋の対局に勝つこと」につながらなければならない。

なるべくそれを得ようとすることが勝つことにつながる…？ああ、「報酬」とは賞金のことだったんですか。

だから現実のお金から離れ…なくてもいいか。その試合に勝った場合のみに賞金がもらえるとかなら、別に賞金でも構わないよ。一般に強化学習の報酬は、状態が遷移する度に毎ステップ得られるものとして定義されるけど、賞金を報酬にするなら、対局が終わったステップであってかつ勝った場合のみに得られる報酬になるね。というか実際ボードゲームをプレイするエージェントではよくそのような報酬が設計されるね。にしてもなんで部長の中でこのエージェントはプロ棋士として生計を立ててるのさ…。

でも、賞金を得ようという心意気やよしですが、どうしたら勝てるのかって対局相手によりませんか？対局相手の得意とする戦型を研究しておく必要があるのではないでしょうか？

…そこまで考慮したかったら「対棋士Aエージェント」「対棋士Bエージェント」というように対局相手ごとに学習すればいいと思うよ。

対局相手によって異なる指し方ができるんですか？いま賞金を「報酬」としただけですよね？

できるよ。盤面に対して打つ手の「価値」が違ってくるからね。全く同じ盤面でも、ある手を打つことが対棋士Aでは自分の優勢につながるが対棋士Bでは自分の劣勢につながるというケースがもしあったら、「なるべく報酬を得よう」とするとき選択する行動は異なってくるよね。ある盤面である手を打ったとき、それ以降にどれだけの報酬が得られるかの期待値を、その盤面と打ち手に対する「価値」というよ。そして通常はより「価値」の高い手を選択する。でも「価値」はわからない。だから推定する。さっき強化学習とは「毎ステップ適切な行動を選択する問題」といったけど、もっと言い換えると「あらゆる状態で取りうる行動を取ったときのそれぞれの価値を推定する問題」といえるね。

なるほど…。

序文の続きには、本書の構成についてかいてあるね。第1版から変更があったのは上でもみた通りだけど、第2版の第I部は、厳密に解ける場合のテーブル形式の解法になってる。

さっきも思ったんですが「テーブル形式」って何です？

第1版の邦訳の87ページに「テーブル形式手法」とあるね。要は各状態とか各状態行動ペアの1つ1つについて価値を推定する解法だね。環境がどのように応答してくれるかがわかっていれば、強化学習問題は原理上はこの方法で厳密に解くことができる。ただし、現実の問題では往々にして状態の数がとてつもない数になる。だから現実にはあまりテーブル形式手法は適用できない。とはいえ、まず基本的な場合にどのように解くのかを抑えるのが物の順序ということだろうね。

xivページ8行目の both learning and planning methods というのは？学習手法と計画手法？計画とは？？

邦訳版の9章がそのまま「プランニングと学習」というタイトルだね。そこをみると、強化学習問題の解法の中でも、環境モデルを明示的に必要とする解法を「プランニング手法」、環境モデルを明示的には必要としない解法を「学習手法」というみたいだね。あ、環境モデルってのは「環境がどのように応答するか」つまり「状態がどのように遷移するか」と「どのような報酬が得られるか」ね。それが明らかにわかっていたら後はどう行動するかを計画するだけって感じだから「プランニング手法」なのかな。わかっていない場合はとりあえず行動してみてその結果に応じて価値を推定していくことになるから、「学習手法」とよぶのかもしれないね。

序文からして強化学習の知識を前提としすぎではありませんかね…続きは私が読みましょう。第I部ではその「学習手法」も「プランニング手法」もどちらも扱いますし、さらにそれらの融合である n-step methods や Dyna も扱うということです。第2版で初出のアルゴリズムも多く、UCB, Expected Sarsa, Double learning, tree-backup, Q(σ), RTDP, MCTS がそうであると。続く第II部では、第I部で身に付けた強化学習問題の考え方を関数近似に拡張していきます。第II部にも新しい内容が追加されていて、ニューラルネットワーク, fourier basis, LSTD, kernel-based methods, Gradient-TD and Emphatic-TD methods, average-reward methods, true online TD(λ), policy-gradient methods がそうです。第2版では特に方策オフ型の学習手法が拡充されているらしいです。また、forward-view と backward-view を別々の章に分離したのも第1版からの変更だと。

邦訳版の7章に「前方観測的な見方」「後方観測的な見方」というトピックがあるけど、なぜ分離したのかは気になるね。

第III部では新章として強化学習と psychology との関係や neuroscience との関係が追加され、AlphaGo と AlphaGo Zero を含む最近のケーススタディも紹介されているということです。これらのケーススタディの選定の軸は、モデルフリーでかつスケーリングするというところにあるみたいですね。そんなこんなで第2版は第1版の2倍のボリュームになってしまったと。序文の残りは割と謝辞ですかね。

（次回があれば）つづく

2018-12-31

パターン認識と機械学習下（第6章：その6〈終〉）

本読み機械学習

以下の本を読みます。上巻を読むこともあります。何か問題点がありましたらご指摘いただけますと幸いです。

パターン認識と機械学習下 (ベイズ理論による統計的予測)

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/02/29
メディア: 単行本
購入: 6人クリック: 14回
この商品を含むブログを見る

前回：その5

f:id:cookie-box:20180305232608p:plain:w60

まだ 6.4.5～6.4.7 節を残していますが、「第6章カーネル法」のここまでの内容についてふり返っておきたいと思うんです。6.1～6.4 節はそれぞれ以下のような内容だったと思います。

線形基底関数モデル $y(x)=w^{\top}\phi(x)$ における正則化項付き二乗和誤差最小化問題は、 $\{w_n\}$ の最適化問題から $\{a_n\} \equiv \{-\lambda^{-1}(w^{\top}\phi(x_n) - t_n)\}$ の最適化問題に読み替えることができる。つまり、特徴 $\phi(x)$ の重みを解くのではなく、カーネル関数 $k(x_n, x)=\phi(x_n)^{\top} \phi(x)$ の重みを解くことができる（6.1節双対表現）。
つまり、このような問題設定下では、線形基底関数モデルの特徴 $\phi(x)$ を設計する代わりに、カーネル関数 $k(x, x')$ を設計することができる（特徴を明示的に扱うことを回避することができる）。もちろんカーネル関数を直接設計する場合は自由な関数を選んでいいということではなく、それがある特徴の内積となっている $\Leftrightarrow$ 入力空間からの任意のサンプルデータセットのグラム行列（各成分が $k(x_n, x_m)$ である行列）が半正定値である必要がある（6.2節カーネル関数の構成）。
回帰モデルの入力変数／重みパラメータ／目標変数が確率的であると考えるとき、未知の点における（平均）解は既知の点の値をその点までの距離に依存する関数（動径基底関数；RBF）で重みづけして足し上げたものになる。特に線形基底関数モデルの重みパラメータ分布をベイズ更新する問題設定では、この重みを与える RBF は「等価カーネル」とよばれる。なお、この等価カーネルは元の特徴の内積ではない。内積が等価カーネルとなるような新しい特徴を選べばその内積にはなっている（6.3節 RBFネットワーク）。
線形基底関数モデルの重みパラメータ分布をベイズ更新する問題設定において、「まだ何も観測していない下での目標変数の分布」を観測した点によって条件付けるという考え方で解くと、その事前分布の分散共分散行列の各成分は $k(x_n, x_m) = \alpha^{-1} \phi(x_n)^{\top} \phi(x_m)$ となる（6.4節ガウス過程）。

f:id:cookie-box:20180305231302p:plain:w60

確かにここまでそんな内容だったな。

ここでハヤトに質問です。つまり、カーネル関数って何ですか？

えっ？

6.1～6.4 節のどの節も、それぞれ「このような関数はカーネル関数である」を主張しています。そのような箇所を抜粋すると以下です。

「ここでは、線形回帰モデルで、パラメータが以下のような正則化された二乗和誤差を最小化することで求められるようなものを考える。（中略）なおここで、(6.1) で定義されるカーネル関数 (kernel function) $k(x, x')$ を使った」（下巻2～3ページ）
「関数 $k(x, x')$ が有効なカーネルであるための必要十分条件は、任意の $\{x_n\}$ に対して、要素が $k(x_n, x_m)$ で与えられるグラム行列 $K$ が半正定値であることである」（下巻5ページ）
「最後に、等価カーネル (3.62) は、通常のカーネル関数が満たすべき重要な性質を満たしていることを注意しておく（→6章）。すなわち、等価カーネルは非線形関数のベクトル $\psi(x)$ の内積で表現できる。 $k(x,z) = \psi(x)^{\top} \psi(z)$ 」（上巻159ページ）
「まずは線形回帰の例に立ち返り、関数 $y(x,w)$ の上での分布を考えることで、予測分布を再導出することにする。（中略）ここで、 $K$ は、 $K_{nm} = k(x_n, x_m) = \alpha^{-1} \phi(x_n)^{\top} \phi(x_m)$ を要素にもつグラム行列であり、 $k(x, x')$ はカーネル関数である」（下巻15～16ページ）

6.1 節と 6.4 節では、「このような状況で現れるこの関数はカーネル関数である」という具体例にみえます。6.2 節は状況はいくぶん曖昧ですが、第6章で唯一「この条件を満たせばカーネル関数である」を数学的に与えています。6.3 節の等価カーネルはカーネル関数扱いなのか判断しにくいんですが、上巻157ページにおいて「カーネル関数」と呼称されています。

うーんその中だと 6.2 節が最も一般的に「カーネル関数とは」を説明してるんじゃない？つまり、カーネル関数ってのは、2つの変数（ベクトル）をとる関数でグラム行列が半正定値になるようなやつなんだろ？

そうですね。ハヤトは、機械学習のカーネル関数とは何か人に尋ねて、そのように回答されたらうれしいですか？

うれしいかどうかっていわれると…だから何？って感じはするな。知りたいのはそういうんじゃないっていうか。それで何ができるかとかのが大事じゃない？

なので、カーネル法について記述されている別の書籍も参照するべきだと思ったんです。すると、以下の「学習システムの理論と実現」という本にちょうどカーネル法に関する章があるのを見つけたのでこれを読むことにしました。あ、プロデューサーさんがこの本を選んだ理由は「たまたま部屋から発掘されたから」だそうです。「そういえばかなり昔に買った」「目次をみたらカーネル法があってラッキー」だそうです。

学習システムの理論と実現

作者: 渡辺澄夫,萩原克幸,赤穂昭太郎,本村陽一,福水健次,岡田真人,青柳美輝
出版社/メーカー: 森北出版株式会社
発売日: 2005/07/25
メディア: 単行本
購入: 2人クリック: 10回
この商品を含むブログ (9件) を見る

買った本の目次くらい確認しとけよ…あともっと本を整理しろよ…。

上の本の「第3章カーネルマシン」の内容を興味があるところだけかいつまんでまとめます。多少話の順番が前後していますし、解釈でかいています。

出力が $y \in \{-1, 1\}$ であるときの線形基底関数モデル $y(x)={\rm sgn}\bigl[f(x) \bigr] = {\rm sgn} \bigl[ w^{\top}\phi(x) \bigr]$ の誤り訂正学習（線形分離可能ならば有限回の学習で収束する）では、 $w=0$ を初期値とすれば解は $\displaystyle w = \sum_{n=1}^{N} a_n \phi(x_n)$ になるので、PRML の正則化項付き二乗和誤差最小化問題のときと同様、特徴 $\phi(x)$ を設計するのではなく、カーネル関数 $k(x_n, x)=\phi(x_n)^{\top} \phi(x)$ を直接設計することもできる。
同じ状況でのマージン最大化も同じ解の形にかける（証明略）ので、この場合もカーネル関数を直接設計することができる。
もちろんカーネル関数に自由な関数を選んでいいということではなく特徴の内積の形になっていなければならないが、カーネル関数が満たすべき条件は Mercer の定理で与えられる。これを満たすカーネル関数を Mercer カーネルという。
入力空間 $X$ に対して Merser カーネルを何か1つ選ぶと、Mercer カーネルの固有関数の線形和でかけるような関数全体の集合に、ある内積を入れて関数のヒルベルト空間 $\mathcal{H}$ をつくることができる。このヒルベルト空間には、任意の $x \in X$ と $f \in \mathcal{H}$ に対して $\langle f, K_x \rangle_\mathcal{H} = f(x)$ となるような $K_x$ が存在することがわかる（というか Mercer カーネルがそれになる）。このような $K_x$ をもつヒルベルト空間を再生核ヒルベルト空間（RKHS）という。だから何なのかというと、RKHS である $\mathcal{H}$ では、学習データ $\{(x_n, y_n)\}_{1 \leqq n \leqq N}$ に対するあるクラスの正則化項付き最小化問題の $\mathcal{H}$ 内での最適解 $f$ が、各学習データの入力変数に対する $K_{x_n}$ の和でかけることが保証されている（レプリゼンタ定理）。

これ以降に、カーネル関数の例やカーネル関数を用いた手法の例が簡単ですが PRML より1つ1つ丁寧にかかれているようです。

えっと、その1点目と2点目はカーネル関数の具体例みたいだけど、PRML と若干違うんだな。PRML から具体例が増えたって感じだ。3点目はカーネル関数が満たすべき条件だけど、それは PRML の 6.2 節にもあったよな。ここで新たにわかったのは、その条件に「Mercer の定理」という名前が付いていたってことか（※）。4点目は長いなー。ヒルベルト空間？って何？？

※

学習システムの～の本で出てくる Mercer の定理（48ページ）は PRML と少し表現が異なりますが、49ページに補足されている通り PRML 5ページで出てくる表現と等価です。ただし、学習システムの～の方には、PRML にはない「 $k$ が対称関数」という条件が追加されています。これは、 $k$ が実カーネルなら必要で、 $k$ が複素カーネルなら不要（半正定値を課すだけでエルミート性をもつため）な条件です。以下のサイトを参考にさせていただきました。
My_NoteBook/情報工学_カーネル法_Note.md at master · Yagami360/My_NoteBook · GitHub

数学的側面についても調べたのでいつかプロデューサーさんにやる気が出たら別途まとめたいですが、4点目の言いたいことは気持ち的にはこうですかね。

あなたは手元に

学習データ $\{(x_n, y_n)\}_{1 \leqq n \leqq N}$ （ $x \in X, \, y \in \mathbb{R}$ ）と、
それをつかって解きたい $y = f(x)$ の最適化問題 $\underset{f}{\rm minimize} \; G\bigl(\{(x_n, y_n, f(x_n) )\}_{1 \leqq n \leqq N} \bigr)$ と、
$X$ における適当に選んだ Mercer カーネル $k(x, x')$

をもっているとします。つまり、あなたはなるべくよい関数 $f$ を探したいわけですが、もしあなたが最小化したい目的関数 $G$ がレプリゼンタ定理（※）の目的関数の形にあてはまっているなら、

$\displaystyle f(x) = \sum_{n=1}^{N} a_n k(x_n, x)$ の $\{a_n\}$ を最適化することが、
$k$ の固有関数 $\psi_m \, (m = 1, 2, \cdots)$ の線形和でかける関数全体 $\mathcal{H}$ の中から最適な $f$ を探すこと

と同じになります。選んだ $k$ によっては $\psi_m$ は可算無限個になりますが、それでもです。なので、このことを利用するととてもとてもたくさんの関数の候補の中から一番よい $f$ を探すことができます。有限個の $\{a_n\}_{1 \leqq n \leqq N}$ を求めるだけでです。

つまり、PRML での「正則化項付き二乗和誤差最小化」も、学習システムの～で出てきた「誤り訂正学習」も「マージン最大化」も、この主張の個別の具体例だったというわけです。

※

レプリゼンタ定理の主張はこうです。 $k$ を Mercer カーネルとし、 $k$ の定める再生核ヒルベルト空間を $\mathcal{H}$ とおくと、正則化問題 $\displaystyle \underset{f \in \mathcal{H}}{\rm minimize} \; G_{\rm emp} \bigl(\{(x_n, y_n, f(x_n) )\}_{1 \leqq n \leqq N} \bigr) + G_{\rm reg} \bigl( \langle f, f \rangle_{\mathcal{H}} \bigr)$ の解 $f \in \mathcal{H}$ はサンプル点におけるカーネル関数の重み付き和 $\displaystyle f(x) = \sum_{n=1}^{N} a_n k(x_n, x)$ で表されます。ここで $G_{\rm emp}$ は実数値関数で、 $G_{\rm reg}: \mathbb{R} \to [0, \infty)$ は狭義単調増加関数です（学習システムの～ 61ページ参照）（この本に証明はないです）（より一般的な表現もありえます）。

※

ついでに Mercer カーネル $k$ が定める再生核ヒルベルト空間だけかくと、 $k$ の固有展開を $\displaystyle k(x, x') = \sum_{m=1}^{\infty} \gamma_m \psi_m(x) \psi_m(x')$ としたときに、 $\{ \psi_m \}$ の線形和でかける関数全体の集合 $\mathcal{H}$ であって、 $\displaystyle f(x) = \sum_{m=1}^{\infty} c_m \psi_m(x)$ $, \;$ $\displaystyle g(x) = \sum_{m=1}^{\infty} d_m \psi_m(x) \in \mathcal{H}$ に対して $\displaystyle \langle f, g \rangle_{\mathcal{H}} \equiv \sum_{m=1}^{\infty} \frac{c_m d_m}{\gamma_m}$ という内積を定義した空間です（学習システムの～ 59ページ参照）（ただしこの本の 59～60 ページの説明では無限和になっていないですが、おそらく特徴空間が何次元かを意識してこうかいているのであって、無限和でも成り立つ話のはずですたぶん）。

これまで出てきた具体例を一般的にかくとこうなるってこと？

「カーネル関数で何ができるか」ですよ。僕たちは PRML の 6.1 節で、正則化項付き二乗和誤差最小化の双対問題で、初めてカーネル関数に出会いました。正則化項付き二乗和誤差最小化がカーネル関数によっても解けることは明確でしたが、反面、あまりそのありがたさもわからなかったんです。わざわざ双対問題にする必要があったのかと思ってしまいましたし、よくわからない高次元空間で解を探すよりも特徴を明示的に設計した方がよいような気がしてしまったので。続く 6.2 節ではカーネル関数に主役が移り、さまざまなカーネル関数の例が提示されましたが、ここで出てきた疑問は「どのような問題ならばこれらのカーネル関数をつかうことができるのか」です。カーネル関数をつかえる（※）のは 6.1 節のように最適解が「サンプル点におけるカーネル関数の重み付き和」でかけるような問題に限られます（※ 無限個のパラメータをつかってもよいなら最適解が 6.1 節の形になっていなくてもよいですが、それは全くありがたくないので）。ただ、6章の続きを読んでも、このようにかける問題の全体像がわからなかったんです。

既に答えを知っているのにわざわざ双対問題にする必要があるのかってのもそうだけど、全体的に「カーネル関数はあなたがすでに知っている問題にも現れるんですよ」って説明の仕方だからなんか目新しくなくてつまんないなって思ったんだよな。でも、PRML では一般的な議論を避けて個別事例の双対性を示していくスタンスだったからそうならざるをえなかったんだな…。

逆に「学習システムの理論と実現」にあるレプリゼンタ定理から出発するともう少しわかりやすかったんです。「再生核ヒルベルト空間」という特定の性質をもつ関数空間から関数を探すならば、「サンプル点に対応する再生核（＝カーネル関数）がつくる部分空間」の中に目的関数を最小にする関数があるんです。これは本来可算無限個の重みを求めなければならなかったところが有限個の重みを求めるので済むので、とてもお得です。だから再生核ヒルベルト空間がほしいんです。それは再生核となる Mercer カーネルを与えれば定まります。だから Mercer カーネルがほしいんです。僕たちが Mercer カーネルを選ぶのは「それなら内積の形でかけるから」とか「個別データの特徴よりもデータ間の類似度の方が設計しやすいから」とかではないんです（※ とかでも正しいです）。「再生核がほしいから」なんです。Mercer カーネルを1つ選んだとき、そこに再生核ヒルベルト空間が広がるんです。

ごめんよくわかんない。

ちなみに Mercer の定理やレプリゼンタ定理の証明までしたかったら学習システムの～の本にもそこまでは触れていないので、真面目に関数解析の勉強をしてください。また、カーネル法の入力は文字列や記号でもよいということですが、入力空間が満たすべき（＝カーネル関数が級数展開できる）条件を知るには、より一般の測度空間を扱うための知識も必要です。

無理無理無理。

PRML の 6 章の残りですが、軽く流しましょう。6.4.5 節ですが、ガウス過程回帰を分類につかいたいということですね。出力が $\{0,1\}$ の2値分類ならば、モデルの出力にロジスティックシグモイド関数を適用すればどちらのラベルであるかの確率に変換できます。変換する前の出力に対する事前分布はガウス過程回帰のときと同じです。学習データ点が $N$ 点手に入ったときの未知の点に対する予測は (6.76) 式なんですね。解析的に解けないらしいです。

解けないのかよ！なんか解けるように上手くやってるのかと思ったのに！

ロジスティックシグモイド関数とガウス分布の重畳積分の近似公式が上巻の (4.153) 式にあって、これを利用して事後分布をガウス分布で近似するらしいですね。しかも解き方は3つあって、変分推論法、EP法、ラプラス近似ということです。分類問題をベイズ的に解くのはどれが定番というのはないのでしょうかね。多クラス分類にも対応できるかとか、計算量の違いとか特色があるんでしょうか。6.4.6 節ではこの内ラプラス近似がピックアップされていますね。…とばしていいですかこの節？

Mercer の定理やレプリゼンタ定理で力尽きてるだろこれ…。

最後の 6.4.7 節が「ニューラルネットワークとの関係」ということなんですが、この節はあくまで「ガウス過程とニューラルネットとの関係」であって「カーネル法とニューラルネットとの関係」という話ではないですね。内容としては、

ニューラルネットワークも、ベイズ的に重みの分布を更新することができる。
ニューラルネットの生成する関数がしたがう分布は、隠れ層のニューロン数を無限に増やした極限では 6.4.1, 6.4.2 節同様にガウス過程に近づくことが示されているが、この極限では出力ベクトルの成分間が独立になってしまうことに注意。
特定の活性化関数を用いた場合のガウス過程の分散共分散行列は導かれているが、この場合のカーネル関数はもはや差 $x-x'$ の関数とはならないことに注意。
重みの事前分布を超パラメータで調整することも考えられる。超パラメータは「どのようなスケールの出力を出すか」「どのような範囲の入力に反応するか」を左右する。6.4.3 節では、共分散が超パラメータの関数であるときに超パラメータを最尤推定する手法を扱ったが、このときと同様、ニューラルネットの重みの事前分布を支配するパラメータも解析的に厳密に最適化はできないことに注意。

ニューラルネットも重みをベイズ更新すればガウス過程ととらえられるのか。で後ろ3点は、全部注意かよ。

本には注意とはかいてませんけどね。

…2段落目の最後の方の「『統計的な強度を借りる』」って何？カギカッコ付いてるから、正式な用語じゃなくて比喩的なフレーズなんだろうけど、意味わかんなくない？

原著をあたった方がわかりやすいかと思ってみてみたんですが、そのまま ‘borrow statistical strength’ だったんですよね。

何の解決にもなってないな。

でも、例えばニューラルネットの出力が身長と体重の2変数だったとして、身長を算出するために1つ手前の層の出力にかける重みが学習データ中の身長からのみ影響を受けるかというとそうではなくて体重からも間接的に影響を受けるはずですよね。…そんなニューラルネットの学習があるのかどうか知りませんが…。

そういえばジュンさっきこの節はあくまで「ガウス過程とニューラルネットとの関係」であって「カーネル法とニューラルネットとの関係」という話ではないっていってたけど、じゃあカーネル法とニューラルネットは何か関係あるの？

パーセプトロンの学習がレプリゼンタ定理にあてはまるクラス（解がサンプル点におけるカーネル関数の重み付き和でかける）であることは6章の演習問題 6.2 にそれを示せという問題があるんです。これの示し方は誤り訂正学習のときと同じです。 $w$ の初期値をゼロベクトルにすれば $w = \sum_{n=1}^{N} \eta t_n \phi(x_n)$ になります。ただニューラルネットとの関係というには多層パーセプトロンとの関係が知りたいですよね。PRML の中でその話が出てくるかは見つけていませんが、最近発売された以下の雑誌にカーネル法とニューラルネットワークとの関係の話があるらしいです。

数学セミナー2018年12月号｜日本評論社

（次章も読むなら）つづく

2018-12-17

パターン認識と機械学習下（第6章：その5）

本読み機械学習

以下の本を読みます。上巻を読むこともあります。何か問題点がありましたらご指摘いただけますと幸いです。

パターン認識と機械学習下 (ベイズ理論による統計的予測)

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/02/29
メディア: 単行本
購入: 6人クリック: 14回
この商品を含むブログを見る

前回：その4 ／次回：まだ

前回 6.4.1 節のあらすじです。

f:id:cookie-box:20181209153534p:plain:w720

ガウスカーネルの場合と指数カーネルの場合で2列にまとめてみたんですが、内容がほぼ一緒なのであまり2列に分けた意味ありませんでしたね。

まだ事前分布じゃん！あと本当に2列に分けた意味ないな！

早く事後分布に更新しましょう。…の前に、前回はガウスカーネル及び指数カーネルを考えていましたが、6.4.2 節では (6.63) 式の形式のものが広くつかわれているとありますね。(6.63) 式のパラメータを色々な値に変えてプロットしたものが図 6.5 だと。

(6.63) 式は、 $\theta_2 = \theta_3 = 0$ ならガウスカーネルだな。図6.5 の一番左上がそうだ。図 6.5 の上段真ん中は形だけはその左と同じで、縦方向に $\sqrt{\theta_0}$ 倍に拡大されているだけだな。上段一番右は… $\theta_1$ が16倍になってて、つまり、「ガウスカーネルの分散」が16分の1になっているから、「近い点どうしは相関が強いはず」の「近い点」の範囲が4分の1に狭くなっているんだな。だから左側2枚より波打ってる。逆に左下は「近い点」の範囲が4倍になってなだらかになってるな。残り2つは…？

下段真ん中は一番左上の図の分散共分散行列のすべての成分に定数 $\theta_2=10$ が加わっています。「近い点どうしは相関は強いはず」に加えて、「全ての点どうしはある程度相関が強いはず」というのが加わった感じですね。なのでサンプルされた点列はプラス側だったら全体的にプラス側、マイナス側だったら全体的にマイナス側に出ていますよね。一番右下は線形項がある場合ですね。1次元の内積なのでただの積ですが…この図の左端と右端の点どうしが一番負の方に相関が強くなるはずですね。なので実際描かれているグラフも両端で符号が逆側になっているのが多いです。ゼロ付近では線形項の効果はあまりなく、両端に行くほど近い点どうしの相関が強くなっていくはずです。定数項と線形項は、(6.63) 式の下にかいてあるように考えている線形基底関数モデルが通常の線形モデルと同じ項をもつようにするためにあるような気がしますけど。

事前分布はもう飽きてきたな。この図 6.5 をどうやって事後分布に更新するの？

6.4.2 節では、仮定として $y_n \equiv w^{\top}\phi(x_n)$ は直接観測できず、観測可能なのは $y_n$ にガウス分布にしたがうノイズ $\varepsilon_n$ が加わった目標変数 $t_n$ のようですね。 $t_{1:N}$ の事前分布を求めるには (6.61) 式の積分をすればよく、分散共分散行列の各要素は (6.62) 式になりますね。そして、いま求めたいのは $p(t_{N+1}|t_{1:N})$ です。 $N$ 個の観測値を得たときの、次のまだ見ぬ観測値 $t_{N+1}$ に対する分布です。…が、6.4.2 節を最後まで見る限り、どうも $w$ が更新されている式はありませんね。

は？じゃあ $w$ の分布は (6.50) 式の事前分布 $p(w) = N(0, \, \alpha^{-1}I)$ のままってこと？ $N$ 個の観測値が得られたのに重みは更新されないってどういうことだよ？それじゃ $y_{1:N}$ の分布ごちゃごちゃしたままじゃん（下図）。回帰モデルだったら重みを求めるだろ普通。

f:id:cookie-box:20181205233338p:plain:w240

あ、いえ、 $w$ 自体を更新してはいないというだけです。 $w$ は間接的に更新されています。何も観測していない下での目標変数の同時分布 $p(t_{1:N+1})$ を既に観測した $t_{1:N}$ で条件付ける形で（式 6.66, 6.67）。しかし、更新後の $w$ の分布は直接あらわれていません。ここから $w$ の分布を逆算することはできるかもしれませんが、する意味もありません。いま興味があるのは $t_{N+1}$ の分布であって、 $w$ の分布には正直興味がないんです。

そこまでいうとなんか $w$ がかわいそう！

未知の点 $x_{N+1}$ に対応する目標変数の予測分布の平均と分散は以下ですね。

$m(x_{N+1})=\bigl( \begin{array}{ccc} k(x_1,x_{N+1}) & \cdots & k(x_N,x_{N+1}) \end{array} \bigr) \left( \begin{array}{cccc} k(x_1,x_1) + \beta^{-1} &k (x_1,x_2) & \cdots & k(x_1,x_N) \\ k(x_2, x_1) & k(x_2,x_2)+\beta^{-1} & \cdots & k(x_2, x_N) \\ \vdots & \vdots & & \vdots \\ k(x_N, x_1) & k(x_N, x_2) & \cdots & k(x_N, x_N) +\beta^{-1}\end{array} \right)^{-1} \left( \begin{array}{c} t_1 \\ \vdots \\ t_N \end{array} \right)$
$\sigma^2(x_{N+1})=k(x_{N+1},x_{N+1})+\beta^{-1}$
$\quad -\bigl( \begin{array}{ccc} k(x_1,x_{N+1}) & \cdots & k(x_N,x_{N+1}) \end{array} \bigr) \left( \begin{array}{cccc} k(x_1,x_1) + \beta^{-1} &k (x_1,x_2) & \cdots & k(x_1,x_N) \\ k(x_2, x_1) & k(x_2,x_2)+\beta^{-1} & \cdots & k(x_2, x_N) \\ \vdots & \vdots & & \vdots \\ k(x_N, x_1) & k(x_N, x_2) & \cdots & k(x_N, x_N) +\beta^{-1}\end{array} \right)^{-1} \left( \begin{array}{c} k(x_1,x_{N+1}) \\ \vdots \\ k(x_N,x_{N+1}) \end{array} \right)$

もし観測値が1つしか得られていない状況で未知の点の値を予測すると $\displaystyle m(x_{N+1})=\frac{k(x_1,x_{N+1})}{k(x_1,x_1)+\beta^{-1}}t_1$ なので、これは既知の観測値をその観測値への事前分散で割って、未知の点からみてその点との間の共分散をかけた値になっていますね。また、 $\displaystyle \sigma^2(x_{N+1})=k(x_{N+1},x_{N+1})+\beta^{-1} -\frac{k(x_1,x_{N+1})^2}{k(x_1,x_1)+\beta^{-1}}$ で、この最後の項を除くと「何も知らない下での $x_{N+1}$ における目標変数の分散」になっているので、最後の項は既に観測値を1つ知っているために分散が小さくなったという効果になりますね。既に値が観測されている点との間のカーネル関数が大きい（既に値が観測されている点に近い）点では分散が小さくなりますが、そうでない点では分散が大きいままになります。それが図 6.8 に示されていますね。この図 6.8 は、x軸のそれぞれの点で $m(x)$ と $\sigma^2(x)$ を計算してプロットしたものだと思います。どの既知の点からも遠い図の右側の方がグレーの帯が太くなっています。なんだか未知の点における予測分布が既知の観測値に支配されている感じがしないでしょうか？

うーん、まあ何となくは？あれでもさ、観測値を得る前ってなんか糸くずみたいにごちゃごちゃしてなかった？上の絵みたいに。こんな帯みたいな感じじゃなくなかった？

糸くずみたいな絵、つまり、さまざまな $x$ において同時に取る値のありうるシナリオの1つを描くこともできるはずです。例えば未知の $M$ 個の点に対して $t_{N+M}$ の同時分布の共分散行列の分割を行えば $t_{N+1:M}$ の平均ベクトルと共分散行列が得られます。それさえあればその糸くずみたいな絵を描いたのと同じ要領で $M-N$ 変量正規分布から点をどんどんサンプリングすればいいだけです。もっとも、今度の糸くずみたいな絵は既に手に入っている $N$ 個の観測値に寄り添ってまとまってくると思います。計算するの面倒そうですし、それを描いてもさほどありがたくなさそうですが。

でも15ページで散々「関数に対する事前分布」「関数 $(y,w)$ 上での分布」って言って、その事前分布としてガウス過程を導いたんだから、事後分布も関数の分布であってほしくない？このグレーの帯じゃ関数の分布じゃなくて各点での値の分布じゃん。

まあそれはそうですね。

なんか一貫してない気がするんだよな。まあいいけど…あ、そういえばこの21ページの「 $k(x,x')$ が有限の基底関数で定義される場合には、3.3.2 節で得られた、ガウス過程の観点から導いた線形回帰の結果を再び導くことができる」って何だろ。上巻を見なきゃか…あ、今日上巻もってないや。というか下巻だけでも持ち歩くの十分重いんだよな…。

それならもう持ち歩く必要はありませんよ。PRML は先月無料で公開されましたから。

Christopher Bishop at Microsoft Research

英語じゃん！まあ背に腹は代えられないから読むけど…ってあれ？この 3.1 節の数式いまの状況と同じ…てかこの (3.55) 式、こっちではちゃんと尤度最大化で $w$ 求めてるじゃん！ $w$ かわいそうじゃない！あ、しかも Figure 3.9 には糸くずみたいな事後分布も載ってる！

なるほど。6.4.2 節ではそもそも $w$ を求める必要がありませんでしたが、 $w$ に興味があったとしても基底関数が無限にあったら無限次元の $w$ の事後分布をとらえることはできませんでしたね。でも基底関数が有限個なら Figure 3.7 のように $w$ をベイズ更新することができて、 $w$ の分布からのサンプリングで Figure 3.9 を描くことも容易（ $w$ の分布さえあれば）ですね。

基底関数が有限個だったらパラメータ空間で解く解き方も、ガウス過程を考える解き方も、どっちの解き方もできるのか。どっちが楽なんだろ。この Figure 3.7 って前の時刻の分布に尤度かけていっているだけだよな。だったらパラメータ空間で解くのって楽そう？一方で 6.4.2 節のガウス過程は…「最も大きな計算量を要する部分が、 $N \times N$ の行列の逆行列を計算する部分であり」？確かにさっきジュンがかいた式何気に逆行列取ってるじゃん。計算量つらそう…。

まあそれで無限の特徴を扱えるようになったと思えば…訓練データが大きい場合のための近似手法もあるようですね。

6.4.3 節は、超パラメータの学習？ここでの超パラメータって何？

おそらく観測ノイズの精度 $\beta$ と、(6.63) 式の $\theta_0, \theta_1, \theta_2, \theta_3$ などではないでしょうか。

それらを尤度最大化で推定することもできるってことか。それで、6.4.4 節は、その応用（？）みたいな感じで、各訓練データ点からの寄与度を推定することで、役に立たないゴミみたいなデータを除けるって話だな。

（次回があれば）つづく

2018-12-14

雑記： Schur 補行列と Sherman-Morrison-Woodbury の公式とカルマンフィルタとガウス過程回帰の整理

雑記

公式の証明はありません（参考文献の1つ目に詳しいのでそちらをご参照ください）。何か問題点がありましたらご指摘いただけますと幸いです。

参考文献

（2018-12-15 追記）先にこの記事は何なのかというと、カルマンフィルタとガウス過程回帰は、どちらも観測にノイズがのっていたり何かを予測したかったり解くときにブロック行列に関する公式が出てきてちょっと似ている気がすると思います。何を知りたくて、その知りたいものは何にしばられているのかをまとめるとこうなると思います。

	カルマンフィルタ（のフィルタ操作）	ガウス過程回帰
知りたいこと	直接観測できない「状態」が、いまどう分布しているか知りたい。 $p(x_t\|y_{1:t})$	空間内の「目標変数」が、それをまだ観測していないある点でどう分布しているか知りたい。 $p(t_{N+1}\|t_{1:N})$
知っていること	いまの観測を知らない下で予測されるいまの状態の分布は知っている。 $p(x_t\|y_{1:t-1})$ 状態がわかっている下で得られる観測の分布は知っている。 $p(y_t\|x_t)$ いまの観測は知っている。 $y_t$	何も知らない下で空間内のいくつかの目標変数がどう分布するかは知っている。 $p(t_{1:N+1})$ いくつかの点での目標変数は知っている（訓練データ）。 $t_{1:N}$
やること	$p(x_t\|y_t) \propto p(y_t\|x_t)p(x_t\|y_{1:t-1})$ を計算する（多変量正規分布の積の平方完成）。 → Sherman-Morrison-Woodbury 公式を使用。	$p(t_{1:N+1})$ を $t_{N+1}$ のみの関数にする（多変量正規分布で一部変数を固定する形の平方完成）。 → Schur 補行列を使用。
補足	結局いまの状態の分布は、いまの観測を知らない下でその状態である確率と、その状態からいまの観測が得られる確率の積に比例する。	未知の点における目標変数の分布は、すでに知っている点とのカーネル関数にしばられている（目標変数 $t_n$ は $t_n = y(x_n) + \varepsilon_n$ であり、 $y(x_n) = w^{\top}\phi(x_n)$ であり、 $p(w)=N(0, \alpha^{-1}I)$ という仮定をおいている。そのため、何も知らない下で、 $y(x_1), \cdots, y(x_N)$ は行列の各成分が $\alpha^{-1}\phi(x_n)^{\top}\phi(x_m) =\alpha^{-1}k(x_n, x_m)$ となる共分散行列をもつ多変量正規分布にしたがう）。
互いに相手っぽく解くには	$p(x_t, \, y_t\|y_{1:t-1})$ を $x_t$ のみの関数にする（同時分布を出すのは面倒。もっとも、普通に解くのも面倒）。	$p(t_{N+1}\|t_{1:N}) \propto p(t_{1:N}\|t_{N+1})p(t_{N+1})$ を計算する（原理上はこうだがやっていないからわからない。というか $p(1:N\|t_{N+1})$ は結局 $p(t_{1:N+1})$ において $t_{N+1}$ を固定することになりそうなので、最初から $t_{1:N}$ の方を固定しろという話にはなる）。
結論	素直に解いた方がいいと思います。

上の表に一部かいてしまいましたが、先にタイトルを回収すると以下です。

Schur 補行列とは、「ある行列に対して、その行列の逆行列の左上（または右下）のブロックをとって、その逆行列を取ったもの」。「ある行列に対して、その行列の逆行列の左上（または右下）のブロックをとって、その逆行列を取ったものがほしい」というときにつかう。どういうときにそうなるかというと、「多変量正規分布にしたがう確率ベクトルのうち一部の変数たちを固定して、その条件下で残りの変数たちがしたがう多変量正規分布の分散共分散行列を知りたい」というとき。
Sherman-Morrison-Woodbury の公式とは、適当なサイズの4つの行列に対して成り立つ恒等式であって、どんなときに役立つかというと、行列の逐次更新式の形が「時刻 $t-1$ の行列の逆行列に他の行列を足してから逆行列をとったもの」のようになっているときに、この公式で書き換えた方が計算量的に有利になることがある（逆行列側で更新しろという形だが、諸事情で逆行列側だけでは手順が進められないとき）。別に Sherman-Morrison-Woodbury の公式がないと死ぬわけではない。ただ計算量というのは馬鹿にできないので、やっぱりないと死ぬかもしれない。Schur 補行列との関係は、この公式自体が Schur 補行列による逆行列のブロック表示からきれいに導かれるのと、だから逐次更新したい行列が Schur 補行列の逆行列型になっていたらこの恒等式で書き換えできる。書き換えるとやはり Schur 補行列の形をしている。
カルマンフィルタでは、状態ベクトルの分布を、時刻ごとに得られる観測ベクトルにしたがって更新していくが、このうちフィルタ操作（一期先予測分布からフィルタ分布への更新）では、フィルタ後分散共分散行列が Schur 補行列の逆行列型になる。なので、Sherman-Morrison-Woodbury の公式で書き換えて計算量を減らすことが多い（状態ベクトルの次元数よりも、観測ベクトルの次元数の方が小さいときにはこれが有効で、実際カルマンフィルタの適用場面ではそのようなシチュエーションが多い）。フィルタ操作に Schur 補行列をつかうわけではない。

ただし、カルマンフィルタにおいて、状態ベクトルと観測ベクトルを連結したベクトルを考えれば、フィルタ操作を「多変量正規分布を一部の変数で条件付けたい」ととらえることはできる。このようにとらえるなら、フィルタ操作に Schur 補行列をつかうことになる。あまりこうとらえないとは思う。このやり方で解くとフィルタ後分散共分散行列が直接 Schur 補行列型になる（つまり、逆行列の形で出てくるのではなく、直接 Sherman-Morrison-Woodbury の公式で書き換えた後の形が出てくる）。

普通（？）にベイズ更新式からカルマンフィルタを解く場合はフィルタ後分散共分散行列は否応なく逆行列型で出てきてしまう。雰囲気としては、観測モデルの式は状態がわかっている下での観測の分布なので、状態と観測の連結ベクトルの一期先予測分散共分散行列を $D$ に関する Schur 補行列ではなく $A$ に関する Schur 補行列でブロック分割したものになっている。なので、観測モデルから出発した素直な式変形では逆行列型が出てきてしまう。

ガウス過程回帰（PRML下巻 6.4.2 節の）では、目標変数 $t_1, \cdots, t_N$ が観測された下で $t_{N+1}$ のしたがう分布を知りたいが、これは $t_1, \cdots, t_N, t_{N+1}$ のしたがう事前分布のうち $t_1, \cdots, t_N$ を固定することで達成される。つまり Schur 補行列をつかう。

逆にこれをカルマンフィルタ的にとらえると、 $t_{N+1}$ が状態変数で、 $t_1, \cdots, t_N$ が観測変数であり、その間の共分散がカーネル関数でしばられている。状態の方が1次元で小さいので Sherman-Morrison-Woodbury の公式をつかう必要はないし、というか両辺スカラーになる。

ここからメモ（ガウス過程回帰の話はない）です。

以下のサイズの行列 $A, \, B, \, C, \, D$ があるとき、

$A \in \mathbb{R}^{n \times n}, \quad B \in \mathbb{R}^{n \times m}$
$C \in \mathbb{R}^{m \times n}, \quad D \in \mathbb{R}^{m \times m}$ 以下の恒等式で逆行列がとられている行列に逆行列が存在するならば、以下の恒等式が成り立ちます。 $(A + BDC)^{-1} = A^{-1}-A^{-1}B(D^{-1}+CA^{-1}B)^{-1}CA^{-1}$ これを Sherman-Morrison-Woodbury の公式といいます。

え？あ、うん。「そっか、成り立つんだ」って感じなんだけど。なんかうれしいのそれ？あと公式の名前なっが！

$A + BDC$ の逆行列が知りたいときに有用です。右辺 $A^{-1}-A^{-1}B(D^{-1}+CA^{-1}B)^{-1}CA^{-1}$ の方を求めればよいということなので。

ごめん、いうほど「 $A + BDC$ の逆行列が知りたいなー」ってなる？なったとして「右辺の方を求めればいいんだよかったー」ってなる？

例えばカルマンフィルタの問題設定（システム・観測は線形、システムノイズ・観測ノイズ・状態の事前分布はガウシアン）の下では、時刻 $t$ におけるフィルタ分布はベイズの定理より以下のようにかけます（各文字の意味は別の記事を参照してください）。

$\begin{split} p(x_{t} \, | \, y_{1:t}) &\propto p(y_t | x_t) p(x_t | y_{1:t-1}) \\ & = \exp \left( -\frac{1}{2} (y_t - H_t x_t)^{\top} {R_t}^{-1} (y_t - H_t x_t) \right) \exp \left( -\frac{1}{2} (x_t - \mu_{t|t-1} )^{\top} {V_{t|t-1}}^{-1} (x_t - \mu_{t|t-1} ) \right) \\ & = \exp \left( -\frac{1}{2} (y_t - H_t x_t)^{\top} {R_t}^{-1} (y_t - H_t x_t) -\frac{1}{2} (x_t - \mu_{t|t-1} )^{\top} {V_{t|t-1}}^{-1} (x_t - \mu_{t|t-1} ) \right) \\ & \equiv \exp \left( -\frac{1}{2}z \right) \end{split}$

ここで $z$ とおいた部分の、 $x_t$ に依存する項（ $x_t$ のしたがう分布を知りたいので）は以下のようになります。

$\begin{split} z &\propto - {y_t}^{\top} {R_t}^{-1} H_t x_t - {(H_t x_t)}^{\top} {R_t}^{-1} y_t + {(H_t x_t)}^{\top} {R_t}^{-1} H_t x_t \\ & \quad + {x_t}^{\top} {V_{t|t-1}}^{-1} x_t - {x_t}^{\top} {V_{t|t-1}}^{-1} \mu_{t|t-1} - {\mu_{t|t-1}}^{\top} {V_{t|t-1}}^{-1} x_t \\ &= {x_t}^{\top} ({V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t) x_t \\ & \quad - {x_t}^{\top} ({H_t}^{\top} {R_t}^{-1} y_t + {V_{t|t-1}}^{-1} \mu_{t|t-1}) - ({y_t}^{\top} {R_t}^{-1} H_t - {\mu_{t|t-1}}^{\top} {V_{t|t-1}}^{-1}) x_t \\&\equiv {x_t}^{\top} ({V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t) x_t - {x_t}^{\top} \alpha - \alpha^{\top} x_t \end{split}$

これは $x_t$ の二次形式になので、フィルタ分布もガウシアンであり、2次の項 ${x_t}^{\top} ({V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t) x_t$ にあらわれる ${V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t$ こそが求めたいフィルタ後分散共分散行列 $V_{t|t}$ の逆行列に他なりません。上式は $(x_t - \mu_{t|t})^{\top} {V_{t|t}}^{-1} (x_t - \mu_{t|t})$ の形に平方完成できますから（係数比較より $\mu_{t|t} = V_{t|t} \alpha$ となります。 $x_t$ に依存しない定数項の足し引きは $x_t$ の分布の形を変えません）。「 ${V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t$ の逆行列が知りたい（それが求めたい分散共分散行列 $V_{t|t}$ だから）」となったわけです。そしてそれは Sherman-Morrison-Woodbury の公式より $V_{t|t} = V_{t|t-1} - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1}$ です。これより、以下の有名なカルマンフィルタのフィルタ分布（の分散共分散行列と平均ベクトル）が導かれます。

$\begin{split} V_{t|t} &= V_{t|t-1} - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1} \\ \mu_{t|t} &= V_{t|t}\alpha \\ &= \bigl( V_{t|t-1} - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1} \bigr) ({H_t}^{\top} {R_t}^{-1} y_t + {V_{t|t-1}}^{-1} \mu_{t|t-1}) \\&= V_{t|t-1} {H_t}^{\top} {R_t}^{-1} y_t + \mu_{t|t-1} \\&\quad - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1} {H_t}^{\top} {R_t}^{-1} y_t \\&\quad - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1} {V_{t|t-1}}^{-1} \mu_{t|t-1} \\&= V_{t|t-1} {H_t}^{\top} {R_t}^{-1} y_t + \mu_{t|t-1} \\&\quad - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} (H_t V_{t|t-1} {H_t}^{\top} + R_t ){R_t}^{-1} y_t \\&\quad + V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} R_t {R_t}^{-1} y_t \\&\quad - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t \mu_{t|t-1} \\&= V_{t|t-1} {H_t}^{\top} {R_t}^{-1} y_t + \mu_{t|t-1} - V_{t|t-1} {H_t}^{\top}{R_t}^{-1} y_t \\&\quad + V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} (y_t - H_t \mu_{t|t-1}) \\&= \mu_{t|t-1} + V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} (y_t - H_t \mu_{t|t-1})\end{split}$

これらは $K_t \equiv V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1}$ とおくともう少しすっきりかけますね。

$\begin{split} V_{t|t} &= V_{t|t-1} - K_t H_t V_{t|t-1} \\ \mu_{t|t} &= \mu_{t|t-1} + K_t (y_t - H_t \mu_{t|t-1})\end{split}$

何も逆行列補題を適用せずとも分散共分散行列と平均ベクトルを逐次式としてかくことはできます。ただ、逆行列補題を適用しない場合、毎回のフィルタリングで $V_{t|t} = ({V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t)^{-1}$ という逆行列を求めなければなりません。この行列は縦幅も横幅も状態変数の次元数ですが、状態の次元が大きいと大きな行列になりえます。他方、逆行列補題を適用すると $V_{t|t} = V_{t|t-1} - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1}$ で、このインバースの中に入っている行列のサイズは縦幅も横幅も観測変数の次元数です（カルマンフィルタの状況では $A = V_{t|t-1}^{-1}$ の逆行列が既に求まっているので逆行列を求める必要があるのはこのインバースの中身だけになるわけです）。一般にカルマンフィルタの適用場面では「状態変数の次元数 >> 観測変数の次元数」となることが多いので逆行列補題を適用した方が計算コストが小さくなるんです。状態変数の分散共分散を更新したいだけであれば分散共分散行列の逆行列（精度行列）の方を更新していけば逆行列をとる操作を回避することができそうですが、平均ベクトルの更新では平方完成をするために「精度行列の逆行列」が出てきてしまうので。

なっが！えっと、要するに、 $A$ の逆行列がわかっていて、 $A$ と $D$ のサイズを比べると $A$ の方が結構大きいときには $A + BDC$ の逆行列を直接求めるよりも $A^{-1}-A^{-1}B(D^{-1}+CA^{-1}B)^{-1}CA^{-1}$ を求めた方が楽ってこと？それでそういうシチュエーションになる例がカルマンフィルタ？なんか使用場面が限定的じゃない？

適用できる問題が特別だからといって公式の有用性が損なわれるということはないと思いますが。もっとも、この「カルマンフィルタの場合」をもっと抽象化してとらえることができます。逆行列補題に出てくる行列 $A, \, B, \, C, \, D$ は $\left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$ の形に配置すると大きな行列になることに気付きましたか？

え？あー確かに、全体で $(n+m) \times (n+m)$ の大きさの行列になるな。それが？

カルマンフィルタの問題設定で、時刻 $t-1$ までの観測 $y_{1:t-1}$ を得た下での $\left( \begin{array}{c} x_t \\ y_t \end{array} \right)$ なるベクトルのしたがう分布を考えてみてください。 $x_t$ は多変量正規分布にしたがうとしていいです。であれば、 $y_t$ は $x_t$ の線形変換にガウシアンノイズを足したものなのでやはり多変量正規分布にしたがいます。この $x_t$ と $y_t$ を縦に連結した $\left( \begin{array}{c} x_t \\ y_t = H_t x_t + w_t \end{array} \right)$ もプロデューサーさんが何かを勘違いしていなければ多変量正規分布にしたがいます。証明は確率ベクトル $\left( \begin{array}{c} x_t \\ y_t \end{array} \right)$ のモーメント母関数 $\displaystyle E \left[ e^{ \left( \begin{array}{cc} t_1^{\top} & t_2^{\top} \end{array} \right) \left( \begin{array}{c} x_t \\ y_t \end{array} \right)} \right]$ が多変量正規分布にしたがう確率ベクトルのそれと一致することによりました。あ、証明をここにかくのはもう本当に面倒なので省略します。

もう数式打つの疲れてるなこれ。それで $\left( \begin{array}{c} x_t \\ y_t \end{array} \right)$ が多変量正規分布にしたがったら何なの？

モーメント母関数の計算から、 $\left( \begin{array}{c} x_t \\ y_t \end{array} \right)$ のしたがう多変量正規分布は以下になることがわかります。

$\displaystyle \exp \left\{ -\frac{1}{2} \left( \begin{array}{c} x_t - \mu_{t|t-1} \\ y_t - H_t \mu_{t|t-1} \end{array} \right)^{\top} \left( \begin{array}{cc} V_{t|t-1} & V_{t|t-1}H_t^{\top} \\ H_t V_{t|t-1} & H_t V_{t|t-1} H_t^{\top} + R_t\end{array} \right)^{-1} \left( \begin{array}{c} x_t - \mu_{t|t-1} \\ y_t - H_t \mu_{t|t-1} \end{array} \right) \right\}$ つまり、分散共分散行列 $\Sigma$ が以下になります（ $A, \, B, \, C, \, D$ は $V_{t|t-1}$ などとサイズが合うように $\Sigma$ をブロックに分けた行列とします）。 $\Sigma = \left( \begin{array}{cc} A & B \\ C & D \end{array}\right) = \left( \begin{array}{cc} V_{t|t-1} & V_{t|t-1}H_t^{\top} \\ H_t V_{t|t-1} & H_t V_{t|t-1} H_t^{\top} + R_t \end{array} \right)$ さて、ここで時刻 $t$ の観測値 $y_t$ が得られたとしましょう。 $y_t$ を観測したもとでの $x_t$ の分布はどうなるでしょうか？つまり、上の式から「 $x_t$ の分散共分散行列」だけを切り出したいということです。もちろん $V_{t|t-1}$ は不正解です。分散共分散行列は逆行列の形で挟まっているので、分散共分散行列から左上の $n \times n$ のサイズのブロックを切り出せばいいということにはなりません（精度行列であればそれでいいんですが）。

元々 $x_t$ の分散共分散行列が $V_{t|t-1}$ であったはずなのになぜ $V_{t|t-1}$ にならないのか疑問に思う方もいるかもしれません。 $V_{t|t-1}$ は $y_t$ を知らない下での $x_t$ の分散共分散行列です。 $y_t$ を知ってしまうと分散共分散行列は変わってきます。斜めに傾いた（独立でない）2変量正規分布を思い浮かべて、それの横軸を $x_t$ 、縦軸を $y_t$ と考えてみてください（この記事のグラフの真ん中のようなイメージです）。もし $y_t$ について何も知らないなら、 $x_t$ の分布はこの2変量正規分布を $y_t$ 方向に積分することになります（先ほどの記事の Histgram of x）。しかし、ある $y_t$ を手に入れてしまった場合は、その値に引いた水平線で2変量正規分布を切った断面になります。グラフの上の方の値なのか、下の方の値なのかで $x_t$ の広がりは異なりますよね。 $y_t$ を観測したもとでの $x_t$ の分布を得るには、「2変量正規分布からの切り出し」が必要なんです。

後で気付いたんですが、PRML 下巻20ページの図 6.7 に $t_1, \, t_2$ の分布を $t_1$ で固定したときの $t_2$ の分布を示すイラストがありますね。

確かに逆行列だから単純に左上のブロックを取るわけにはいかないな。って、あれ？ $y_t$ を観測した下での $x_t$ の分布って、それフィルタ後分布じゃん。じゃあフィルタ後分散共分散行列はさっき上で求めたこれだろ？

$V_{t|t} = ({V_{t|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t)^{-1} = V_{t|t-1} - V_{t|t-1} {H_t}^{\top} (H_t V_{t|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t|t-1}$

さすがにばれてしまいましたか。その $V_{t|t}$ を $\Sigma$ の部分行列 $D$ に関するシューア補行列（Schur complement matrix）といいます。 $A, \, B, \, C, \, D$ でかくと $A - B D^{-1} C$ ですね。

へ？シュ、シューア補行列？何それ？確かに $V_{t|t}$ の式と $A, \, B, \, C, \, D$ を見比べると $A - B D^{-1} C$ になってるけど。

シューア補行列とは「ある行列に対して、その行列の逆行列の左上のブロックをとって、その逆行列を取ったもの」ですよ（あるいは右下のブロックでもよく、その場合は $A$ に関するシューア補行列 $D - C A^{-1} B$ となる）。上の多変量正規分布からの切り出しは、「一部の変数を固定した残りの変数のみの分散共分散行列を知りたいので、もとの分散共分散行列の逆行列をとって、その左上のブロックをとって、それの逆行列をとって分散共分散行列に戻したい」ということなので、これはシューア補行列そのものです。ちなみにシューア補行列を用いた逆行列のブロック表示からの Sherman-Morrison-Woodbury の公式の証明が参考文献にあるので参照してください。

ふーん？でもさっきカルマンフィルタを解いたときにシューア補行列なんて出てきた？出てきたのは Sherman-Morrison-Woodbury の公式じゃなかった？

そうなんですよね。こちらの解き方ではシューア補行列は出てきますが Sherman-Morrison-Woodbury の公式は出てきません。プロデューサーさんは Sherman-Morrison-Woodbury の公式は、カルマンフィルタの場合に限らず「多変量式分布の一部の変数を固定する場合」に適用できるのではないかと考えて、カルマンフィルタをそのようにとらえたかったようなんですが、そもそもこうやって解く場合は逆行列が出てこなかったんですよね。

駄目じゃん！

ただ、カルマンフィルタ同様、多変量正規分布どうしの積を平方完成するときは Sherman-Morrison-Woodbury の公式を適用する余地があると思います。

じゃあ、代わりに出てきたシューア補行列っていうのは？

いま出てきた通り、「多変量式分布の一部の変数を固定する場合」に、条件付き分散共分散行列を求めるのにつかいます。これは計算コストのための書き換えなどではなくて、表式を導くのに必要です。詳しくは PRML 上巻の 2.3.1 節を参照してください。そして、「多変量式分布の一部の変数を固定する」ことになる例の一つが「ガウス過程回帰」（PRML 下巻 6.4.2 節）です。

つづかない

2018-12-05

パターン認識と機械学習下（第6章：その4）

本読み機械学習

以下の本を読みます。上巻を読むこともあります。何か問題点がありましたらご指摘いただけますと幸いです。

パターン認識と機械学習下 (ベイズ理論による統計的予測)

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/02/29
メディア: 単行本
購入: 6人クリック: 14回
この商品を含むブログを見る

前回：その3 ／次回：まだ

結局等価カーネルというのは、線形基底関数モデルの重みパラメータをベイズ的に解いたときの、重みパラメータの事後分布の平均ベクトルによる、ある対象の点における予測値が、訓練データ中の各被説明変数の線形結合になっているという見方をすることができて、そのような見方をしたときに各被説明変数にかかる重みが、対象の点とその訓練データ点の「等価カーネル」なんですね。…この等価カーネルと 6.1 節のカーネル関数は異なるものですね。等価カーネル $k(x, x')=\beta \phi(x)^{\top} S_N \phi(x')$ は特徴の内積ではなく間に重みパラメータの事後分散共分散行列 $S_N$ を挟んでいますし。しかし $\psi(x) \equiv \beta^{1/2} S_N^{1/2} \phi(x)$ と新しい特徴を定義すれば等価カーネルはこの新しい特徴の内積にはなっていますね。

あれ？ジュン今ドイツじゃないの？

それは…これはテレビ電話です。

そこまでして勉強会してる設定なの俺たち！？

6.3.1 節の Nadaraya-Watson モデル（カーネル回帰）のシチュエーションは、点 $x$ における値が $t$ である同時分布 $p(x,t)$ を、各データ点から $x-x_n$ 離れた点における値が $t-t_n$ である同時分布 $f(x-x_n,t-t_n)$ の混合分布で表そうとしていますね。これも Parzen 推定法なんですね。Parzen 推定法は密度推定の方法であって回帰というイメージではありませんでしたが…しかし、被説明変数 $t$ を説明変数 $x$ 側にくっつければ回帰問題を密度推定問題ととらえることもできそうですね。

「 $f(x,t)$ の $t$ についての平均は零であるとする」っていうのは、ここでは $x$ をある点に固定したとき $t$ が $t_n$ を中心にした1次元の正規分布（例えば）みたいな分布になっているのを想定してるってことだよな。…じゃあ結局1つ1つの $f(x-x_n, t-t_n)$ については $t=t_n$ のところでの確率密度が一番大きくて、ある $x$ における $y(x)$ がどうなっているかは $f(x-x_n, t-t_n)$ の形が $x$ 方向にどうなっているかによるけど、 $x_n$ から離れるほど小さくなるような密度だったら、結局その $x$ に一番近い $x_n$ に対応する $t_n$ の影響を一番色濃く受けることになって…それって等価カーネルと似てるな。それに (6.45) 式も (3.61) 式と同じ形だ。でも今は線形基底関数モデルをベイズ的に解いたわけじゃないのになんで答えの形が同じになるの？

…6.3.1 節では最初から $t$ 方向にも $x$ 方向にもばらつきをもつ分布を混合しようとして自然に式 (6.45) の形が出てきたようにみえます。どちらかというと 3.3 節の結果が式 (3.61) の形になる方が直感的ではない気がしますが…。ただ式の形はともかく、やりたいこととしては、3.3 節で重みパラメータを分布として考えたのは結局 $t$ 方向のばらつきを考慮した回帰をしたい、ということになると思います。6.3.1 節で密度推定をしているのも同じだと思います。結局知りたいのは各点での $p(t|x)$ で、これを解くのに重みパラメータ $w$ を主役にするか各訓練データ点が張る密度 $f(x-x_n, t-t_n)$ を主役にするかというだけの違いな気もします。ただこちらの 6.3.1 節の枠組みでは分布の形 $f$ を等方的なガウシアンではなく柔軟に選択できると。いきなり分布の形を顕わにもつ (6.42) 式を仮定として出発しているのでそれはそうですね。…また 6.3 節冒頭に戻ると、(3.61) 式、(6.45) 式に加えてもう一つ同様の形の (6.40) 式が登場していて、これは (6.39) 式から出発して導かれたものですね。まとめると、以下のケースではすべて結果の回帰モデルが「各訓練データ点における被説明変数の値を、各訓練データ点との距離のRBFで混合したもの」になるんですね。

線形基底関数モデルを、重みパラメータの分布を事前分布から事後分布にベイズ的に更新するやり方で解いたときの、事後分布の平均値による解（3.6.1節）。
入力変数側にノイズが含まれる回帰モデルを変分法で解いたときの解（6.3節冒頭）。
同時分布を Parzen 推定したときの、各点における被説明変数の期待値（6.3.1節）。

RBF で混合する解になったということは「 $x_n$ に近い点での値は $t_n$ に近い値であるべき」という結論になったということですが、上の3つのケースのそれぞれ「重みパラメータの分布」「入力変数のノイズ」「説明変数と被説明変数の同時分布への仮定」がその由来になっていると思います。逆に、訓練データとして説明変数と被説明変数の組を与えられても、それだけでRBFを混合した解にはなりませんね。線形基底関数モデルを最小2乗法で解くことができる場合なら (6.9) 式の形にはなりますが、これはそもそも $t_n$ をカーネル関数の重みで混合した形をしていませんし。

ふーん…まあそれで13ページの下の方にさ、「より一般的には、同時分布 $p(t,x)$ を混合ガウス分布で表すことも可能であり」ってあるけど、そもそも (6.42) 式って $f$ がガウシアンなら混合ガウス分布じゃん。何言ってんのこれ？あと9章ぱらぱら見ても「9章で紹介するテクニック (Ghahramani and Jordan, 1994)」がどれのことかわかんなかった（見落としたかもだけど）…。

一瞬わかりにくいですよねここ…次のページまで読むと、ここで「混合ガウス分布で表す」といっているのは各訓練データの周りに密度を張ることではなくて、訓練データをEMアルゴリズムである程度混合ガウス分布にクラスタリングして、クラスタ単位で密度を張るという意味ですね。「9章で紹介するテクニック」のくだりは「9章で紹介するEMアルゴリズムを用いてクラスタリングしてからカーネル回帰する」ということだと思うんですが…Ghahramani and Jordan, 1994 自体は 9.3 節に関係していそうですが…。

まあいっか。結局 6.3 節の話って、この節に紹介されているようなケースだと RBF 型の等価カーネルの重みで訓練データ中の被説明変数の値を混合する形の答えになる、ってだけだよな…。ただここにきて初めて、カーネル関数の形に理由がついたってことなのかな。6.2 節までの時点ではどのカーネル関数を選ぶといいのかの理由って「このカーネル関数なら上手く学習できるかも？」くらいしかなかった気がするし…。といっても等価カーネルって 6.1 節で最初に紹介されたカーネル関数とはなんか違う（素直な特徴の内積じゃない）からちょっと引っかかるけど…。それで 6.4 節の「ガウス過程」もこれたぶんカーネル関数への理由づけだよな。6.4.1 節は「線形回帰再訪」？なんかさっきちらって見た9章にも「混合ガウス分布再訪」ってあったし、再訪しまくってんな…。

いいじゃないですか何度訪ねても。そうでなくても訪ねなければ忘れてしまいますし。

いや悪くないけど、「カーネル関数はあなたがすでに知っている問題にも現れる、こんなにも正当なものなんですよ」って話より、早くカーネル関数特有のすごい話みたいなのを聞きたいんだけど…。それで 6.4.1 節の問題設定は 3.3 節と同じだな。でも $y(x_1), \cdots, y(x_N)$ の同時分布を考えようとしてる…え、これらを並べたベクトルってガウス分布にしたがうの？

(6.51) 式ってこうですよね。それぞれ独立に多変量正規分布にしたがうベクトルを足し合わせた形をしていますから、 $y$ も多変量正規分布にしたがうんじゃないですか。

$\displaystyle y = \left( \begin{array}{c} w_1 \phi_1(x_1) + w_2 \phi_2(x_1) + \cdots + w_M \phi_M(x_1) \\ w_1 \phi_1(x_2) + w_2 \phi_2(x_2) + \cdots + w_M \phi_M(x_2) \\ \vdots \\ w_1 \phi_1(x_N) + w_2 \phi_2(x_N) + \cdots + w_M \phi_M(x_N) \end{array} \right)$ ほら、以下などに互いに独立な多変量正規分布にしたがう確率ベクトルの和は多変量正規分布にしたがうとかいてありますよ。

なるほど。それで…え、 $E[y]=0$ になっちゃうの？回帰モデルで「どこの点でも答えの期待値はゼロです」っておかしくない？ …って、 $w$ がまだ事前分布 $p(w)=N(w|0, \alpha^{-1}I)$ だからか。重みの平均がゼロならそりゃ回帰される値はゼロになるよな。それで、これがガウス過程？ガウス過程って確率過程の一種だよな？確率過程ってなんか時間変化していくような確率変数のことじゃないの？ウィキペディアにもそうかいてあるし。いまどこに時間変化要素あったの？？

確率過程 - Wikipedia

「時間変化していく」というのは確率過程の定義に含まれていません。だいたい確率過程の定義は数学の話ですし、数学の世界に時間という概念などないでしょう？確率変数の添え字は添え字であって、時間を意味している必要はありません。もちろん実際の応用では時間変化する対象を記述しようとして、時間の経過を添え字に背負わせることが圧倒的に多いわけですが…。ともかくここでは「 $x_1, \cdots, x_N$ をどのように選んでも $y(x_1), \cdots, y(x_N)$ の同時分布が多変量正規分布にしたがう」ことをガウス過程といっているにすぎません。なお、多変量正規分布の平均ベクトルと分散共分散行列は常に同じである必要はありません。ここでは平均ベクトルは常にゼロベクトルになりますが、分散共分散行列は (6.53) ですから $x_1, \cdots, x_N$ によって変わりますね。そしてこの分散共分散行列は、各成分が訓練データ点 $x_n$ と $x_m$ のカーネル関数になっています（正確にはそれに重みパラメータの事前分布の分散をかけたものですが）。「これらの訓練データ点上での値がどうなるか特徴で回帰したいが、まだ何も値を観測していないというとき、値はこれくらいの不確かさ（分散共分散行列）で広がっている」というのを出すと、カーネル関数が現れたということなんですね。他方、特徴は直接現れていません。

ふーん…まあガウスカーネルだったら近い点どうしは大きい値に（共分散大）、遠い点どうしは小さい値に（共分散小）なるわけで、じゃあこの分散共分散行列は、「まだ全然どんな値になるかわからなくて不確かだけど、近い点どうしだったら不確かさも同じ方向に広がっているだろ」「遠い点どうしだったら全然関係ないだろ」って感じなのかな…だから何って感じだけど…。で、この図 6.4 は何？本文には「ガウス過程からのサンプル」ってあるけど、説明足りなさすぎない？本文でいうどの式をプロットしてるの？？グラフにはちゃんと縦軸と横軸は何かかきましょうって習わなかったの？？

いきなり図だけだとわかりにくいですね…あ、描けました。

f:id:cookie-box:20181205224243p:plain:w320

f:id:cookie-box:20181205232147p:plain:w320

うおおいどうやって描いたんだよそれ！？

すみません、ぶっちゃけ以下にあったスクリプトを丸々コピーして実行しました…刊行に先立って意見を募集されているということなので、何か意見をお送りできるように善処します…。

MLPシリーズ『ガウス過程と機械学習』サポートページ

何その本！？めっちゃわかりやすそう！！

ともかくこれでわかりましたが、図 6.4 を描く方法は、例えば $x_1 = -1, \cdots, x_{100}=1$ と-1～1の点を均等に100点でもとって、それらの点から (6.54) 式にしたがって 100×100 次元のグラム行列を生成、それを分散共分散行列とした多変量正規分布から1点をサンプリングしたもの $y_1, \cdots, y_{100}$ をプロットしているだけです（1点といっても100変量正規分布からサンプリングした点なので100次元ですね）。100変量正規分布にしたがう乱数ベクトルを1つ生成してプロットしたものが赤色のグラフで、同じ分布からもう1回乱数ベクトルを生成してプロットしたものが青色のグラフで、…といった具合です。もし100変量正規分布の異なる成分間が独立であったらホワイトノイズのようなグラフになってしまいますが（分散の大きさが各点で同じなら実際ホワイトノイズですが）、そうではなく各成分がカーネル関数であるような分散共分散構造をもっているので、近い点どうしは近い値に＝滑らかになるわけです。指数カーネルの場合はちょっとギザギザしますけど。

ああこれ折れ線グラフだけど横軸方向に点がめっちゃいっぱいあって滑らかに見える感じなのか…てっきり何か関数の重ね合わせ的なのかと…。

本当はいくらでも密になるんだと思うんですが…。それはさておき、14ページの 6.4 節の冒頭にあった、「関数 $y(x,w)$ に関する事前分布」というのがこの色々な色のグラフたちの上の分布なんですね。100変量正規分布からもっとたくさんの点をサンプリングすれば「関数の分布」らしさが出るでしょうか。

f:id:cookie-box:20181205233338p:plain:w320

ごちゃごちゃしすぎ！！

（次回があれば）つづく