以下の本を読みます。上巻を読むこともあります。何か問題点がありましたらご指摘いただけますと幸いです。

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/02/29
- メディア: 単行本
- 購入: 6人 クリック: 14回
- この商品を含むブログを見る


あれ? ジュン今ドイツじゃないの?

それは…これはテレビ電話です。

そこまでして勉強会してる設定なの俺たち!?

6.3.1 節の Nadaraya-Watson モデル(カーネル回帰)のシチュエーションは、点 における値が
である同時分布
を、各データ点から
離れた点における値が
である同時分布
の混合分布で表そうとしていますね。これも Parzen 推定法なんですね。Parzen 推定法は密度推定の方法であって回帰というイメージではありませんでしたが…しかし、被説明変数
を説明変数
側にくっつければ回帰問題を密度推定問題ととらえることもできそうですね。

「 の
についての平均は零であるとする」っていうのは、ここでは
をある点に固定したとき
が
を中心にした1次元の正規分布(例えば)みたいな分布になっているのを想定してるってことだよな。…じゃあ結局1つ1つの
については
のところでの確率密度が一番大きくて、ある
における
がどうなっているかは
の形が
方向にどうなっているかによるけど、
から離れるほど小さくなるような密度だったら、結局その
に一番近い
に対応する
の影響を一番色濃く受けることになって…それって等価カーネルと似てるな。それに (6.45) 式も (3.61) 式と同じ形だ。でも今は線形基底関数モデルをベイズ的に解いたわけじゃないのになんで答えの形が同じになるの?

…6.3.1 節では最初から 方向にも
方向にもばらつきをもつ分布を混合しようとして自然に式 (6.45) の形が出てきたようにみえます。どちらかというと 3.3 節の結果が式 (3.61) の形になる方が直感的ではない気がしますが…。ただ式の形はともかく、やりたいこととしては、3.3 節で重みパラメータを分布として考えたのは結局
方向のばらつきを考慮した回帰をしたい、ということになると思います。6.3.1 節で密度推定をしているのも同じだと思います。結局知りたいのは各点での
で、これを解くのに重みパラメータ
を主役にするか各訓練データ点が張る密度
を主役にするかというだけの違いな気もします。ただこちらの 6.3.1 節の枠組みでは分布の形
を等方的なガウシアンではなく柔軟に選択できると。いきなり分布の形を顕わにもつ (6.42) 式を仮定として出発しているのでそれはそうですね。…また 6.3 節冒頭に戻ると、(3.61) 式、(6.45) 式に加えてもう一つ同様の形の (6.40) 式が登場していて、これは (6.39) 式から出発して導かれたものですね。まとめると、以下のケースではすべて結果の回帰モデルが「各訓練データ点における被説明変数の値を、各訓練データ点との距離のRBFで混合したもの」になるんですね。
- 線形基底関数モデルを、重みパラメータの分布を事前分布から事後分布にベイズ的に更新するやり方で解いたときの、事後分布の平均値による解(3.6.1節)。
- 入力変数側にノイズが含まれる回帰モデルを変分法で解いたときの解(6.3節冒頭)。
- 同時分布を Parzen 推定したときの、各点における被説明変数の期待値(6.3.1節)。



まあいっか。結局 6.3 節の話って、この節に紹介されているようなケースだと RBF 型の等価カーネルの重みで訓練データ中の被説明変数の値を混合する形の答えになる、ってだけだよな…。ただここにきて初めて、カーネル関数の形に理由がついたってことなのかな。6.2 節までの時点ではどのカーネル関数を選ぶといいのかの理由って「このカーネル関数なら上手く学習できるかも?」くらいしかなかった気がするし…。といっても等価カーネルって 6.1 節で最初に紹介されたカーネル関数とはなんか違う(素直な特徴の内積じゃない)からちょっと引っかかるけど…。それで 6.4 節の「ガウス過程」もこれたぶんカーネル関数への理由づけだよな。6.4.1 節は「線形回帰再訪」? なんかさっきちらって見た9章にも「混合ガウス分布再訪」ってあったし、再訪しまくってんな…。

いいじゃないですか何度訪ねても。そうでなくても訪ねなければ忘れてしまいますし。




「時間変化していく」というのは確率過程の定義に含まれていません。だいたい確率過程の定義は数学の話ですし、数学の世界に時間という概念などないでしょう? 確率変数の添え字は添え字であって、時間を意味している必要はありません。もちろん実際の応用では時間変化する対象を記述しようとして、時間の経過を添え字に背負わせることが圧倒的に多いわけですが…。ともかくここでは「 をどのように選んでも
の同時分布が多変量正規分布にしたがう」ことをガウス過程といっているにすぎません。なお、多変量正規分布の平均ベクトルと分散共分散行列は常に同じである必要はありません。ここでは平均ベクトルは常にゼロベクトルになりますが、分散共分散行列は (6.53) ですから
によって変わりますね。そしてこの分散共分散行列は、各成分が訓練データ点
と
のカーネル関数になっています(正確にはそれに重みパラメータの事前分布の分散をかけたものですが)。「これらの訓練データ点上での値がどうなるか特徴で回帰したいが、まだ何も値を観測していないというとき、値はこれくらいの不確かさ(分散共分散行列)で広がっている」というのを出すと、カーネル関数が現れたということなんですね。他方、特徴は直接現れていません。


いきなり図だけだとわかりにくいですね…あ、描けました。

うおおいどうやって描いたんだよそれ!?

すみません、ぶっちゃけ以下にあったスクリプトを丸々コピーして実行しました…刊行に先立って意見を募集されているということなので、何か意見をお送りできるように善処します…。

何その本!? めっちゃわかりやすそう!!

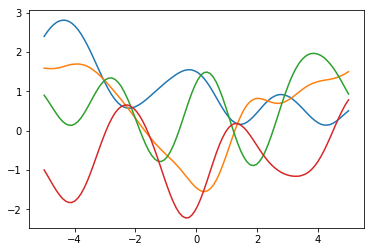
ともかくこれでわかりましたが、図 6.4 を描く方法は、例えば と-1~1の点を均等に100点でもとって、それらの点から (6.54) 式にしたがって 100×100 次元のグラム行列を生成、それを分散共分散行列とした多変量正規分布から1点をサンプリングしたもの
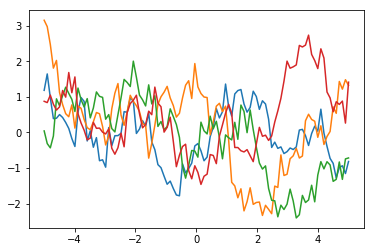
をプロットしているだけです(1点といっても100変量正規分布からサンプリングした点なので100次元ですね)。100変量正規分布にしたがう乱数ベクトルを1つ生成してプロットしたものが赤色のグラフで、同じ分布からもう1回乱数ベクトルを生成してプロットしたものが青色のグラフで、…といった具合です。もし100変量正規分布の異なる成分間が独立であったらホワイトノイズのようなグラフになってしまいますが(分散の大きさが各点で同じなら実際ホワイトノイズですが)、そうではなく各成分がカーネル関数であるような分散共分散構造をもっているので、近い点どうしは近い値に=滑らかになるわけです。指数カーネルの場合はちょっとギザギザしますけど。

ああこれ折れ線グラフだけど横軸方向に点がめっちゃいっぱいあって滑らかに見える感じなのか…てっきり何か関数の重ね合わせ的なのかと…。

本当はいくらでも密になるんだと思うんですが…。それはさておき、14ページの 6.4 節の冒頭にあった、「関数 に関する事前分布」というのがこの色々な色のグラフたちの上の分布なんですね。100変量正規分布からもっとたくさんの点をサンプリングすれば「関数の分布」らしさが出るでしょうか。


ごちゃごちゃしすぎ!!