以下の記事の続きです。Kerasブログの自己符号化器チュートリアルをやるだけです。
Keras で自己符号化器を学習したい - クッキーの日記
Kerasブログの自己符号化器チュートリアル(Building Autoencoders in Keras)の最後、Variational autoencoder(変分自己符号化器;VAE)をやります。VAE についてのチュートリアル上の説明は簡単なものなので、以下では自分で言葉を補っています。そのため、不正確な記述があるかもしれません。
変分自己符号化器(VAE)って何
そのデータが生成するメカニズムに仮定をおいているとき(そのデータの生成モデルを仮定しているとき)、モデルのパラメータの最適化をするのに VAE を用いることができます。今回は、「それぞれの手書き数字には、その手書き数字に対応する隠れ変数の確率分布があって、その分布からの実現値を変換することによって手書き数字ができている」と仮定しています。さらに、その隠れ変数の次元は2次元であって( )、隠れ変数の確率分布は2次元正規分布(
によってのみ決まる )と仮定しています。この分布からの実現値が
なる写像によって 784 ピクセルに変換されて目の前に手書き数字として具現化したのだと考えているわけです。


ここまでの自己符号化器では、入力と出力の交差エントロピーを損失関数としてモデルを訓練していました。VAE でも同様に訓練してもよいのですが、今回は入力と出力の交差エントロピーに、隠れ変数空間の事前分布と事後分布のKL情報量も加えたものを損失関数とします。つまり、隠れ変数の確率分布が大幅に更新されることに制約を課すわけですが、こうすることで、隠れ変数をきれいに( well-formed ? )モデリングでき、過学習も防げるそうです。
実行結果
今回、上図の VAE を MNIST の 60000 の訓練用データで学習しました(バッチサイズ:100、エポック数:10)。
テストデータについて、隠れ変数の確率分布の平均をプロットすると以下のようになりました。同じ数字のデータを同じ色でプロットしています。左上の濃い紫のかたまりが "0" です。左下のもう少し薄い紫のかたまりが "1" です。右下の黄緑色のかたまりは "7" です。同じ数字が隠れ変数空間上でかたまる傾向が確認できます。ただ、Kerasブログの元記事とは数字のかたまり方の形や配置が結構異なっています。
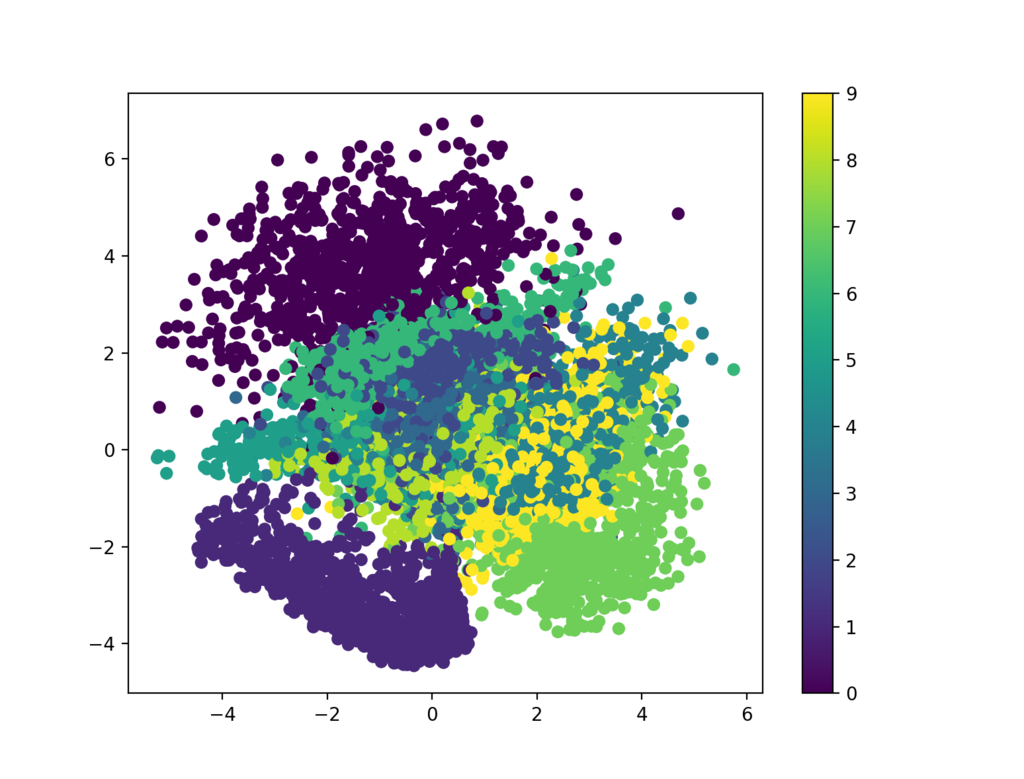
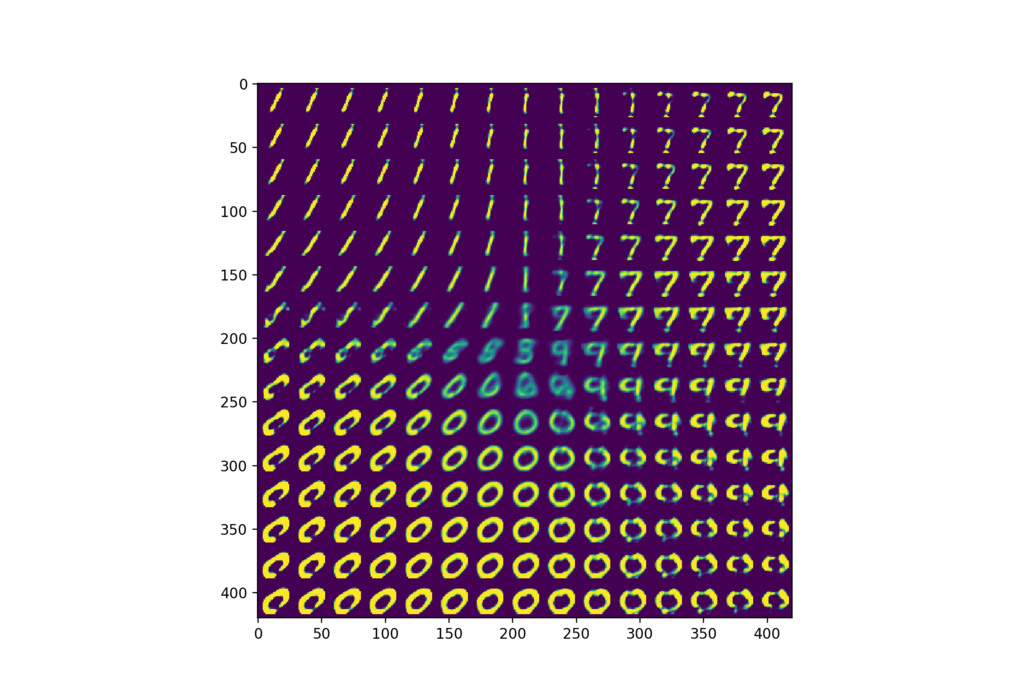
また、隠れ変数空間から均等にサンプリングした点がどんな「手書き数字」を生成するか(どうデコードされるか)というのも確かめることができます。以下のようになりました。実行したスクリプトの関係で上のプロットと上下が反転していますが、上のプロットと対応するように左上の方が "1"、右上の方が "7" に見えるのが確認できます。下の方は "0" に見えます。右側の真ん中あたりが "9" に見えますが、ちょうど上の図でも右側の真ん中あたりに "9" (黄色)が見えます。
スクリプト
補助関数の定義とクラスの定義を冒頭にもってきているのと日本語のコメントを加えている以外は以下にあるスクリプトと同じです。ただし、2番目のプロットはブログ記事のスクリプトと記述が違ったのでブログ記事の方に合わせています。
keras/variational_autoencoder.py at master · keras-team/keras · GitHub
# -*- coding: utf-8 -*- import numpy import matplotlib.pyplot as plt from scipy.stats import norm import sys from keras.layers import Input, Dense, Lambda, Layer from keras.models import Model from keras import backend, metrics from keras.datasets import mnist # 2次元正規分布から1点サンプリングする補助関数です def sampling(args): z_mean, z_log_var = args epsilon = backend.random_normal(shape=(batch_size, latent_dim), mean=0., stddev=epsilon_std) return z_mean + backend.exp(z_log_var / 2) * epsilon # Keras の Layer クラスを継承してオリジナルの損失関数を付加するレイヤーをつくります class CustomVariationalLayer(Layer): def __init__(self, **kwargs): self.is_placeholder = True super(CustomVariationalLayer, self).__init__(**kwargs) def vae_loss(self, x, x_decoded_mean): # オリジナルの損失関数 # 入力と出力の交差エントロピー xent_loss = original_dim * metrics.binary_crossentropy(x, x_decoded_mean) # 事前分布と事後分布のKL情報量 kl_loss = - 0.5 * backend.sum(1 + z_log_var - backend.square(z_mean) - backend.exp(z_log_var), axis=-1) return backend.mean(xent_loss + kl_loss) def call(self, inputs): x = inputs[0] x_decoded_mean = inputs[1] loss = self.vae_loss(x, x_decoded_mean) self.add_loss(loss, inputs=inputs) # オリジナルの損失関数を付加 return x # この自作レイヤーの出力を一応定義しておきますが、今回この出力は全く使いません if __name__ == "__main__": batch_size = 100 original_dim = 784 latent_dim = 2 intermediate_dim = 256 epochs = 10 epsilon_std = 1.0 #============================================================ # 変分自己符号化器を構築します # エンコーダ x = Input(batch_shape=(batch_size, original_dim)) h = Dense(intermediate_dim, activation='relu')(x) z_mean = Dense(latent_dim)(h) z_log_var = Dense(latent_dim)(h) z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var]) # デコーダ decoder_h = Dense(intermediate_dim, activation='relu') decoder_mean = Dense(original_dim, activation='sigmoid') h_decoded = decoder_h(z) x_decoded_mean = decoder_mean(h_decoded) # カスタマイズした損失関数を付加する訓練用レイヤー y = CustomVariationalLayer()([x, x_decoded_mean]) vae = Model(x, y) vae.compile(optimizer='rmsprop', loss=None) #============================================================ # モデルを訓練します (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train.astype('float32') / 255. x_test = x_test.astype('float32') / 255. x_train = x_train.reshape((len(x_train), numpy.prod(x_train.shape[1:]))) x_test = x_test.reshape((len(x_test), numpy.prod(x_test.shape[1:]))) vae.fit(x_train, shuffle=True, epochs=epochs, batch_size=batch_size, validation_data=(x_test, x_test)) #============================================================ # 結果を表示します # (1) 隠れ変数空間のプロット(エンコードした状態のプロット) encoder = Model(x, z_mean) # エンコーダのみ分離 x_test_encoded = encoder.predict(x_test, batch_size=batch_size) plt.figure(figsize=(6, 6)) plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test) plt.colorbar() plt.show() # (2) 隠れ変数空間からサンプリングした点がどんな手書き数字を生成するか(どうデコードされるか)をプロット decoder_input = Input(shape=(latent_dim,)) _h_decoded = decoder_h(decoder_input) _x_decoded_mean = decoder_mean(_h_decoded) generator = Model(decoder_input, _x_decoded_mean) # デコーダのみ分離 n = 15 # 15x15 個の手書き数字をプロットする digit_size = 28 figure = numpy.zeros((digit_size * n, digit_size * n)) grid_x = numpy.linspace(-15, 15, n) grid_y = numpy.linspace(-15, 15, n) for i, yi in enumerate(grid_x): for j, xi in enumerate(grid_y): z_sample = numpy.array([[xi, yi]]) x_decoded = generator.predict(z_sample) digit = x_decoded[0].reshape(digit_size, digit_size) figure[i * digit_size: (i + 1) * digit_size, j * digit_size: (j + 1) * digit_size] = digit plt.figure(figsize=(10, 10)) plt.imshow(figure) plt.show()