2017-02-19

これからの強化学習：ノート4

読んでいる本（出典）：これからの強化学習 | 牧野貴樹, 澁谷長史, 白川真一 |本 | 通販 | Amazon

この本読みですが、スライドにまとめようとしたら2回で挫折したのでとりあえず感想ノートの方を続けることにします。
というかどこまで読んだかもよくわからなくなりましたが、とりあえず落ち着いて現在の進捗を整理すると以下です。

テキスト範囲	読書メモ	スライド
1.1～1.3節（1～41ページ）	ノート1	勉強会#1
1.4～1.5節（42～70ページ）	まだ	勉強会#2
2.1節（71～111ページ）	ノート3	まだ
2.2～2.4節（112～147ページ）	この記事	まだ

以下、読書メモ。2章以降は1節1節が真面目に読むと重いのでふわっと雰囲気だけ。スライド作成時に補完したい。

2.2節

まず、強化学習にはさまざまな解法アルゴリズムがあるけど、アルゴリズムの性能を評価できないの？というお話。

1つの考え方としては、最善の選択をできた場合の収益に届かなかった分（リグレット）でもって評価する。
多腕バンディットタスクの場合、
- UCB1は、リグレットを $\varepsilon$ 減衰版 $\varepsilon$ -greedy を長期的に適用した場合よりも抑えられる。このアルゴリズムはゲーム木の探索やその他の探索問題にも応用できる。
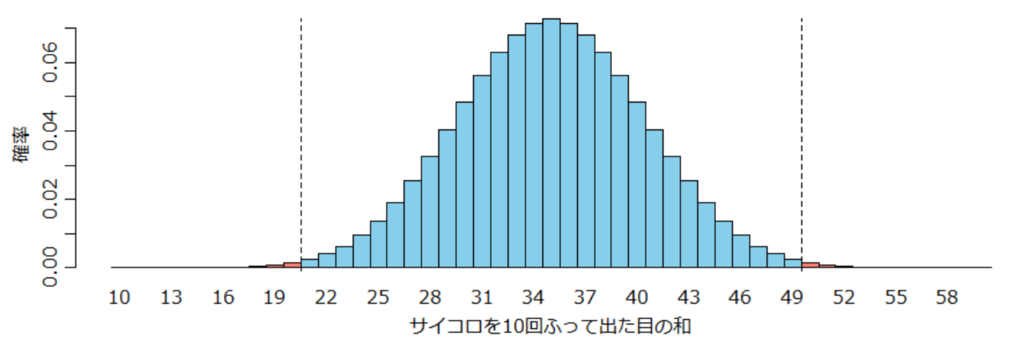
- Thompson サンプリング（下図；各腕を引いたときにコインが出てくる確率 $\mu$ の事後分布を更新していき、常にこの事後分布からのランダムサンプリング結果が最大の腕を選択する）でも「不確かなときは楽観的に」が実現でき、リグレットをUCB1と同等に抑えられる。
  
  ※ 確率分布の形は適当です。
別の考え方としては、間違った行動（最善の選択をした場合より期待収益が劣る行動）を取ってしまった回数で評価する（サンプル複雑性）。

あと、ちょうどUCB1や Thompson サンプリングで評価値の確率分布を更新していくように、探索と利用のトレードオフはベイズ的に取り扱えるよね、というお話。

ベイズ適応的マルコフ決定過程（BAMDP）という。

2.3節

報酬ってどう定義すればいいんだろう？というお話。

例えばボードゲームの学習で勝ったときにのみ +1 という報酬の定義はあり得るが、ゲームの性質が以下のような場合、このように終端状態のみで報酬を定義するのは得策ではない。
- 初期方策＝ランダムな手で勝てる見込みが薄い（そもそも学習が進まない）。
- 手数が多く、終端状態が初手の行動価値を修正する幅が小さい（学習が遅い）。
- 自分が勝ったとき、自分の行動と相手の行動のどちらが寄与したのか明らかにはわからない。
学習の結果を最善手に導いてくれるような報酬を定義したいんだけど、それなら最善手がわかっているときに、最善手が学習されるように（？）各状態に報酬を割り当てればいい（逆強化学習）。状態集合が有限集合なら、報酬関数の推定は線形計画問題になる。

2.4節

学習を速くしたいというお話。

経験強化型学習では、報酬を得たときに、前回報酬を得て以降に現れた状態行動対の評価値を更新する。このとき、エピソード内の各ステップの状態行動対に報酬からどれだけ過去かに応じてポイントを割り当て、そのエピソードにおけるある状態行動対の評価は、その状態行動対に割り当てられたポイントの和とする（その状態行動対を4回通れば4回分のポイントの和を取る：138ページの図2.4.1）。過去にさかのぼるほど等比減少関数でポイントを割り当てれば、迂回路となる状態行動対を優先してしまうことがない（ということか？）。
- Sutton本での単純なモンテカルロ法との違いは、単純なモンテカルロ法においては、ある状態行動対の評価はエピソード内の初回発生後の収益となるので、迂回路も平等に評価されてしまう。だからモンテカルロ法だと学習が遅い。ということだと思う。

「リグレットは『探索コスト』を表す指標に見えるが（113ページ）」：現実に「最善の選択をできた場合の収益」が出せないのは、現実には探索にコストをかける必要があるので、そのコストの分が差し引かれているように見える、という見方と考えられる。ただ、本当は、この箇所の直後に書かれているように、「探索と利用」から「探索」だけ切り離したようなものではない。
「探索と利用を同時に実現する（113ページ）」： UCB1は、どれだけ探索できているか（＝どれだけの精度で評価できているか）を加味して行動を選択するアルゴリズムだった（「これからの強化学習」勉強会#1 - クッキーの日記 7ページ）。その行動が未探索なほど（＝評価の精度が粗いほど）より高く評価するようにしておくことで、利用のために取った行動で探索（精度向上）も実現している。
Thompson サンプリング（114ページ）：フリーの原論文見つからず。以下のPDFが参考になる？
https://bandits.wikischolars.columbia.edu/file/view/Lecture+4.pdf
「（略）強化学習が優位な点としては、（略）たとえば、動的計画法のように環境のダイナミクスを表す状態遷移行列は不要であるし（127ページ）」：動的計画法が強化学習の範疇ではないような書き方なんだけど、動的計画法は強化学習の一解法だと思っていたんだけど、モンテカルロ法やTD学習による解き方のみを強化学習とみなすような線引きもあるということ？

2017-02-17

入門機械学習による異常検知―Rによる実践ガイド：ノート3

本読み機械学習

読んでいる本（出典）：入門機械学習による異常検知―Rによる実践ガイド | 井手剛 |本 | 通販 | Amazon

前回：ノート2 ／次回：まだ
目次：入門機械学習による異常検知―Rによる実践ガイド

読んだページ： 44～52ページ
以下、メモと雑談。

前回までのあらすじ

データが多次元正規分布にしたがう場合、で異常度を定義できる。
観測データが i.i.d. に多次元正規分布にしたがうなら、この異常度は F 分布にしたがう。
- 例．（ノート2と同じ例）2017年1月1日～18日の東京の最低／最高気温は、1.63±1.99℃／10.47±2.77℃だった。
  気象庁｜過去の気象データ検索
  このうち、2017年1月8日の東京の最低気温は1.6℃、最高気温は6.0℃だった。2017年1月8日は異常な日だったのだろうか。但し、ここで恣意的に、「14%も起こらないこと」を異常の閾値にする。
  → A. 最低気温と最高気温を1変数ずつみると異常ではないが、2変数の組合せは異常となる（以下）。
  - 2017年1月8日の最低気温だけみると1.6℃で、これはこの18日間の平均値1.63℃にかなり近いので異常値ではないだろう（証明略）。
  - 2017年1月8日の最高気温だけみると6.0℃とこの18日間で2番目に低いが、最高気温が独立同一正規分布にしたがうなら、「14%も起こらないこと」ではない（異常度 2.331211 < F分布の上側14%点 2.396771）。
    x1 <- c(2.0, 3.8, 3.5, 3.6, 3.7, 1.5, 0.1, 1.6, 3.8, 3.5, 3.9, 0.7, 1.4, -1.3, -2.3, -2.0, 0.7, 1.1)
    x2 <- c(13.8, 13.3, 13.7, 14.0, 10.4, 8.8, 8.7, 6.0, 11.1, 12.7, 11.0, 12.1, 12.7, 6.3, 4.7, 8.0, 10.9, 10.3)
    > a <- (18-1)/(18+1) * (x2[8]-mean(x2))^2 / (var(x2)*(18-1)/18)
    > a
    [1] 2.331211
    > F_0.14 <- qf(df1=1, df2=18-1, 0.86)
    > F_0.14
    [1] 2.396771
  - 2017年1月8日の最低／最高気温の組合せだと、最低／最高気温が独立同一2次元正規分布にしたがうなら、「14%も起こらないこと」といえる（F分布の上側14%点 2.228783 < 異常度 2.248451）。
    > mu <- colMeans(cbind(x1, x2))
    > xc <- cbind(x1, x2) - matrix(1, 18, 1) %*% mu
    > sigma <- t(xc) %*% xc / 18
    > a <- rowSums( (xc %*% solve(sigma) ) * xc)
    > a <- a * (18 - 2) / ((18 + 1) * 2)
    > a[8]
    [1] 2.248451
    > F2_0.14 <- qf(df1=2, df2=18-2, 0.86)
    > F2_0.14
    [1] 2.228783

なぜ異常度が F 分布にしたがうかという以前に、i.i.d. に次元正規分布にしたがう観測データからの、平均ベクトルと共分散行列の最尤推定値の導出の復習…。
- 対数尤度は。これをとについて偏微分しないといけない。
  - $\mu$ について偏微分するには、行列の積のトレースの微分公式 $\displaystyle \frac{\partial}{\partial A} {\rm Tr} (ABA^{\rm T}) = (B + B^{\rm T})A$ をつかうと $\displaystyle \frac{\partial L }{\partial \mu} = - \frac{1}{2} \sum_{n=1}^{N} \frac{\partial}{\partial \mu} {\rm Tr} \Bigl( (x_n - \mu)^{\rm T} \Sigma^{-1}(x_n - \mu) \Bigr) = - \Sigma^{-1} \sum_{n=1}^{N} (x_n - \mu)$
    （∵ 対称行列 $\Sigma$ は逆行列もまた対称なので、 $\Sigma^{-1} + (\Sigma^{-1})^{\rm T} = 2\Sigma^{-1}$ ）
  - $\Sigma$ について偏微分するには、正則な正方行列に関する微分公式 $\displaystyle \frac{\partial \ln |A|}{\partial A} = (A^{-1})^{\rm T}$ と、
    ベクトル $a$ と対称行列 $B$ について成り立つ $a^{\rm T} B a = \sum_i \sum_j b_{i,j} a_i a_j = {\rm Tr}(B a a^{\rm T})$ と、
    行列の積のトレースの微分公式 $\displaystyle \frac{\partial}{\partial B} {\rm Tr} (BA) = A^{\rm T}$ をつかうと
    $\displaystyle \frac{\partial L}{\partial (\Sigma^{-1})} = \frac{N}{2} \frac{\partial}{\partial (\Sigma^{-1})} \ln |\Sigma ^{-1}| - \frac{1}{2} \sum_{n=1}^{N} \frac{\partial}{\partial (\Sigma^{-1})} (x_n - \mu)^{\rm T} \Sigma^{-1}(x_n - \mu)$
    　　　　 $\displaystyle \, = \frac{N}{2} \Sigma - \frac{1}{2} \sum_{n=1}^{N} (x_n - \mu) (x_n - \mu)^{\rm T}$
それで、なぜ異常度が F 分布にしたがうのか（44～48ページ）。
- 証明の仕方は技巧的（47ページ）で、 $\displaystyle a(x') = \frac{(x' - \hat{\mu}) ^{\rm T} \Sigma ^{-1} (x' - \hat{\mu})}{(x' - \hat{\mu}) ^{\rm T} \Sigma ^{-1} (x' - \hat{\mu}) / (x' - \hat{\mu}) ^{\rm T} \hat{\Sigma} ^{-1} (x' - \hat{\mu})}$ とすると分子も分母もカイ2乗分布にしたがうので、全体はF分布にしたがう、という仕組み。
- 分母がカイ2乗分布にしたがう説明：「分母は。もともと自由度 $N-1$ のウィシャート分布にしたがう $M \times M$ 行列を、ブロック分割行列の逆行列の公式（付録の定理 A.4 参照）を使って $1 \times 1$ 行列に縮約したものに対応している（48ページ）」とあるけど、定理 A.4 を参照してもここの意味がよくわからない…。なぜ逆行列の公式で縮約ができるのか…。線型代数は大学で習ったけどもう覚えていなかった…。
- ウィキペディアには証明はなかった…原論文へのリンクは有。
  - Hotelling's T-squared distribution - Wikipedia

今回のお話

多次元のホテリング理論で「最高／最低気温の組合せが異常」というのは検知できるが、もっといえば、最高気温と最低気温のどちらが／あるいは両方が異常だったのかも知りたい。→ 正常であることが期待されるデータ群から、全データの1変数あたりのマハラノビス距離を計算し、ここまでが正常という閾値を適当に決め、異常なデータの1変数あたりのマハラノビス距離をこの閾値と比較する。
- 例．各都道府県の最低賃金、合計特殊出生率、高齢化率についてみてみる。
  最低賃金：地域別最低賃金の全国一覧｜厚生労働省
   合計特殊出生率：出生率、沖縄が1.94でトップ 46都道府県で上昇：日本経済新聞
  高齢化率：第1章高齢化の状況｜平成27年版高齢社会白書（概要版） - 内閣府
  これらのデータをつかっているのは、教科書と違う例で、乱数でなく親しみをもてる（？）データをつかってみたいというだけで、きっとモデルは適切ではないし、これで何か主張するということでは全くないです。
  最低賃金が平成27年度、合計特殊出生率は2015年、高齢化率は平成26年のデータを参照しています。
  - 上記のデータをプロットすると以下。
    等高線は2次元に周辺化したときの確率密度分布の等高線。既にこの時点で異常っぽい東京都、神奈川県、沖縄県にはラベルを付けてある。
  - 1変数あたりのマハラノビス距離を求める。やはり東京、神奈川、沖縄の値は大きい。閾値は2.5くらいにする。すると宮城と島根も閾値に引っかかる。閾値に引っかかった都道府県のデータは以下。
```
        pref wage birth aging
4     Miyagi  726  1.31 0.246
13     Tokyo  907  1.17 0.225
14  Kanagawa  905  1.34 0.232
32   Shimane  696  1.80 0.318
47   Okinawa  693  1.94 0.190
```
  - これらの都道府県のSN比解析は以下。SN比が正に大きい変数が異常度に寄与している。
    上の図とも合わせて、例えば沖縄は明らかに合計特殊出生率が高く、高齢化率が低い。
    宮城は、SN比でみると合計特殊出生率が最も異常度に寄与している。でもそのSN比も突出して大きくはない。上の図とも合わせると、宮城の3変数の組合せの異常度が大きくなっている要因は、「同じような最低賃金の水準の都道府県の中では合計特殊出生率が低い」「同じような最低賃金水準の都道府県の中では高齢化率が低い」というところにありそう。

2017-02-13

数理論理学：ノート4

本読み数理論理学

読んでいる本（出典）：数理論理学 | 戸次大介 |本 | 通販 | Amazon

前回：ノート3 ／次回：まだ
目次：数理論理学

以下、第5章後半の自分の理解。
最後の節（標準形）がまだ読めていないので、後でこの記事に加筆するか、新しい記事にまとめる。

前回までのあらすじ（一階述語論理の統語論）

命題論理では扱えない「すべての $x$ について～」「ある $x$ が存在して～」のような知見を表現すべく、論理式を名前と述語に分けます。
$\forall$ や $\exists$ といった量化子を導入します。
論理式がすごい増えてしまいそうですが、自然数で番号付けできます（ゲーデル数）。
- 但し、論理式のパーツになる記号の集合 $\mathcal{A}$ は高々可算集合とする。

一階述語論理の意味論

命題論理のときと同様、「論理式の集合真偽の領域」であるような解釈を考える。
命題論理のときは、は「原子命題の真偽の組合せの全パターン」ということで原子命題の数個あった。
一方、一階述語論理では原子命題がさらに項と述語に分かれるので、「各項が指し示しているもの」「各述語について、項が指し示しているものに対応する、論理式の真偽」として考えるのがよい（構造）。
あと変項もあるので、変項に何を割り当てたかも論理式の真偽にかかわる（割り当て ）。
つまり、ある1つの解釈を与えるには、以下を完全に決めればよい。
- そもそもどんなものたちについて命題を述べるのか（存在物）の集合： $D_M$
- 名前記号が指す存在物は何か： $F_M : \{ a_1, a_2, \cdots \} \to D_M$
- $n$ 個の存在物に $n$ 項演算子を適用したときに指す存在物は何か： $F_M : \{ o_{n,1}, o_{n,2}, \cdots \} \to {D_M}^{{D_M}^n}$
- $n$ 個の存在物に $n$ 項述語を適用したときの真偽はどうか： $F_M : \{ \theta_{n,1}, \theta_{n,2}, \cdots \} \to {D_t}^{{D_M}^n}$
- 変項に何を割り当てたか： $g : \{\xi_1 , \xi_2, \cdots \} \to D_M$

Ex．あるゲームのキャラクターたちについて命題を述べるとする（以下、ネタバレな上にしようもない例）。

　　 $M_1$ をダンガンロンパのキャラクターの構造とすると、 $D_{M_1}=\{$ 苗木誠, 舞園さやか, 桑田怜恩, $\cdots \}$ 。
　　名前記号から存在物への対応付けは例えば、 $F_{M_1}(a_1)=$ 苗木誠 , $F_{M_1}(a_2)=$ 舞園さやか , $\cdots$ 。
　　例えば $o_{1,1}(\tau_1)$ が「 $\tau_1$ を殺した犯人」のような1項演算子なら、 $F_{M_1}(o_{1,1})($ 舞園さやか $) =$ 桑田怜恩。
　　例えば $\theta_{2,1}(\tau_1, \tau_2)$ が「 $\tau_1$ は $\tau_2$ を殺した」のような2項述語なら、 $F_{M_1}(\theta_{2,1})($ 苗木誠, 舞園さやか $) = 0$ 。
　　このように、各名前記号が指す存在物、各 $n$ 項演算子が指す存在物（項が指す存在物による）、各 $n$ 項述語の
　　真偽（項が指す存在物による）を完全に決めれば、この論理体系のすべての基本述語の真偽は完全に決まる。

　　※ ここで、「桑田怜恩が舞園さやかを殺したから $F_{M_1}(o_{1,1})($ 舞園さやか $) =$ 桑田怜恩」ということではなく、
　　　あくまで $o_{1,1}(\tau_1)$ という1項演算子をこの写像で定義したということに注意。
　　※ ただ、 $o_{1,1}(\tau_1)$ が本当に「 $\tau_1$ を殺した犯人」になるように定義されていて、 $\theta_{2,1}(\tau_1, \tau_2)$ が本当に「 $\tau_1$ が
　　　 $\tau_2$ を殺した」かどうかを表すように定義されているなら、 $\theta_{2,1}(o_{1,1}(\tau_1), \tau_1)$ はどの解釈でも真になりそう。
　　　殺されていないキャラクターを代入したときの取り扱いは適切にする必要があるけど。

　　他方、別の解釈の下では、論理体系にはスーパーダンガンロンパ2のキャラクターの構造 $M_2$ が当てはめられて
　　いるかもしれない。 $D_{M_2}=\{$ 日向創, 七海千秋, $\cdots \}$ 。
　　この場合の名前記号の対応付けは例えば、 $F_{M_2}(a_1)=$ 日向創 , $F_{M_2}(a_2)=$ 七海千秋 , $\cdots$ かもしれない。

量化論理式の真偽を解釈するには、への割り当てをすべての存在物に変異させる（というより、これがという論理式の定義そのものである）。
- $\langle M, g \rangle (\forall \xi \varphi)=1 \; \Longleftrightarrow \;$ すべての $a \in D_M$ について $\langle M, g \rangle [ \xi \mapsto a] (\varphi) = 1$ である．
- $\langle M, g \rangle (\exists \xi \varphi)=1 \; \Longleftrightarrow \; \langle M, g \rangle [ \xi \mapsto a] (\varphi) = 1$ となる $a \in D_M$ が存在する．
解釈について、以下が成り立つ。
- その変項が項／論理式の自由変項でないなら、その変項を変異させても項が指す存在物／論理式の真偽は変わらない。
- 項／論理式の変項にある項を代入した上で解釈しても、解釈の割り当ての変異によって変項をある項に変えても、どちらの場合も項が指す存在物／論理式の真偽は変わらない。
- 項 $\tau_1$ と $\tau_2$ が指す存在物が同じなら、項／論理式の変項を $\tau_1$ に変異させても $\tau_2$ に変異させても項が指す存在物／論理式の真偽は変わらない（外延性）。

一階述語論理における妥当な推論

意味論的含意の概念は一階命題論理のときと同じ。
量化論理式が推論の前提 or 帰結になる場合に色々な定理が成り立つ。

練習問題5.48
$n$ 項述語に渡せる項のセットのパターン数は、 $|D_M|^n$ パターンある。
それぞれのパターンが1か0を取りうるので $n$ 項述語は $2^{|D_M|^n}$ 種類ありうる。
例えば、 $D_M =\{A_1, A_2\}$ で、 $n=2$ だったら、 $2$ 項述語 $\theta_{2, i}$ は16種類ある。

$\tau_1$	$\tau_2$	$\theta_{2,1}$	$\theta_{2,2}$	$\theta_{2,3}$	$\theta_{2,4}$	$\theta_{2,5}$	$\theta_{2,6}$	$\theta_{2,7}$	$\theta_{2,8}$	$\theta_{2,9}$	$\theta_{2,10}$	$\theta_{2,11}$	$\theta_{2,12}$	$\theta_{2,13}$	$\theta_{2,14}$	$\theta_{2,15}$	$\theta_{2,16}$
$A_1$	$A_1$	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0
$A_1$	$A_2$	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0
$A_2$	$A_1$	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0
$A_2$	$A_2$	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0

練習問題5.55

「奇数の二乗は奇数である」は真だが、 $\forall x ($ 奇数 $(x) \; \land$ 奇数 $(x \times x) \, )$ は、 $x$ に例えば $2$ を割り当てたとき偽。
「二乗が奇数であるような奇数が存在する」は真で、 $\exists x ($ 奇数 $(x) \to$ 奇数 $(x \times x) \, )$ も真だが、前者は $2$ を割り当てると偽で、後者は $2$ を割り当てても真（というか後者はどんな数を割り当てても真）。

練習問題5.58　面倒なので略。

練習問題5.60　面倒なので略。

練習問題5.62　面倒なので略。

練習問題5.65　面倒なので略。

練習問題5.82　面倒なので略。

練習問題5.84　面倒なので略。

練習問題5.86　面倒なので略。

練習問題5.88　面倒なので略。

練習問題5.90　面倒なので略。

練習問題5.91
$\forall x (F(x)) \land G(a) = \! \! \! | | \! \! \! = \forall x (\lnot \lnot F(x)) \land G(a)$ を証明するには、二重否定律より $F(x) = \! \! \! | | \! \! \! = \lnot \lnot F(x)$ なので、これに量化論理式の置き換えを用いて $\forall x (F(x)) = \! \! \! | | \! \! \! = \forall x (\lnot \lnot F(x))$ 。これと $G(a) = \! \! \! | | \! \! \! = G(a)$ に対し複合論理式の置き換えを適用。

所感

「 $x$ は哺乳類である」「 $x$ は卵生である」の変項 $x$ に「友達の鈴木君」を割り当てる（98ページ）：確かに友達の鈴木君は哺乳類だし、卵生ではないけど、鈴木君的には友達からの扱いが「哺乳類の一個体」でいいのだろうか…。
集合における外延性は、「集合はそれが含む要素によって一意に定まる」。外延性の公理 - Wikipedia
一階述語論理の解釈の外延性（定理5.64）は、「論理式の真偽は項が指す存在物によって一意に定まる」。当たり前に感じられすぎてよくわからない。「定義されたこと以外は知らないふりをする《知らないふりゲーム》」（数学ガールゲーデルの不完全性定理の31ページ）は、こと「ある論理式が真か偽か」については経験がありすぎるので難しい。
ラムダ計算（114ページ）って何。
- ラムダ計算 - Wikipedia

2017-01-19

入門機械学習による異常検知―Rによる実践ガイド：ノート2

本読み機械学習

読んでいる本（出典）：入門機械学習による異常検知―Rによる実践ガイド | 井手剛 |本 | 通販 | Amazon

前回：ノート1 ／次回：ノート3
目次：入門機械学習による異常検知―Rによる実践ガイド

読んだページ： 23～44ページ
以下、メモと雑談。

前回までのあらすじ

観測値の異常度は、正常なデータ群の分布に対する対数尤度で測るよ。
- 例．サイコロを10回ふって出た目の和が20以下か50以上になる確率は1%未満なので、もしサイコロをふった結果そうなってしまったらあまり尤もらしくなく、異常なのではないか（サイコロかあなたが）。
異常度の閾値をどう設定するべきかについて、観測データが i.i.d. に正規分布にしたがうなら、異常度が F 分布にしたがうよ（ホテリング理論）。
- 例．東京の2017年1月1日～18日の日ごとの平均気温は以下だった。気象庁｜過去の気象データ検索
  x <- c(7.4, 7.2, 8.0, 8.5, 6.7, 4.5, 4.1, 3.9, 7.2, 8.1, 6.9, 6.0, 6.2, 2.4, 0.7, 3.2, 5.4, 5.8)
  もし1月19日の平均気温が0℃だったら異常なのかどうか考える。日ごとの平均気温が i.i.d. に正規分布にしたがうと仮定するのは気象学的には駄目かもしれないけど、ここではいいことにして、「1% も起こりそうにないこと」を異常とみなすなら、0.30℃未満か 11.06℃超が異常になる。つまり、1月19日の平均気温が0℃なら異常である。
  > qnorm(mean=mean(x), sd=sqrt(var(x)*(18-1)/18), 0.005)
  [1] 0.2975372
  > qnorm(mean=mean(x), sd=sqrt(var(x)*(18-1)/18), 0.995)
  [1] 11.05802
  ただ、上の議論では、「1月1日～18日の平均気温は正規分布から歪んでいなかったのか」が考慮されていない。そもそも18点しかサンプルがないなら、平均や分散の推定値には区間幅があるだろう。それも考慮すれば、 $(x' - \hat{\mu})^2 / \hat{\sigma}^2 \sim (N+1)/(N-1) \cdot \mathcal{F}(1, N-1)$ が成り立つので（ホテリング理論）、以下のように正常と判定される範囲が少し広がり、-0.72℃未満か 12.08℃超が異常になる。つまり、1月19日の平均気温が0℃ならぎりぎり異常ではない。あまり0℃になってほしくはないけど。
  > F_0.01 <- qf(df1=1, df2=18-1, 0.99)
  > F_0.01
  [1] 8.39974
  > mean(x) - sqrt(var(x) * (18+1) / 18 * F_0.01)
  [1] -0.7220735
  > mean(x) + sqrt(var(x) * (18+1) / 18 * F_0.01)
  [1] 12.07763
  なお、各日の異常度とF分布上側1%の閾値ラインをプロットすると以下。1月1日～18日の平均気温に異常値はなかった。15日の日曜日は特に寒かったけど、異常ラインに達するほどではなかった。
- 1変数のホテリング理論の証明（26～36ページ）について。
  - 定理2.3（30ページ）は以下でも示せる。
    正規分布の二乗和がカイ二乗分布に従うことの証明 | 高校数学の美しい物語
  - 式2.26（33ページ）の ${\rm H}_N$ について、 ${\rm H}_N = {\rm H}_N^{\rm T}$ かつ ${\rm H}_N^2 = {\rm H}_N$ に注意。
  - 定理2.5（35ページ）を、教科書のやり方を追っていないけど自分でやってみる。
    $x \sim \chi^2(m, a), \; y \sim \chi^2(n, b)$ のとき、 $\displaystyle z \equiv \frac{x/(am)}{y/(bn)} \sim \mathcal{F}(m, n)$ を示せ。
    とりあえず分布の式をちゃんと書いておく。
    $\displaystyle f_X(x) = \frac{1}{2a \Gamma (m/2)} \left( \frac{x}{2a} \right) ^{m/2 -1} \exp \left( -\frac{x}{2a} \right)$
    $\displaystyle f_Y(y) = \frac{1}{2b \Gamma (n/2)} \left( \frac{y}{2b} \right) ^{n/2 -1} \exp \left( -\frac{y}{2b} \right)$
    $\displaystyle f_Z(z) = \frac{\Gamma (m/2 + n/2)}{\Gamma(m/2) \Gamma(n/2)} \left( \frac{m}{n} \right) ^{m/2} z^{m/2 - 1} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2}$
    $w=y, \; z=bnx/(amy)$ に変数変換する。 $x = amwz/(bn), y = w$ のヤコビアンは、
    $\displaystyle J(w, z) = \begin{vmatrix} amz/(bn) & amw/(bn) \\ 1 & 0 \end{vmatrix} = -\frac{amw}{bn}$
    $w, \; z$ の同時確率密度関数は、統計検定の教科書の22ページより、
    $f_{WZ}(w, z) = f_{XY}\bigl( amwz/(bn), \; w \bigr) \bigl| J(w, z) \bigr|$
    　　　　　 $\; \displaystyle = \frac{1}{2a \Gamma (m/2)} \left( \frac{mwz}{2bn} \right) ^{m/2 -1} \exp \left( -\frac{mwz}{2bn} \right) \cdot \frac{1}{2b \Gamma (n/2)} \left( \frac{w}{2b} \right) ^{n/2 -1} \exp \left( -\frac{w}{2b} \right) \cdot \frac{amw}{bn}$
    　　　　　 $\; \displaystyle = \frac{z^{m/2 -1}}{2b \Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \left( \frac{w}{2b} \right) ^{(m+n)/2 - 1} \exp \left( -\frac{w}{2b} \bigl( \frac{mz}{n} + 1 \bigr) \right)$
    $z$ の分布を出すには、これを $w$ について積分して周辺化すればよい。
    $\displaystyle f_Z(z) = \int_0^{\infty} dw f_{WZ}(w, z)$
    　　　 $\displaystyle \, = \frac{z^{m/2 -1}}{2b \Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \int_0^{\infty} dw \left( \frac{w}{2b} \right) ^{(m+n)/2 - 1} \exp \left( -\frac{w}{2b} \bigl( \frac{mz}{n} + 1 \bigr) \right)$
    　　　 $\displaystyle \, = \frac{z^{m/2 -1}}{\Gamma (m/2) \Gamma (n/2)} \left( \frac{m}{n} \right) ^{m/2} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2} \int_0^{\infty} dt \cdot t ^{(m+n)/2 - 1} \exp (-t)$
    　　　 $\displaystyle \, = \frac{\Gamma (m/2 + n/2)}{\Gamma(m/2) \Gamma(n/2)} \left( \frac{m}{n} \right) ^{m/2} z^{m/2 - 1} \left( 1 + \frac{mz}{n} \right) ^{-(m+n)/2}$
    なんかちゃんと出たからこれでいいや。

今回のお話

データが多次元正規分布にしたがう場合も、同様にで異常度を定義できる。
- これもマハラノビス距離の2乗。雑記 - クッキーの日記
- 例．東京の2017年1月1日～18日の最低／最高気温は以下だった。気象庁｜過去の気象データ検索
  x1 <- c(2.0, 3.8, 3.5, 3.6, 3.7, 1.5, 0.1, 1.6, 3.8, 3.5, 3.9, 0.7, 1.4, -1.3, -2.3, -2.0, 0.7, 1.1)
  x2 <- c(13.8, 13.3, 13.7, 14.0, 10.4, 8.8, 8.7, 6.0, 11.1, 12.7, 11.0, 12.1, 12.7, 6.3, 4.7, 8.0, 10.9, 10.3)
  どの日が異常っぽいというか、あまりまとまっていない…。
  
  とりあえず各日の異常度を求める。
  mu <- colMeans(cbind(x1, x2))
  xc <- cbind(x1, x2) - matrix(1, 18, 1) %*% mu
  sigma <- t(xc) %*% xc / 18
  a <- rowSums( (xc %*% solve(sigma) ) * xc)
  a <- a * (18 - 2) / ((18 + 1) * 2)
  th <- qf(df1=2, df2=18-2, 0.99)
  案の定、1%基準で異常ラインに達した日はなかった。特に寒かった15日よりも、上図においてデータ点が対角線から離れ気味の（最低気温と最高気温の差が他の日付に比べてかなり小さい）8日の方が異常度が微妙に大きかった。

2017-01-18

ゼロから作るDeep Learning：読了メモ

本読み深層学習

とてもわかりやすいという巷の評判に流されてこの本を読みました。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
斎藤康毅

オライリージャパン 2016-09-24
売り上げランキング : 58

Amazonで詳しく見る by G-Tools

一貫して読み手の理解を考慮して書かれたすばらしい本だと思います（その分トピックは絞られていますが）。
1章だけではなく最後まで・隅々までそれをやり切っている本というのが実はあまりないと思います。
モデルや手法の義務的な紹介にはなっておらず、伝えるべき心にたくさんページを割いていると思います。
これから深層学習を学ぶ人、ライブラリをつかうのでゼロから作るつもりはないという場合も、よほど中身はどうでもいい主義者でない限りよい本と思います。数式が苦手でない人には易しすぎると感じられる面もあるでしょうが、他のオムニバス本を読み解くより時短で要点を抑えられると思います。
説明が丁寧な分、CNN の話はありますが、RNN / 自己符号化器 / 制限ボルツマンマシンはありません（最終章に言葉のみ）。

以下、読んでいていいなあと思った箇所や自分なりの補足のメモです。

各章末にまとめ（「本章で学んだこと」）があり、各章の位置付けがわかりやすい。
要所要所で、そのアルゴリズムは全体図としてどんなステップからなるか確認している。
本のサブタイトルに「理論と『実装』」とあるように、実装する上での数値誤差等の注意・対策も抜かりない。実装が切り離されずすぐ傍にあるので、理論が一層理解しやすい。
まず、いきなり多層パーセプトロンの数学的モデルを説明するのではなく、なぜ多層化しないといけないのか、なぜ活性化しないといけないのかから入っている（2章）。
- つまり、入力データ空間が1枚の分離超平面で仕切れるなら多層化も活性化もしなくてよい。
- （以下は教科書の雑なアレンジ）例えば、2次元の入力データが4点あり、各点に "OK" / "NG" のラベルがついているとする。この4点を教師データに、未知の点の "OK" / "NG" を判定するニューラルネットを学習したいとする。
  下図の一番左のように、右上の3点が "OK" なら、1つの仕切りを入れられる。
  左から2番目のように、左下の3点が "OK" でも1つの仕切りを入れられる。
  ただし、左から3番目のように、左上と右下が "OK" だった場合、1つのまっすぐな仕切りではどうにもならない。仕切りを複数入れるか、仕切りをねじ曲げるかしないといけない。そうなると、1層パーセプトロン（入力データの線形変換しかできない）では対応できない。これが2層になると対応できる（下図一番右）。

f:id:cookie-box:20170117170802p:plain:w640

「2層のパーセプトロン（中略）を用いれば、任意の関数を表現可能であることが証明されています（36ページ）。」
- 原論文は以下の方の記事に詳しい。
  mathetake.hatenablog.com
2層ニューラルネット（隠れ層のノード数：50、隠れ層の活性化関数：シグモイド）の MNIST 認識精度（16エポック後）が、目算 95% 弱くらいか（121ページ）。
- 隠れ層なしの単層でも 92% くらい出るが（以下： TensorFlow チュートリアル）この差は大きい。
  https://www.tensorflow.org/tutorials/mnist/beginners/#softmax_regressions
誤差逆伝播法（5章）は、20ページ以上かけて絵本のように説明しているのでこの手法の意図がわかりやすい。
Momentum（171ページ）はハミルトニアンモンテカルロ法っぽい。Momentum は損失関数が小さい方へパラメータを転がす。HMC法では事後確率が大きい方へパラメータを転がす。
- 基礎からのベイズ統計学 Skype読書会(13)：参加メモ - クッキーの日記
Weight decay（193ページ）や Dropout（195ページ）で過学習を抑えられているけど汎化能力も上がっていないようには見える。
7章は CNN で、以下はもう教科書関係ないけど、最近見て面白かったアニメーションと、読んでおきたいサーベイ。
- GitHub - vdumoulin/conv_arithmetic: A technical report on convolution arithmetic in the context of deep learning
- Recent Advances in Convolutional Neural Networks
  https://arxiv.org/pdf/1512.07108v5.pdf

ただ、全体図の確認がなくても、章末にまとめがなくても、章末のまとめがまとめになっていなくても、自分でまとめるというのが勉強になるとは思う。とはいっても、あらゆる本をじっくり読む時間はないので。
「なぜ損失関数を設定するのか？（95ページ）」：この時点でこれが訊けるなら、質問力において魔界大冒険ののび太や数学ガールのユーリと張り合えますね。
微分の定義（97ページ）…今年のセンター試験…。