以下の論文を読みます。
Rajat Sen, Hsiang-Fu Yu, Inderjit S. Dhillon. Think Globally, Act Locally: A Deep Neural Network Approach to High-Dimensional Time Series Forecasting. In Advances in Neural Information Processing Systems 32, 2019.
https://papers.nips.cc/paper/8730-think-globally-act-locally-a-deep-neural-network-approach-to-high-dimensional-time-series-forecasting
https://papers.nips.cc/paper/8730-think-globally-act-locally-a-deep-neural-network-approach-to-high-dimensional-time-series-forecasting
※ キャラクターは架空のものです。解釈の誤りは筆者に帰属します。お気付きの点がありましたらご指摘ください。
次回:まだ

近年の時系列データには、一系列が一個人に対応し、何千もの系列が互いに相関するようなものがありうるとありますね。なのでそれらの系列からグローバルなパターンを搾り取った上で、個別データに対するキャリブレーションをするとよい予測ができるのではないかといっています。そこでこの論文で提案するモデル、DeepGLO は「グローバルな」Matrix Factorizartion モデルと、個別の系列の性質及びそれらの相関を捉えるネットワークを組み合わせるということです。
冒頭で時系列予測は様々な分野で重要な課題だといって挙げられている例は、1番上のは本論文と同じ Amazon の方々の論文で、2番目は割と古いですね。3番目も結構古い本です。
- Bayesian Intermittent Demand Forecasting for Large Inventories(retail demand forecasting)
- Financial time series forecasting using support vector machines - ScienceDirect(financial predictions)
- Amazon | Time-Series Forecasting | Chris Chatfield | Applied( predicting traffic or weather patterns)
それで、時系列予測は伝統的には個々の系列や少数の系列たちに対して AR、ARIMA、指数平滑法、Box-Jenkins法、状態空間モデルを適用する方法がとられてきたとありますね。このうち、状態空間モデルについては複数の系列を一緒に取り扱えますよね。しかし、膨大な数の系列にはスケールしないということですか。まあそんな気はしますが…。そして、すべての系列が共通にもっているパターンを上手く利用できないともあります。これは状態空間モデルでもそうなんでしょうか。よくわかりません。それらに対してニューラルネット手法として RNN、LSTM、WaveNet の話があって、これらは大規模な時系列も学習できるものの、2つの欠点があると指摘していますね。
- 個々の時系列の規模が異なると上手くいかない。例えば個々の製品の需要予測の場合、人気商品の需要の規模はニッチな商品のそれよりも大きい。このような場合、上記のようなニューラルネット手法では正規化が必要になる。しかし、正規化のパラメータ調整は難しい。
- モデルは予測時に個別のデータの過去データしか利用していない。しかし、データはすべての時系列にわたるグローバルなパターンをもっている。
- なので、これに対処したモデルも提案されている(後者は本論文と同じ方の論文ですが、このときは所属が Amazon ではないのですね)(前者はコードがありますが Python2.7 だと…)。
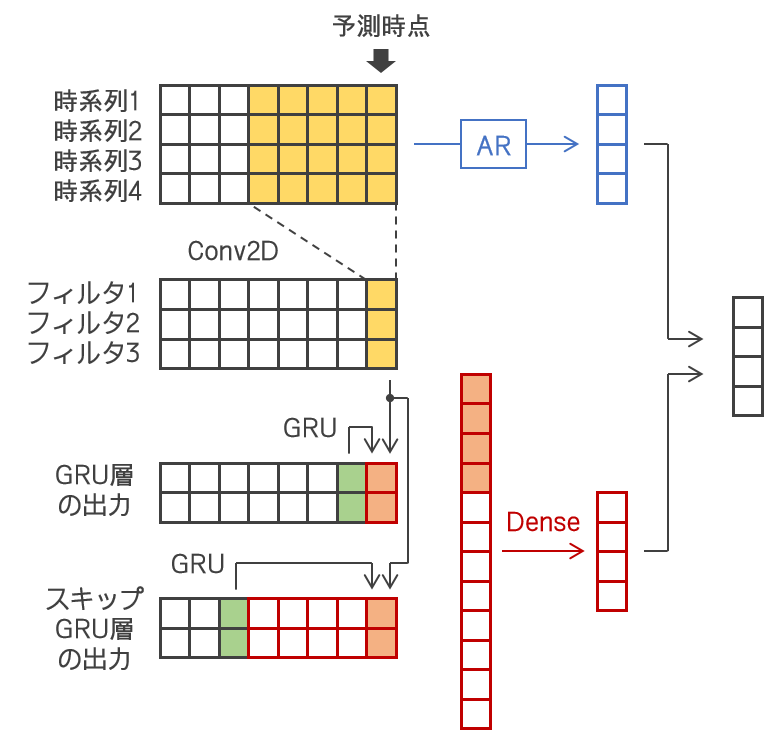
[1703.07015] Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks Long- and Short-term Time-series network (LSTNet); 2次元畳込みと再帰結合を組み合わせて、予測時に複数時系列のグローバルな情報を利用できるようにした。しかし、何千次元にはスケールしない。 https://papers.nips.cc/paper/6160-temporal-regularized-matrix-factorization-for-high-dimensional-time-series-prediction Temporal Regularized Matrix Factorization (TRMF); すべての時系列を「基底時系列」たちの線形結合で表現する。この「基底時系列」がグローバルなパターンを捉える。しかし、線形な時間依存性しか表現できない(?)。また、行列分解の際に近似誤差が生じ、個々のパターンの情報が失われやすい。