論文読みまとめ


最終更新日： 2017-02-19
参考になりそうな論文をとりあえずメモしておくページ

確率的勾配降下法

表題Shun-ichi Amari. Natural Gradient Works Efficiently in Learning, Neural Computation, Vol. 10, No. 2, pp. 251-276 (1998).
リンクhttp://www.maths.tcd.ie/~mnl/store/Amari1998a.pdf
備考自然勾配の原論文。
表題Diederik Kingma and Jimmy Ba: Adam: A Method for Stochastic Optimization, arXiv:1412.6980 (2014).
リンクhttps://arxiv.org/pdf/1412.6980v8.pdf
備考Adam の原論文。

深層学習（基礎）

表題George Cybenko: Approximation by Superpositions of a Sigmoidal Function (1989).
リンクhttp://www.dartmouth.edu/~gvc/Cybenko_MCSS.pdf
備考ニューラルネットワークの普遍性定理（Universal Approximation Theorem）の原論文。

強化学習（基礎）

表題R. J. Williams: Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning, Machine Learning, Vol. 8, Issue 3, pp. 229-256 (1992).
リンクhttp://www-anw.cs.umass.edu/~barto/courses/cs687/williams92simple.pdf
備考方策勾配のREINFORCEアルゴリズム。
表題R. S. Sutton, D. A. McAllester, S. P. Singh, and Y. Mansour. Policy Gradient Methods for Reinforcement Learning with Function Approximation, Advances in Neural Information Processing Systems 12, pp. 1057-1063 (2000).
リンクhttps://webdocs.cs.ualberta.ca/~sutton/papers/SMSM-NIPS99.pdf
備考方策のパラメータ勾配の表式、アクター・クリティックのパラメータ更新式など。
表題Peter Auer, Nicolo Cesa-Bianchi, and Paul Fischer. Finite-time Analysis of the
Multiarmed Bandit Problem. Machine Leraning, 47(2/3):235-256 (2002).
リンクhttps://homes.di.unimi.it/~cesabian/Pubblicazioni/ml-02.pdf
備考UCBアルゴリズムの原論文。
\varepsilon-greedy 方策において \varepsilon を減衰させたときのリグレットも。
表題Sebastien Bubeck and Nicolo Cesa-Bianchi. Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems. (2012)
リンクhttps://arxiv.org/pdf/1204.5721.pdf
備考様々な問題設定の多腕バンディットタスクについてリグレットを解析したサーベイ。

強化学習（応用）

表題David Silver et al., Mastering the Game of Go with Deep Neural Networks and Tree Search (2016)
リンクhttp://airesearch.com/wp-content/uploads/2016/01/deepmind-mastering-go.pdf
備考AlphaGo。
メモ雑記： AlphaGoって何 - クッキーの日記
表題Barret Zoph, Quoc Le, Neural Architecture Search with Reinforcement Learning (2016)
リンクhttps://openreview.net/forum?id=r1Ue8Hcxg
備考RNN をどんな風に設計するか自体を強化学習にやらせていると思う。

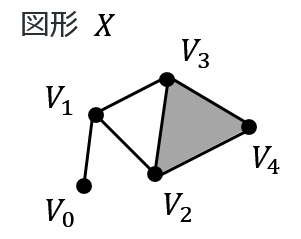
位相的データ解析（基礎）

表題Herbert Edelsbrunner, David Letscher, and Afra Zomorodian. Topological persistence and simplification（2002）
リンクhttps://www.cs.duke.edu/~edels/Papers/2002-J-04-TopologicalPersistence.pdf
備考パーシステントホモロジーの原論文。
表題Robert Ghrist, Barcodes: The Persistent Topology of Data（2008）
リンクhttps://www.math.upenn.edu/~ghrist/preprints/barcodes.pdf]
備考バーコード（＝データ点群から位相情報を抽出したフォーマットの1つ）。

「これからの強化学習」勉強会#1

本読み 強化学習

読んでいる本（出典）： これからの強化学習 | 牧野 貴樹, 澁谷 長史, 白川 真一 |本 | 通販 | Amazon

前回：ノート1 ／ 次回： 勉強会#2
目次： これからの強化学習 ／ Sutton & Barto 強化学習（邦訳）の目次： 強化学習

「これからの強化学習」の1人勉強会を開催しました。今日は初回なのでノート1で読んだ範囲の復習でした。


以下、スライドの補足でもない感想。

  • スライドの話は全然テキストに沿っていないです。スライド10頁の例がテキストに載っているわけないです。
    他のスライドも多々 Sutton 本ノートからのリサイクルです。
  • 「これからの強化学習」とSutton 強化学習とで Bellman（最適）方程式、Sarsa の位置付けが違います。
    • 価値関数導入以降の話の流れが両者で以下のような感じです。
      • Sutton： Bellman方程式 → Bellman最適方程式 → 解析解 → DP → モンテカルロ → Sarsa → Q学習
      • "これから"： モンテカルロ → Bellman方程式 → Sarsa → Bellman最適方程式 → DP → Q学習
    • つまり、Sutton では「強化学習問題をまずは理想的な状況で解析的に解こう」という流れで Bellman（最適）方程式が登場しますが、"これから" では「強化学習問題を解くだけならモンテカルロ法でごり押せるんだけど、もっと効率的に価値を推定したい」という流れで初めて Bellman 方程式が出てきます。"これから" では解析的に解こうという話自体がないようです。
    • その後の実用的な解法の紹介の順序も両者特徴的で、Sutton では「理想的な状況下で適用できるDP → 理想的でなくても適用できるモンテカルロ法／TD学習」というのに対して、"これから" では「モンテカルロ法より効率的な Sarsa → さらに効率的に、方策を陽に使用しないDP／Q学習」という感じです。
    • なので、Sutton では Sarsa は DP とモンテカルロの融合として出てきますが、"これから" では、Bellman方程式の数値解法のような感じで出てきます。これは結構違うと思います。
    • まとめると、物事には色々なストーリーのつくり方があって面白いですね。
    • そして上のスライドは Sutton 寄りです。こちらの本から読んだのでどうしても。
  • Sutton でよくわからなかった適格度トレースは、「Sutton を参照」だそうです…orz

今度こそ1.4節以降へつづく。

確率論セミナー(51)： 不参加メモ

確率論 勉強会

Skype数学勉強会 確率論セミナー に参加できなかったメモ
読んでいる本（現在はサブテキスト）： はじめての確率論 測度から確率へ : 佐藤 坦 : 本 : Amazon

参加できなかった12月22日分で発表予定だった内容のノートです。
テキスト上「明らか」の部分を補って書きました。
はてなブログへの埋め込みを SlideShare でごり押したんだけど下のページ送りボタン意味ないなと思いました。

数理論理学： ノート1

本読み 数理論理学

この本を読みます。

数理論理学数理論理学
戸次 大介

東京大学出版会 2012-03
売り上げランキング : 498190

Amazonで詳しく見る by G-Tools

次回： ノート2
目次： 数理論理学

以下、第2章の自分の理解（第1章は予備知識なので省略）。

例題　　実数 \alpha に収束する実数列 \{ a_n \, | \, n \in \mathbb{N} \} について，任意の n で a_n < A ならば， \alpha \leqq A である．
証明(1)　 \alpha > A であると仮定する．
(2)　 \alpha - A = \varepsilon_0 とおく．
(3)　(1) と (2) より， \varepsilon_0 > 0 である．
(4)　 \displaystyle \lim_{n \to \infty} a_n = \alpha より， \varepsilon_0 > 0 に対してある N_0 が存在して，任意の n > N_0 で | a_n - \alpha | < \varepsilon_0
　　である．
(5)　(4) より，任意の n > N_0 で \alpha - \varepsilon_0 < a_n < \alpha + \varepsilon_0 である．
(6)　(2) と (5) より，任意の n > N_0 で A < a_n < \alpha + \varepsilon_0 である．
(7)　(6) は 任意の n で a_n < A であることに矛盾する．
(8)　(1) と (7) より， \alpha > A ではない．
(9)　(8) より， \alpha \leqq A である．

  • でもこのようにして証明した定理はどのように "妥当" なのだろうか。物理や化学や生物学、社会学だったら、見出した定理がどのように妥当かは、現実世界の現象をどれくらいよく説明するかということになる。というかそれらの学問の目的が現実世界の現象をよく説明することである。でも数学はそういうんじゃない。
    • このくだりの教科書での表現はこのようなものではなく、「特定の力学の理論が『正しい』ということを証明することはできない」（理論にしたがわない現象が観測されれば反証されてしまうから）（14ページ）。でも数学は特別だと。
  • 数学的な訓練を受けたもの同士では（14ページ）、ある程度「この証明は妥当っぽい」とわかり合えるけど、そういう曖昧な感じでは駄目なので、「妥当な証明とは何か」をちゃんと考えることにする。それを考える学問が論理学になる。
  • 「妥当な証明とは何か」はまず「証明とは何か」から考える。上の例をみると、証明とは、文章を順番に並べたものであって、個々の文章は「 \varphi である」「 \varphi ではない」「 \varphi より， \psi である」のような形式をしている。
    • \varphi や \psi の位置にくるものは、真偽を問うことのできる形式（≡ 命題）といえる。実際、以下の (b)，(c) のような形式は証明につかわない（但し、厳密には「真偽が問えるとは何か」は論理体系による）。なお、命題に「である」「ではない」を付けたり、命題どうしを「かつ」「または」で結んだりしたものもまた真偽を問える命題になる。
      (a)　3は偶数である　\cdots 真偽が問えるので、命題
      (b)　3は偶数だと思う　\cdots 真偽が問えないので、命題ではない
      (c)　ペンパイナッポーアッポーペン　\cdots 真偽が問えないので、命題ではない
    • また、証明は命題の順不同な羅列ではなく、「 \varphi_1, \cdots, \varphi_n より， \psi である」のように命題（たち）から命題を導いていく。この形式を推論とよび、「 \varphi_1, \cdots, \varphi_n \Rightarrow \psi」とかく。また、この推論（たち）から推論を導くこともある。例えば、以下のような3ステップの証明が考えられる。
      (1)　 \varphi_1 \Rightarrow \varphi_2　\cdots 命題から命題を導出＝推論
      (2)　 \varphi_2 \Rightarrow \varphi_3　\cdots 命題から命題を導出＝推論
      (3)　(1) と (2) より， \varphi_1 \Rightarrow \varphi_3　\cdots 推論たちから推論を導出
      この証明が妥当であるには、(1)，(2) の推論が妥当な推論であり、(3) の「推論たちからの推論の導出」も妥当なものでなければならない（このうち後者のような手法の妥当性については、「妥当な推論とは何か」を決めた後で別に取り扱う）。「妥当な推論とは何か」については、この本では「意味論的推論」に基づき、「『前提の命題がすべて真であって、帰結の命題が偽である状況』が存在しない」ときにその推論を妥当とすることにする。
      (a)　すべて真である命題たち \Rightarrow 真である命題　　　\cdots 妥当な推論
      (b)　すべて真である命題たち \Rightarrow 偽である命題　　　\cdots 妥当ではない推論
      (c)　偽であるものを含むすべて真ではない命題たち \Rightarrow 真である命題　\cdots 妥当な推論
      (d)　偽であるものを含むすべて真ではない命題たち \Rightarrow 偽である命題　\cdots 妥当な推論
      恒偽式を含まなくても命題どうしが矛盾することがあるという意味で訂正（ 2017-01-07 ）
  • こうしてみると、「妥当な証明とは何か」は、以下を決めれば決まる。
    1.　推論とは何か → つまり、命題とは何か（ 推論とは「命題たち \Rightarrow 命題」なので ）
    2.　妥当な推論とは何か → つまり、命題のうち真（偽）であるものとは何か
    このうち、形式を定める 1. を統語論（syntax）といい、定めた形式の意味を決める 2. を意味論（semantics）という。この本の第Ｉ部の残りでは、「一階命題論理」と「一階述語論理」という形式体系において「妥当な証明とは何か」をどう定めるか（つまり、この「統語論」と「意味論」をどう定めるか）をみていく。

雑記： 穴を数える手続き

雑記 位相的データ解析

あなたは以下の図形 X にいくつ穴があるか求めるようお客様に要求されたとします。
灰色の部分は面で埋まっているとします。

f:id:cookie-box:20161204111813p:plain:w160
あなたはこう答えたいです。
　f:id:cookie-box:20161204115026p:plain:w130
だっても何も、図形 X の穴は V_1 V_2 V_3 がなす三角形の1個だからです。
しかし、これではお客様へ要件定義の説明責任を果たせません。というか要件定義していません。
あなたの出した結論が、バグがない、品質のよいものなのかどうか全くわかりません。
また、より複雑な図形になったとき、同じようには対応できないかもしれません。
そこで、再現可能な手続きでもって求め直したいと思います（以下）。

f:id:cookie-box:20161204110733p:plain:w460

  • まず頂点と辺と面を列挙してください。
  • チェイン複体を構成してください。C_0(X) は各頂点に係数を掛けて足したもののなす空間だと思ってください。図形 X には頂点が5つあるので \mathbb{R}^5 になります。ここで、簡単のため & 今回の目的を満たすのに十分なため、係数のとりうる値は \mathbb{R} としました。場合によっては \mathbb{Z} とか \{ 0, 1\} かもしれないので気を付けてください。
    境界作用素 \partial _1 , \; \partial _2 は、「辺の係数空間から頂点の係数空間への写像（ \mathbb{R}^6 から \mathbb{R}^5 への写像）」「面の係数空間から辺の係数空間への写像（ \mathbb{R} から \mathbb{R}^6 への写像）」とでもいうべき写像ですが、ここでは上のように行列表示できるものと定義します。なぜこうしたのかは、何となくわかるかもしれませんが、 \partial _1 の1列目が「辺 V_0 V_1 は頂点 V_0 と頂点 V_1 を境界としてもつ」に対応しています。これはチェイン複体の境界作用素への要請 \partial _n \circ \partial _{n+1} = 0 を満たします。
    ここで便宜上、写像 \partial _1 , \; \partial _2 を行列であるかのように書いています。
  • あとは1次ホモロジー群 H_1(X) の次元を求めてください。線形代数の基礎知識によります。
    • 剰余群をとる操作は、集合「 Z_1 (X) ＝ 図形 X に含まれる全ての（係数の重み付き）閉じたループ（辺のセット）」の元の中で、集合「 B_1 (X) ＝ 図形 X に含まれる（係数の重み付き）閉じたループであって面で埋まっているもの」の元の差しかないものを同一視することに相当します。H_1(X) の元を数えるとは、全ての閉じた（係数の重み付き）ループをカウントするが、中が面で埋まったループがくっついているかどうかの違いしかない場合は重複してカウントしない、ということになります。H_1(X) の元の数をそのまま見てしまうと各辺に係数の重みを課す分無数にあるので、穴の数をとるには係数空間の次元を取ります。
    • 同様に、{\rm dim}\bigl(H_0(X)\bigr)=1 で連結成分の数、{\rm dim}\bigl(H_2(X)\bigr)=0 で空洞の数も求まる。というより、「図形 X の連結成分の数」「図形 X の穴の数」「図形 X の空洞の数」をこの量で定義した、といった方が正しい。

参考文献