深層学習には Keras が便利という巷の評判に流されて Keras を勉強します。
でも冷静に考えると普段から別に深層学習などやっていなかったので、そういうのは今後やります。
参考文献
以下の記事を全面的に参考にさせていただきました。
aidiary.hatenablog.com
使用データ
手元にある都合上、以下の2章に出てくる10000人の身長・体重データをつかいます。データは GitHub にあります。
 | 入門 機械学習 Drew Conway John Myles White 萩原 正人 オライリージャパン 2012-12-22 売り上げランキング : 243617 Amazonで詳しく見る by G-Tools |
上のデータをプロットすると以下のようになります。たぶんアメリカ人のデータです。データ上、前半5000レコードが男性、後半5000レコードが女性なので女性の点が上に重なってみえます。
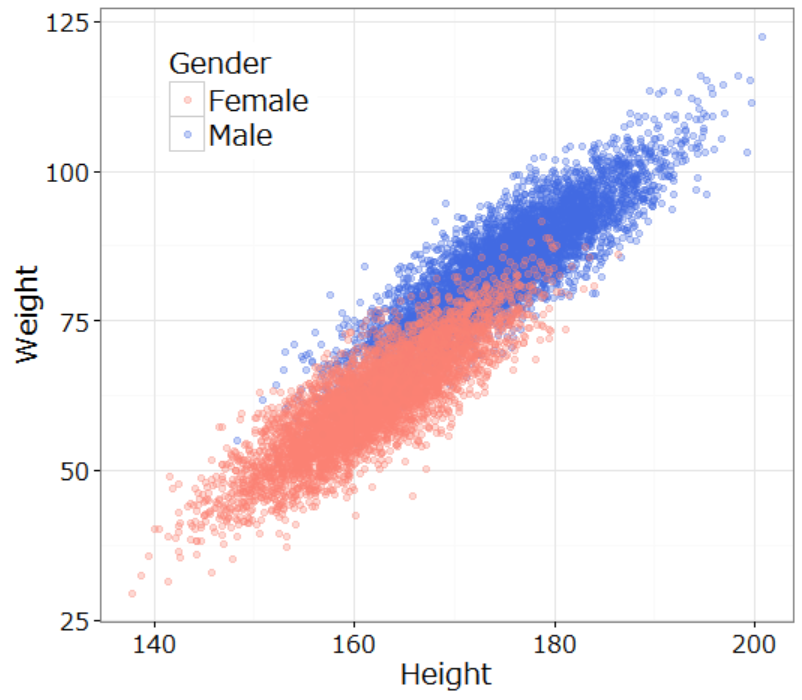
やること
上図の Height‐Weight 平面に直線を引いて男女を分離できるかというと完全にはできないですが、だいたい合っていればいいと思えばできるので、一番いい直線をロジスティック回帰で求めます。
要は、以下のピンク色の係数の最適化をします。

手順
データを R でもっていることが多い都合上、無駄に R を経由します。
まず R でデータを読み込んでダミー変数を付与します。ヤードポンド法も撲滅します。なお、結局正規化するので特に撲滅する意味はないです。
data.file <- file.path('data', '01_heights_weights_genders.csv') heights.weights <- read.csv(data.file, header=TRUE, sep = ',') heights.weights$Height <- 2.54 * heights.weights$Height # インチ --> センチ heights.weights$Weight <- 0.45359237 * heights.weights$Weight # ポンド --> キログラム heights.weights$Male <- ifelse(heights.weights$Gender=='Male', 1, 0) # 男性なら1、女性なら0 save(heights.weights, file='heights_weights_genders.RData')
Gender Height Weight Male 1 Male 187.5714 109.72107 1 2 Male 174.7060 73.62279 1 3 Male 188.2397 96.49763 1
次に Python から読みこんで Keras にロジスティック回帰してもらいます。ほとんど参考記事通りのコードです。
参考記事の記述通り、データは正規化しないと全くトレーニングが進みませんでした。初期値を何とかすればいいのかもしれませんが。
# -*- coding: utf-8 -*- from sklearn import preprocessing from keras.models import Sequential from keras.layers.core import Dense, Activation import pyper import pandas import numpy if __name__ == "__main__": # load data r = pyper.R(use_pandas='True') r("load(\"heights_weights_genders.RData\")") heights_weights = pandas.DataFrame(r.get("heights.weights")) heights_weights.columns = ['Gender', 'Height', 'Weight', 'Male'] x = numpy.array(heights_weights.ix[:,('Height', 'Weight')]) y = numpy.array(heights_weights.ix[:,'Male']) r = None # normalize data x = preprocessing.scale(x) r = pyper.R(use_pandas='True') r.assign("heights.weights.mod", x) r("save(heights.weights.mod, file=\"heights_weights_mod.RData\")") r = None # create model model = Sequential() model.add(Dense(1, input_shape=(2, ))) model.add(Activation('sigmoid')) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) # train model model.fit(x, y, nb_epoch=1000, batch_size=100, verbose=1) # result result = model.layers[0].get_weights() w1 = result[0][0, 0] w2 = result[0][1, 0] b = result[1][0] print w1, w2, b
Epoch 1/1000 10000/10000 [==============================] - 0s - loss: 0.7057 - acc: 0.5044 Epoch 2/1000 10000/10000 [==============================] - 0s - loss: 0.6449 - acc: 0.6339 Epoch 3/1000 10000/10000 [==============================] - 0s - loss: 0.5955 - acc: 0.7099 ... Epoch 999/1000 10000/10000 [==============================] - 0s - loss: 0.2091 - acc: 0.9194 Epoch 1000/1000 10000/10000 [==============================] - 0s - loss: 0.2091 - acc: 0.9193 -1.89395 6.36942 0.0175593
上の実行結果では、最終的な正解率が 0.9194 とか 0.9193 になっていますが、そもそも上図のデータを直線で分離しようというのが雑な話なのでこれよりよくならないです。なお、R の glm でロジスティック回帰しても正解率は 0.9194 になります(以下;但し、シグモイド関数の出力が 0.5 未満を女性判定、0.5以上を男性判定とします)。
性別を正しく判定できなかった 806人の方には申し訳ありませんが、致し方ないです。
logit.model <- glm(Male ~ Weight + Height, data = heights.weights, family = binomial(link = 'logit'))
> logit.model
Coefficients:
(Intercept) Weight Height
0.6925 0.4373 -0.1939
> length(which(floor(logit.model$fitted.values + 0.5) == heights.weights$Male))
[1] 9194
左が Keras の結果(但し、平均0、標準偏差1になるよう正規化済み)、右が R glm の結果です。

