参考文献: Amazon.co.jp: 強化学習: Richard S.Sutton, Andrew G.Barto, 三上 貞芳, 皆川 雅章: 本
この記事は上の本の37ページのグラフの再現です。
こちらの記事のグラフに L_R-I と L_R-P を足したもの。
- ゲーム設定
- 2つのスロットマシンAとBがあって、アームを引いたら確率的にコインが出るか出ないのどちらか。
- 設定その1ではどちらのマシンでもコインが出る確率が低く(10%, 20%)、設定その2ではどちらでも高い(80%, 90%)。いずれにせよBを選ぶのが最適(だが、それは外からすぐにはわからないだろう)。
- 500回アームを引くうちに何らかの判断をしていってなるべくよい方のマシンをたくさん引きたい。
- 戦略
- 赤色 教師あり: コインが出たらそのマシンを、出なかったら他方のマシンを正解と考える。
- 黄色 教師あり(L_R-P): 赤色と同じ正解の推定をするが、選択確率は徐々に調整する。
- 緑色 教師あり(L_R-I): 黄色とほぼ同じだが、実際にコインが出たときのみ選択確率を更新する。
- 青色 εグリーディ: 正解があることは前提にせず、これまでの結果からより期待できるマシンを推定する。ときどき期待値が低い方のマシンも調べる。
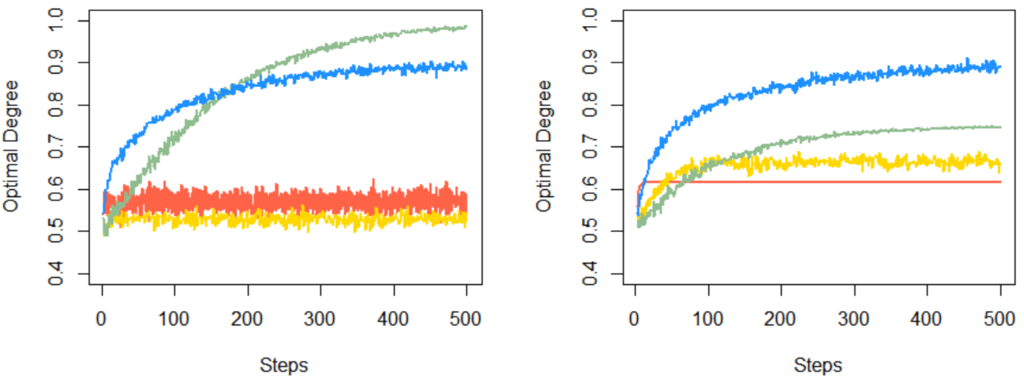
- 結果(2000回試行の平均: 左側が設定その1、右側が設定その2)
- 個人的な解説
- 赤色と黄色はいずれの設定でも他の戦略よりよくない。コインが出る確率がどっこいどっこいという問題設定に対して、「コインが出たらそのマシン、コインが出なかったら他方のマシンが正解!」という姿勢がそもそもよくないのでは。それは外からわからないんだろうけど、なら尚更そういう強い姿勢は避けるべきでは。これらの種の教師あり学習がこのゲームに有効じゃなかったというより、なんか姿勢が駄目だと思う。
- 緑色も教師あり学習だけど、コインが出たときに出た方を選びやすくする調整をするのがいくぶん教師なし学習に近い。設定その1では、コインがまだ全然出ないゲームの序盤では選択確率が更新されない分くまない探査ができ、実質的にεを漸減させるεグリーディとして機能しているはず。なので青色より強い。設定その2では、コインがじゃんじゃん出るので片方のマシンにトラップされて早期に探索できなくなっていく分、青色より弱い。と思います。
- 弱いといっても、どちらのマシンもコインがじゃんじゃん出るなら目的によってはよいのでは。
- でも世の中には正解の行動は何かという視点から考えるのが難しい問題もあるので、正解の行動に近づいていこう、という教師あり学習にはその点でやはり限界がある。
以下、上記のスクリプト。
n.draw <- 500 # アームを何回ドローするか # ベクトルのうち一番大きい値のラベルを返す補助関数 # ※ 同率1位があるときはランダムな選択にする get.best.label <- function(data.hist) { label <- names(which.max(data.hist)) data.hist <- data.hist[data.hist == data.hist[[label]]] labels <- names(data.hist) return(labels[[ceiling(runif(1) * length(labels))]]) } # 1回のタスク Task <- function( setting, # ゲーム設定データフレーム rands.for.reward, # 各ドローの報酬決定用の乱数 method, # 方針: Supervised (教示的), Evaluative (評価的), L_R-P, L_R-I rands.for.explore=rep(0.0, n.draw), # 評価的な方針でのみ使用 epsilon=0.0, # 評価的な方針でのみ使用 rands.for.select=rep(0.0, n.draw), # L_R-P, L_R-I, 評価的な方針でのみ使用 alpha=0.1 # L_R-P, L_R-I でのみ使用 ) { # i 回目に指定のラベルのアームを引いたときの報酬 Draw <- function(label, i) { return(ifelse(rands.for.reward[[i]] < setting$prob[setting$label==label], 1, 0)) } # 過去に推定した正答をためる用 (教示的な方針でのみ使用) estimation.hist <- rep(0, nrow(setting)) names(estimation.hist) <- setting$label # 各ラベルの選択確率の記録用 (L_R-P, L_R-Iでのみ使用) probs.select <- rep(1/nrow(setting), nrow(setting)) names(probs.select) <- setting$label # 過去の結果をためる用 (評価的な方針でのみ使用) rewards.hist <- list() for (label in setting$label) { rewards.hist <- c(rewards.hist, list(c())) } names(rewards.hist) <- setting$label # 作業開始 labels.all <- c() rewards.all <- c() # 最初はすべての行動を試す (仮) for (i.draw in 1:nrow(setting)) { label <- setting$label[[i.draw]] labels.all <- c(labels.all, label) reward <- Draw(label, i.draw) rewards.all <- c(rewards.all, reward) if (method == "Supervised") { # 教示的な方針のときの情報更新 label.estimate <- ifelse(reward == 1, label, setting$label[setting$label != label]) estimation.hist[[label.estimate]] <- estimation.hist[[label.estimate]] + 1 } else if (method == "L_R-P" || (method == "L_R-I" && reward == 1)) { # L_R-P, L_R-I のときの情報更新 label.estimate <- ifelse(reward == 1, label, setting$label[setting$label != label]) # 正解だと思ったラベルの選択確率をちょっと上げる prob.diff <- alpha * (1 - probs.select[[label.estimate]]) probs.select[label.estimate] <- probs.select[label.estimate] + prob.diff # その他のラベルの選択確率をちょっと下げる label.other <- setdiff(setting$label, c(label.estimate)) probs.select[label.other] <- probs.select[label.other] - prob.diff / length(probs.select[label.other]) } else if (method == "Evaluative") { # 評価的な方針のときの情報更新 rewards.hist[[label]] <- c(rewards.hist[[label]], reward) } } # その後は方針にしたがって行動 for (i.draw in (nrow(setting)+1):n.draw) { label <- NA if (method == "Supervised") { # 教示的な方針のときのラベル判断 label <- get.best.label(estimation.hist) } else if (method == "L_R-P" || method == "L_R-I") { # L_R-P, L_R-I のときのラベル判断 label <- setting$label[cumsum(probs.select) - rands.for.select[[i.draw]] > 0][[1]] } else if (method == "Evaluative") { # 評価的な方針のときのラベル判断 values <- sapply(rewards.hist, mean) label.optimum <- get.best.label(values) if (epsilon == 0) { # 利用 label <- label.optimum } else { if (rands.for.explore[[i.draw]] < epsilon) { # 探査 labels.cand <- setting$label[setting$label != label.optimum] label <- labels.cand[[ceiling(rands.for.select[[i.draw]] * length(labels.cand))]] } else { # 利用 label <- label.optimum } } } labels.all <- c(labels.all, label) reward <- Draw(label, i.draw) rewards.all <- c(rewards.all, reward) if (method == "Supervised") { # 教示的な方針のときの情報更新 label.estimate <- ifelse(reward == 1, label, setting$label[setting$label != label]) estimation.hist[[label.estimate]] <- estimation.hist[[label.estimate]] + 1 } else if (method == "L_R-P" || (method == "L_R-I" && reward == 1)) { # L_R-P, L_R-I のときの情報更新 label.estimate <- ifelse(reward == 1, label, setting$label[setting$label != label]) # 正解だと思ったラベルの選択確率をちょっと上げる prob.diff <- alpha * (1 - probs.select[[label.estimate]]) probs.select[label.estimate] <- probs.select[label.estimate] + prob.diff # その他のラベルの選択確率をちょっと下げる label.other <- setdiff(setting$label, c(label.estimate)) probs.select[label.other] <- probs.select[label.other] - prob.diff / length(probs.select[label.other]) } else if (method == "Evaluative") { # 評価的な方針のときの情報更新 rewards.hist[[label]] <- c(rewards.hist[[label]], reward) } } return(list(labels.all, rewards.all)) } n.task <- 2000 # タスクを何セット試行するか par(mfrow=c(1,2)) settings <- list( # ゲーム設定その1 (36ページの図2.2のA) data.frame( label=c("A", "B"), prob=c(0.1, 0.2), stringsAsFactors=FALSE ), # ゲーム設定その2 (36ページの図2.2のB) data.frame( label=c("A", "B"), prob=c(0.8, 0.9), stringsAsFactors=FALSE ) ) for (i.setting in 1:length(settings)) { # 行動の最適度を記録 optimal.degree.supervised <- rep(0.0, n.draw) optimal.degree.L_R.P <- rep(0.0, n.draw) optimal.degree.L_R.I <- rep(0.0, n.draw) optimal.degree.evaluative <- rep(0.0, n.draw) for (i.task in 1:n.task) { # タスクを繰り返し行動の最適度を足し上げていく rands.for.reward <- runif(n.draw) rands.for.explore <- runif(n.draw) rands.for.select <- runif(n.draw) result <- Task(settings[[i.setting]], rands.for.reward, "Supervised") optimal.degree.supervised <- optimal.degree.supervised + ifelse(result[[1]]=="B", 1, 0) result <- Task(settings[[i.setting]], rands.for.reward, "L_R-P", rands.for.select=rands.for.select, alpha=0.1) optimal.degree.L_R.P <- optimal.degree.L_R.P + ifelse(result[[1]]=="B", 1, 0) result <- Task(settings[[i.setting]], rands.for.reward, "L_R-I", rands.for.select=rands.for.select, alpha=0.1) optimal.degree.L_R.I <- optimal.degree.L_R.I + ifelse(result[[1]]=="B", 1, 0) result <- Task(settings[[i.setting]], rands.for.reward, "Evaluative", rands.for.explore, 0.1, rands.for.select) optimal.degree.evaluative <- optimal.degree.evaluative + ifelse(result[[1]]=="B", 1, 0) } # 1タスクあたりの平均値に換算 optimal.degree.supervised <- optimal.degree.supervised / n.task optimal.degree.L_R.P <- optimal.degree.L_R.P / n.task optimal.degree.L_R.I <- optimal.degree.L_R.I / n.task optimal.degree.evaluative <- optimal.degree.evaluative / n.task # プロット (最初の2回は決まったラベルを選択しているのでトリム) plot(c(3, n.draw), c(0.4, 1.0), xlab="Steps", ylab="Optimal Degree", type="n") lines(3:n.draw, optimal.degree.supervised[3:n.draw], col="tomato", lwd=2) lines(3:n.draw, optimal.degree.L_R.P[3:n.draw], col="gold", lwd=2) lines(3:n.draw, optimal.degree.L_R.I[3:n.draw], col="darkseagreen", lwd=2) lines(3:n.draw, optimal.degree.evaluative[3:n.draw], col="dodgerblue", lwd=2) }