例えば MoviePy パッケージには Sphinx によるドキュメントが用意されています。
User Guide — MoviePy 1.0.2 documentation
そうすると自分のパッケージにもそのようなドキュメントを用意したくなると思います。なので、MoviePy 同様に Sphinx ツールを利用し、ホスティングサービスに Read the Docs を利用します。参考文献 1. の Sphinx-RTD チュートリアルにしたがいます。そうするとなんやかんやで以下のようなドキュメントができます。
Welcome to cookies_utilities’ documentation! — cookies_utilities 0.0.4 documentation
なお、この記事に対応するファイル一式はこちらですが、ドキュメント追加前との差分は以下の色が付いたディレクトリ・ファイルです（水色は新規作成、緑色は自動生成、ピンク色は自動生成したものを編集、オレンジ色は既存ファイルを編集）。
cookies_utilities/
├── .readthedocs.yaml # 新規作成する
├── docs/ # 新規作成して直下で sphinx-quickstart コマンドを叩くと以下のファイルが自動生成する
│ ├── make.bat
│ ├── Makefile
│ ├── build/
│ └── source/
│ ├── conf.py # html_theme = 'sphinx_rtd_theme' に変更し autodoc の設定をする
│ ├── index.rst # ドキュメントのトップページなので適宜編集する
│ └── cookies_utilities.rst # sphinx-apidoc コマンドで生成されるので適宜編集する
├── pyproject.toml # 適宜 Python バージョンを RTD に対応させる、適宜 RTD へのリンクを追加する
├── LICENSE
├── README.md
├── src/
│ └── cookies_utilities/
│ ├── __init__.py
│ └── stopwatch.py # 適宜 Docstrings をかく
└── tests/
└── test_stopwatch.py
参考文献 1. にしたがい以下をインストールします。
pip install sphinx
pip install sphinx-rtd-theme
参考文献 1. では simpleble なるパッケージをチュートリアルの題材にしており、このパッケージが参照する bluepy のインストールも要求していますが、このパッケージは Windows に対応していないので入れないですというか入れられないです。ただ自作パッケージの依存パッケージも sphinx と同じバージョンの pip で入れるように注意があるので将来に機会があればそれにしたがいます。今回の自分のパッケージは依存パッケージがないので対応することはないです。
自分のパッケージの
リポジトリをクローンして docs
ディレクトリをつくります。
cookies_utilities/
├── docs/ <-- New!
├── pyproject.toml
├── LICENSE
├── README.md
├── src/
│ └── cookies_utilities/
│ ├── __init__.py
│ └── stopwatch.py
└── tests/
└── test_stopwatch.py
つくった docs ディレクトリに移動して sphinx-quickstart コマンドを実行します。色々質問されるので以下のように答えます（チュートリアルではもっと色々質問が続いていたのですが私の場合はここで終わってしまいました）。
$ mkdir docs
$ cd docs
$ sphinx-quickstart
> ソースディレクトリとビルドディレクトリを分ける（y / n） [n]: y
> プロジェクト名: cookies_utilities
> 著者名（複数可）: CookieBox26
> プロジェクトのリリース []: 0.0.4
> プロジェクトの言語 [en]: en
そうすると docs 以下にファイルやディレクトリが生成されます。
cookies_utilities/
├── docs/
│ ├── make.bat
│ ├── Makefile
│ ├── build/
│ └── source/
│ ├── conf.py
│ └── index.rst
（略）
生成された source/conf.py に以下の変更をします。
- html_theme = 'sphinx_rtd_theme' にする。
- コード中のコメントからドキュメントを自動生成したいときはさらに以下の 2 点を対応する。
- extensions = ['sphinx.ext.autodoc'] とリストに加える（チュートリアルでは sphinx-quickstart 実行時にこれも質問されていたのですがなぜか私は質問してもらえなかったので手動で加えます）。
- ファイルの先頭に以下を追記する。
import os
import sys
sys.path.insert(0, os.path.abspath('../../src/cookies_utilities/'))
コードにコメントを記述する
Sphinx にドキュメントを自動生成してもらえるように
Sphinx docstring 形式でコードにコメントをかきます。
Writing docstrings — Sphinx-RTD-Tutorial documentation私は以下のようにかきました。Summary と param の間には空行が必要です（さもないとすべて Summary になってしまいます）。
class Stopwatch:
""" Stopwatch for measuring processing time.
"""
def __init__(self):
self.cache = []
def press(self, key=''):
""" Press the stopwatch.
:param key: The idenficator for the time, defaults to ''
:type key: string, optional
"""
self.cache.append((key, time.perf_counter()))
reStructuredText ファイルを整備して HTML ファイルにビルドする
ドキュメントはまず reStructuredText ファイル（.rst ファイル）一式として用意して、その後に HTML ファイル一式にビルドすることになります。まず、さっきコメントをかいたのをドキュメントにしたいので docs 以下で以下を実行して ./source/modules.rst, ./source/cookies_utilities.rst を生成させます。
sphinx-apidoc -o ./source ../src/cookies_utilities
このうち ./source/modules.rst はチュートリアルにあるようにモジュールがたくさんあるとき便利なようですが、今回の自分のパッケージには stopwatch.py しかないので無視します。./source/cookies_utilities.rst の方も cookies_utilities.Stopwatch の説明さえあればいいのでチュートリアルを参考にかなり編集してしまいます。
Documentation
=============
The ``cookies_utilities.Stopwatch`` class
*****************************************
.. autoclass:: cookies_utilities.Stopwatch
:members:
:undoc-members:
:show-inheritance:
./source/index.rst からリンクを張らないと意味がないのでこちらのファイルも編集します。自動生成された状態では cookies_utilities's となってしまっているので最後の s を取るなどの手直しもします。
Welcome to cookies_utilities' documentation!
=============================================
.. toctree::
:maxdepth: 2
:caption: Contents:
cookies_utilities.rst
Indices and tables
==================
* :ref:`genindex`
* :ref:`search`
.rst ファイルの手直しができたら docs 以下で以下を実行して HTML ファイル一式をビルドします。
./make.bat clean # Windows でない人は make clean
./make.bat html # Windows でない人は make html
ここで ERROR: Unknown directive type "autoclass" といわれるようなら conf.py において extensions = ['sphinx.ext.autodoc'] としてあるか確認します（参考文献 2.）。また、No module named 'cookies_utilities' といわれて自分のパッケージを認識してくれないようなら一階層上に戻って手動でインストールしてしまいます。setup.py 式でないので自動でインストールしてくれないのかよくわかりません。
cd ..
pip install -e .
cd docs
./make.bat clean
./make.bat html
そうすると docs/build/html/index.html に素敵なページが作成されます。コードコメントが自動でドキュメント化されているのもわかります。自分のパッケージ内のクラスやメソッドの Index も生成されています。
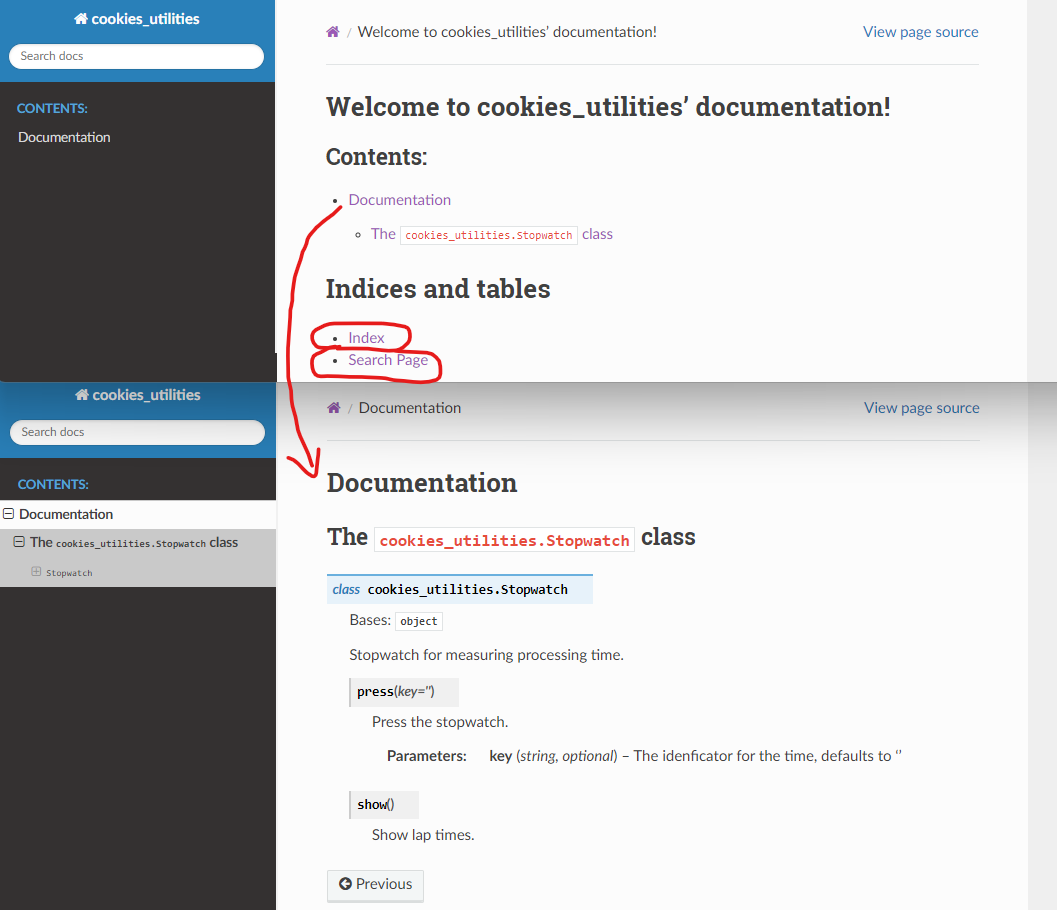
Search Page はローカルでは機能しませんが問題ありません → と思いましたが後にパブリッシュしても機能していませんでした。何ならチュートリアルの Search Page も機能しておらずこれはバグのようです（参考文献 3.）。なので私はリンクを消しました。
GitHub リポジトリに push し Read the Docs にパブリッシュする（要 .readthedocs.yaml ）
以下のファイルを
GitHub リポジトリに push します。
docs/make.bat
docs/Makefile
docs/source/conf.py
docs/source/cookies_utilities.rst
docs/source/index.rst
docs/source/modules.rst
src/cookies_utilities/stopwatch.py
そうしたらリポジトリを Read the Docs から参照します。まずは Read the Docs にアカウント登録します。GitHub アカウントと連携すると自分のリポジトリ一覧が Read the Docs からみられるので cookies_utilities を選択します。ただ選択しようとすると「リポジトリ直下に .readthedocs.yaml はありますか」と確認されると思います。まだ用意していないので巷の同名のファイルを調べつつ以下のように用意します。
version: 2
sphinx:
configuration: docs/source/conf.py
python:
version: 3.8
install:
- method: pip
path: .
python.version を 3.8 としているのは当初 3.10 にしたところ、Read the Docs 上で 3.8 までで選べとエラーになったからです。なお、
.readthedocs.yaml 上で
python.version を下げると
pyproject.toml の
project.requires-python も連動して下げなければやはりエラーになります。
[project]
requires-python = ">=3.8"
今回の自分のパッケージは実際
Python 3.8 でもいいのでバージョンを下げましたが、本当に
Python のもっと大きいバージョンを要求するパッケージのときはどうするといいのかわかっていません。そんなわだ
かまりはありますがともあれ自分のパッケージのドキュメントが以下のようにパブリッシュされます。
Welcome to cookies_utilities’ documentation! — cookies_utilities 0.0.4 documentation
だったら、
を以下のようにとる。
