カーネル法入門：ノート1 - クッキーの日記

以下の本を読みます。キャラクターは架空のものです。解釈の誤りは筆者に帰属します。お気付きの点がありましたらコメント等でご指摘いただけますと幸いです。

カーネル法入門―正定値カーネルによるデータ解析 (シリーズ多変量データの統計科学)

作者:健次, 福水
朝倉書店

以前カーネル法を勉強したときの記事：パターン認識と機械学習下（第6章：その6〈終〉） - クッキーの日記

次回：まだ

f:id:cookie-box:20190101155733p:plain:w60

まえがきから読み始めると冒頭からカーネル法とは何かきっぱり書いてありますね。つまり、「正定値カーネルの定める再生核ヒルベルト空間を用いたデータ解析の方法論」とのことです。…データ解析に「空間を用いる」とは何でしょう？「ほにゃららモデルを用いる」、ならわかるんですが…まえがきの続きによるとこの再生核ヒルベルト空間とは関数空間であるらしいですが、何が何やら…まあ置いておきましょう。冒頭にはカーネル法とは「データの非線形性や高次モーメントを扱うための方法論」ともありますね。データの非線形性や高次モーメントを扱うとは？

f:id:cookie-box:20190101160814p:plain:w60

おそらく1章の2～3ページで挙げられているのが最も簡単な例だね。「データの線形性しか扱わない」というのは、「データの空間のどこかにデータを仕切るような超平面を置いて、その超平面から表側に垂直に離れるほどプラスのスコア、裏側に垂直に離れるほどマイナスのスコア、のようなスコア付けでもってデータを分類したり回帰したりしようとする」ということだろう。でもまっすぐな仕切りで仕切れないのが図1.1の例だね。「高次モーメントを扱う」というのは「2つの変数 $X, \, Y$ に対して $X$ の $n$ 次かつ $Y$ の $m$ 次のモーメントからわかる依存関係を捉える」って感じなんだろうか。図1.2は $X$ の方を2乗しないと相関係数が小さくなる例だね。相関係数がゼロであることは独立であることを意味しないというのは有名だね（ウィキペディアの「相関係数」の頁の絵）。

相関係数 - Wikipedia

そこまでごり押されなくても「線形の解析では不十分」であることに異存はないですよ…。確かに、図1.1で分類しようとしたり、図1.2で $X$ がどうなると $Y$ がどうなるかという関係を見出したりするには線形関数では足りませんね…もっと柔軟なモデルでなければ…解決策を思い付きました。決定木を使いましょう。

解決できるのはできると思うけど、本のタイトルが「決定木入門」になっちゃうかな。

図1.1の方は図の2次元空間の上に $f(x_1, x_2)$ という「その場所では＋か ○ のどちらか」という関数を見つけたいのですよね。それを $f(x_1, x_2) = \hat{f}(\phi(x_1, x_2)) = \hat{f}(z_1, z_2, z_3)$ とすることで $\hat{f}$ を線形関数で足りるようにしたんですね。図1.2の方は、 $f_1(x)$ と $f_2(y)$ の相関を最大化するのに、 $f_1(x) = \hat{f_1}(\phi(x)) = \hat{f_1}(x^2)$ とすることで $\hat{f_1}$ を線形関数で足りるようにしたという感じでしょうか。…なんというか、これらをみるとカーネル法とはむしろ「何が何でも線形関数で解く。線形関数で解けるようにデータの方が動くべき」というものにみえますね。ニューラルネットワークの方が人としての器が大きいのではないですか？あちらは「データはそのままでどんな関数でも表現する」でしょう？

人じゃないからね。カーネル法はカーネル法で（あるクラスの最適化問題に対する正定値カーネルの定める再生核ヒルベルト空間内での）最適解が線形関数の形でかけるという理論的裏付けと、さまざまな拡張があるんだよ。「線形関数で解けるようにデータの方が動くべき」というようにデータの方が一旦動いてくれたら、その上に線形な依存性に基づいたさまざまな分析手法を応用することができるんだから。

はあ。まあ何にせよカーネル法ではデータを都合よく動かさなければならないということですよね。しかし4ページをみると、あらゆる高次のモーメントを考慮するには組合せが爆発してしまうようですが。前途多難では？

にもかかわらず効率的に高次モーメントを抽出できますよというのがカーネル法の売りだからね。

どうやってそんなことを…まあそれがこれからの話題ですか。1.1.2節に移りましょう。データの空間が $\Omega$ で、それを移す実ベクトル空間が $H$ ですか。図1.1や図1.2の左側が $\Omega$ 、右側が $H$ ということですよね？ …実ベクトル空間というのは？

集合であって、和やスカラー倍が入ってて、和やスカラー倍が結合律やら分配律やらを満たすやつ。「実」ベクトル空間といったときはスカラーは $\mathbb{R}$ の元だね。

それは結局、ベクトルを集めた集合ではないんですか？ 3次元実数ベクトルが入っている $H$ は結局 $\mathbb{R}^3$ ということではないんですか？

どちらかというと実ベクトル空間の条件を満たす集合があったとき、その元をベクトルというかな。あと、3次元実数ベクトルを含む $H$ でも、 $\mathbb{R}^3$ 内のある平面だけとかある直線だけとかの実ベクトル空間はありうるね。

あー平面や直線の中で和やスカラー倍はできますね…まあ、データを和やスカラー倍がちゃんとできる空間にもってくるのだと理解しました。そうですね、元のデータが単語や文章などであったら、和やスカラー倍をしようとしても和やスカラー倍とは何か定かではありませんね。あれでも、 $H$ は内積ももたなければならないと続きにありますね。

データ分析では点がどのように密集（分布）しているかに興味があるからね。「ここに仕切りを入れられそうだ」「これが主成分だ」とかいうには点どうしの近さが決まっていないと始まらない。

それって決めないと決まらないものですか？内積って $x_1 y_1 + x_2 y_2 + x_3 y_3$ のように授業で習った気がするのですけど。

それは実数ベクトルの標準内積だね。それに決めてもいいよ。でもそれとは違う内積に決めてもいい。例えば、 $100 x_1 y_1 + x_2 y_2 + x_3 y_3$ みたいに、1つ目の軸方向だけやたら重視する内積でもいいよ。そうしたかったらね。内積が満たすべき性質は、付録の193～194ページだね。

なんと、そういう内積もありなんですか？一旦193ページにとびますか。…って、内積より前にまずノルムというものが出てきますね。その後に内積はこういうものというのも出てきて…内積が定義できればその $1/2$ 乗をノルムにできるってことですね。なるほど、副部長がいう定義も内積の性質を満たしますね。

対称行列 $A$ について、 $x^{\top}Ay$ は内積になるからね。

まあ何にせよ何かしら内積を決めたとして、でも $H$ が高次元だと内積計算にはコストがかかると…それはそうかもしれませんが。でもカーネル法ではその内積計算がカーネル関数 $k$ の評価で済む？えっと、話を整理しましょう。いま、手元のデータを分析するのに、線形の依存性を調べるのでは不十分なので、高次元の依存性を調べたくて、つまり高次元の項も含めた内積を計算したくて、それにはカーネル値 $k(X_i, X_j)$ を計算すればよい。…ちょっと最後が飛躍しすぎですね。

それはおいおいかな。そこがカーネル法の基本原理だからね。5ページからは実用例みたいな話が始まってるね。

カーネル主成分分析、ですか。通常の主成分分析もわからないのですが…python の scikit-learn でも使えるようなのでまずは実行してみますか。

sklearn.decomposition.KernelPCA — scikit-learn 1.0 documentation

データはそうですね、非線形性があるものがいいのですよね。以下にスイスロールのデータがあったのでこれをお借りすることにします。3次元で、y軸に垂直に切ると渦巻きになっているようなデータですね。

a Swiss Roll Dataset

上のデータに sklearn.decomposition の PCA と KernelPCA を適用したのが下図です（スクリプトは記事の最下部）。左上が元のデータをxy平面に落とした図、右上が元のデータをxz平面に落とした図ですね。左下が通常の主成分分析の第1主成分-第2主成分、右下がカーネル主成分分析の第1主成分-第2主成分です。上段の実線は通常の主成分分析の第1主軸の方向、点線が第2主軸の方向ですね。データ点は上のリンク先の gif と同じ4色の塗分けをしています。よくみると、スイスロールはこの4つのクラスタに切り分けられるのかもしれませんね。色が同じ部分がやや密集しているようです。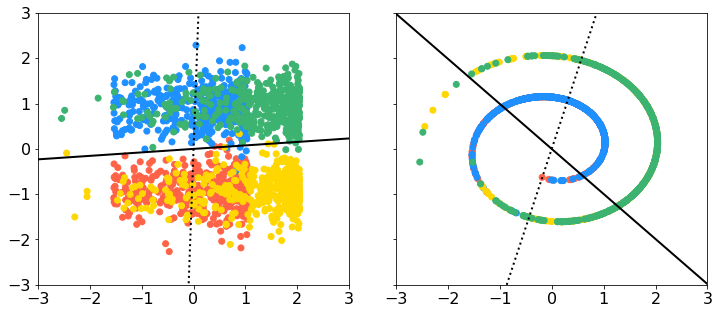
f:id:cookie-box:20190321180703p:plain:w540

f:id:cookie-box:20190321180703p:plain:w540

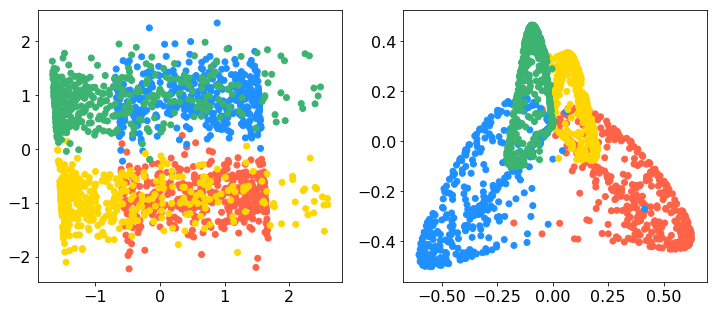
f:id:cookie-box:20190321180731p:plain:w540

…通常の主成分分析はほとんどxy平面に落としただけだね。データがよく広がっている方向をとらえられたという感じはしない。元々がスイスロールなので無理はあるんだけど。それに比べてカーネル主成分分析は、最初の2つの主成分でデータが広がっている方向をとらえることができたのかもしれない。非線形性を扱えるから、丸めたカーペットのように丸まったスイスロールを少し開くことができたって感じかな。

えっと、5ページの通常の主成分分析の復習をみると、通常の主成分分析というのは、データの空間の中で、すべてのデータをその単位ベクトルに正射影したときに正射影した後のデータたちの分散が最大になるような単位ベクトルの向きを求めて、それを第1主軸とするのですね。続けて第2主軸以降も求めるときは、第1主軸と直交する空間の中でそのようなベクトルを探していくと…それが「標本分散共分散行列 $V$ の大きい方から $d$ 個の固有値に対応する固有ベクトル」？ $u^{\top}Vu$ を最大化する $u$ を求めたいというのはいいですが、それが固有ベクトルというのはどういうことですか？？

落ち着いて追いかけようか。 $u^{\top}Vu$ を $u^\top u = 1$ の下で最大化したいわけだ。じゃあラグランジュ関数を $\displaystyle L(u, \lambda) = u^{\top}Vu - \lambda \left(u^\top u - 1\right)$ とおこう。これを $u$ で偏微分する。微分公式 $\displaystyle \frac{\partial}{\partial u} u^\top A u = (A + A^\top) u$ をつかえば $\displaystyle \frac{\partial}{\partial u} L(u, \lambda) = 2Vu - 2\lambda u$ だ。つまり、 $\displaystyle \frac{\partial}{\partial u} L(u, \lambda) = 0 \; \Leftrightarrow \; Vu = \lambda u$ になる。 $u$ は $V$ の固有ベクトルでなければならないね。それも、 $u^{\top}Vu = \lambda u^{\top} u =\lambda$ を最大化したいんだから、最大の固有値 $\lambda$ に対応する $u$ を第1主軸に選ぶべきだ。第2主軸以降はそれまでの軸と直交するように選びたいわけだけど、いま $V$ は対称行列だから固有ベクトルどうしが直交している（証明は以下などを参照してね）。

対称行列の固有値と固有ベクトルの性質の証明 | 高校数学の美しい物語

なるほど、ありがとうございます。6ページからは主成分分析を今度は特徴空間 $H$ で実行しようとしているんですね。先ほどは各データ $X_i$ を $u$ 方向に正射影した $u^\top X_i$ たちの分散を最大化しようとしていましたが、今度は $\langle f, \, \Phi(X_i)\rangle$ なるものの分散を最大化しようとしていますね。 $||f||=1$ の下で。

内積 $\langle \cdot, \cdot \rangle$ とノルム $||\cdot||$ さえ決まっている空間であれば、主成分分析はできるということだね。

それで、解は $\displaystyle f = \sum_{i=1}^N a_i \tilde{\Phi} (X_i)$ の形で探せば十分？？え、えっと、なぜこの形で十分かもわからないですが、 $f$ とは何なんですか？先ほど通常の主成分分析でデータの分散が最大となる向きの単位ベクトル $u$ を探したように、 $f$ も $H$ 内の単位ベクトルというわけではないんですか？これ、ベクトルなんですか？？

無論ベクトルだよ。でも部長はまだベクトルを「成分を縦に並べたもの」とイメージしているかな。ベクトルというのはあくまで「和やスカラー倍ができる集合の元」だ。それでしかない。そして「データの分散が最大となる向き」というのは、「各データとその単位ベクトルとの内積をとったものの分散が最大になるような単位ベクトル（ノルムが1のベクトル）」だ。この「向き」は、成分を縦に並べたものである必要はないよね。

そういうことですか…ではイメージを捨てて、内積で考えるようにしましょう。…すみません、部分空間と直交補空間とは何でしょう。

うーん、よく知っているベクトルのイメージに戻っちゃうけど、 $\mathbb{R}^3$ というベクトル空間を考えて、この空間の中のある平面だけみると、この平面は和とスカラー倍で閉じているから $\mathbb{R}^3$ の部分空間だ。直交補空間というのは、その平面に垂直な直線の中で閉じている空間だね。 $\displaystyle \left( \begin{array}{c} x \\ y \\ 0 \end{array}\right)$ とかけるベクトルたちの空間と $\displaystyle \left( \begin{array}{c} 0 \\ 0 \\ z \end{array}\right)$ とかけるベクトルたちの空間って感じかな。それでいま考えている話に戻ると、 $H$ という特徴空間の中には $\{\tilde{\Phi}(X_i)\}_{i=1}^N$ の和やスカラー倍ではつくれない「ベクトル」がある。 $\{\tilde{\Phi}(X_i)\}_{i=1}^N$ の和やスカラー倍でつくれない、というのは、 $\{\tilde{\Phi}(X_i)\}_{i=1}^N$ たちがつくる部分空間に射影したベクトルを差し引いてもゼロでないベクトルが残っているってことだね。ただ、もし $f$ というベクトルがそのようなゼロでないベクトルを含むようなものであったとしても、その差し引き残ったベクトルってあってもなくても $\tilde{\Phi}(X_i)$ との内積の値に影響しない。いま「データの分散が最大となる向き」 $f$ を探したいわけだけど、もし $f = f_0 \oplus f_{\bot}$ の $f_{\bot}$ がゼロでなかったとしよう。このとき $||f_0||^2 = ||f|| - || f_\bot ||^2 =1-|| f_\bot ||^2 < 1$ だけど、 $f' = 1/(1-|| f_\bot ||^2)^{1/2} f_0 \oplus 0$ とすれば、 $f'$ への射影の方が $f$ への射影よりデータの分散が単純に $1/(1-|| f_\bot ||^2)^{1/2}$ 倍大きくなるんだよね。いま $f$ のノルムは1という制約があるんだから、 $\tilde{\Phi}(X_i)$ との内積の値に影響しない成分に割り振ってる余裕はないってとこかな。

だから $\{\tilde{\Phi}(X_i)\}_{i=1}^N$ たちがつくる部分空間内で探せば十分、つまり、(1.6) 式の形で探せば十分ということですか。次元がよくわからない、というか次元という概念があるのかどうかもよくわからないベクトル空間でも、有限個の係数を探せばよいということになるんですね。そうなると、さっきとそっくりな解き方ができるんですね。しかし、先ほどと違って $a^\top \tilde{K}^2 a$ の $a$ というのはもはや「ベクトルの向き」を意味しませんね。そして、7ページの下部の式のように第 $p$ 主成分まで求まるんですね。これがカーネルPCA…。

（ノート2があれば）つづく

スクリプト

import numpy as np
import pandas as pd

df = pd.read_csv('swissroll.dat', sep='\s+', header=None)
df = df.apply(lambda x: x / x.std(), axis=0) # 標準化
df[1] = df[1] - df[1].mean() # y軸だけ中央がゼロでないのでシフト
print(df.head())
c = np.array(['tomato', 'dodgerblue', 'gold', 'mediumseagreen']).repeat(400) # 4色に色分け

# PCA
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(df)
df_pca = pca.transform(df)

# KernelPCA
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel='rbf', gamma=1.5)
kpca.fit(df)
df_kpca = kpca.transform(df)

# プロット
%matplotlib inline
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['font.size'] = 16

x = np.array([-10, 10])

fig, axes = plt.subplots(ncols=2, figsize=(12, 5), sharex=True, sharey=True)
axes[0].scatter(df.iloc[:,0], df.iloc[:,1], c=c)
axes[0].plot(x, x * pca.components_[0][1] / pca.components_[0][0], c='black', linestyle='solid', linewidth=2) # 第1主成分
axes[0].plot(x, x * pca.components_[1][1] / pca.components_[1][0], c='black', linestyle='dotted', linewidth=2) # 第2主成分
axes[0].set_xlim([-3, 3])
axes[0].set_ylim([-3, 3])

axes[1].scatter(df.iloc[:,0], df.iloc[:,2], c=c)
axes[1].plot(x, x * pca.components_[0][2] / pca.components_[0][0], c='black', linestyle='solid', linewidth=2) # 第1主成分
axes[1].plot(x, x * pca.components_[1][2] / pca.components_[1][0], c='black', linestyle='dotted', linewidth=2) # 第2主成分

plt.subplots_adjust(wspace=0.15)
plt.show()

fig, (axL, axR) = plt.subplots(ncols=2, figsize=(12, 5))
axL.scatter(df_pca[:,0], df_pca[:,1], c=c)
axR.scatter(df_kpca[:,0], df_kpca[:,1], c=c)
plt.show()