機械学習のための特徴量エンジニアリング：ノート1

以下の本を読みます。キャラクターは架空のものです。解釈の誤りは筆者に帰属します。お気付きの点がありましたらコメント等でご指摘いただけますと幸いです。

機械学習のための特徴量エンジニアリング ―その原理とPythonによる実践 (オライリー・ジャパン)

作者: Alice Zheng,Amanda Casari,株式会社ホクソエム
出版社/メーカー: オライリージャパン
発売日: 2019/02/23
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

正誤表リンク： https://www.oreilly.co.jp/books/9784873118680/

次回：まだ

f:id:cookie-box:20190101160814p:plain:w60

面白そうなテーマの本だね。なんで読もうと思ったの？

f:id:cookie-box:20190101155733p:plain:w60

会社…じゃなかった、教室の本棚に補充されてたので。ほら、オライリーのコーナーに。

教室の本棚のラインナップおかしいよね。

以前 Kaggle の期間限定イベントを走ってみたことがあるんですが、そのとき気付いたことがあったんですよね。

コンペティションに参加って言おうよ。

機械学習においてデータの前処理というと、

自然言語データのようなそもそも数値でないデータを、その性質が保持された何らかの数値にする。
欠損がある特徴の欠損部分を何らかの方針で埋める／欠損がある特徴やレコードを削る。

というような「そもそも数値でないものを数値にする」イメージだったんです。しかし、Kaggle の Kernel ではそのようなケース以外にも、

「勤続年数」を「年齢」で割る（座標変換）。
「支払期限日」から「実際に支払いがあった日」を引く（座標変換）。
ある特徴量（あるいは被説明変数）を対数変換する（座標変換）。
特徴量 V_1～V_N の最小値／平均値／最大値をとる（要約）。
全ての特徴量の和がゼロかどうかを追加する（要約）。
特徴量 V_1～V_N を PCA, t-SNE, SparseRandomProjection などでM次元に削減した特徴量 V'_1～V'_M に置き換える or 元の特徴量群に追加する（要約）。
まずランダムフォレスト回帰してみて重要度が上位 K 件の特徴量に絞る（削減）。
学習データと評価データで分布が異なる特徴を削る（削減）。

というように「元々数値であってもmodifyする」ということもしていたんですよね（カッコ内は今適当にラベリングしてみただけです）。このような前処理は「機械学習の代表的な方法はディープラーニングである」「ディープラーニングは表現定理により任意の関数を表現できる」ということを紙の本で勉強してきた人にとってはなかなか違和感がないですか？こちらが座標変換やら要約やら削減やらしなくても、ディープラーニングがおのずから理想の変換をしてくれるはずなのですから。特徴をわざわざ絞り込むというのも不思議です。しかし、現実に計算機で学習するとなると計算資源は有限なので特徴量をほどよく削減する必要があり、効率的によい解にたどり着いてくれるように座標変換や要約する必要があり、そもそもディープラーニングでないモデルの方が有効な場合があり、人類はこのような特徴量エンジニアリングをせっせとしなければならないというフェーズにいたということなんですね…私はてっきり非数値データの数値データ化以外何もしなくていいと思っていたのに…ディープラーニングに完全に騙されました…。

ディープラーニングにそんなに幻想抱いてたの！？

しかし嘆いてばかりもいられません。特徴量エンジニアリングの方法を習得しなければ。1章の内容は大丈夫ですね。2章の5ページの下の方、「その他にも結果が入力特徴量のスケールに影響を受ける手法として、k-means クラスタリング、（後略）」とありますが、よくわかりません。これらの手法は入力データセットが変われば普通に結果が変わるものではないですか？スケール云々ではなく。

…こういうことが言いたいんじゃないかな？現実的ではない例だけど、まとまった「金額たち」を受け取って、個々の金額に「この金額は安い方です」「この金額は高い方です」という判定を返すモデルを k=2 の k-means クラスタリングで実現するとする。このモデルに「10円、1000円、10000円」という金額たちが入力されたとすると、1000-10=990 の方が 10000-1000=9000 より小さいから、真ん中の「1000円」は「安い方」という判定だ。でもこれが、実は運用システム上では金額の常用対数が取られていたとすると、入力は「log(10)=1、log(1000)=3、log(10000)=4」となって真ん中の「log(1000)」は「log(10000)」側に近い、「高い方」という判定になる。入力データに「円」という物差し（スケール）を当てるか、「円のlog10」という物差しを当てるかで結果が変わる。だから、5ページが言いたいのは、真ん中の段落と合わせて、数値データの「粒度は適切か？」「物差しは適切か？」を確認しましょうということだと思うよ。

なるほど。であれば、6ページで言及されている、分布を確認して対数変換などするというのも「物差しは適切か？」に含まれる気がしますね。もちろん、決定木を用いるなら対数をとるという単調変換に意味はないので、「物差しは適切か？」も用いる手法によりますが…。8ページの「データ空間」というのは聞き慣れないです。図2-2 の左側と右側はそれぞれデータを以下のように捉えているだけではという気がするのですが。

	歌1	歌2	歌3
ユーザ1	好き	好き	嫌い
ユーザ2	好き	嫌い	嫌い
ユーザ3	嫌い	好き	嫌い
ユーザ4	好き	好き	嫌い

	ユーザ1	ユーザ2	ユーザ3	ユーザ4
歌1	好き	好き	嫌い	好き
歌2	好き	嫌い	好き	好き
歌3	嫌い	嫌い	嫌い	嫌い

「歌1が好きなユーザは歌2も好きな可能性が高い」などというパターンを学習したいなら左側のようにデータを捉えるのではないかと思います。未知のユーザがどんな歌を好きか予測したいというイメージです。右側のデータだと「ユーザ1に好かれる歌はユーザ2にも好かれる可能性が高いがユーザ3には好かれない可能性が高い」というパターンを学習することになりそうなので、「未知の歌がどんな層に受けてどんな層に受けなさそうか」というイメージですかね。よくわからないですが置いておきます。

2.2.1節は、「何を予測することを目指すのか」といった話ですね。2.2.2節は…「あるレストランのレビュー件数だけはわかっているが評価点数はわからないので予測したい」って状況はない気がするんですが…。何にせよ、特徴量の離散化＝粒度を粗くすることって、これも対数変換同様、決定木を用いるのであったら原理上は関係ないですよね。

でも、それ以上細かくみることに意味がないと強く信じられる状況なら、粒度を粗くすることで、学習が軽くなって色々なハイパーパラメータを試せるとかあるかもしれないよ。

まあ確かに。2.3.1 節の例、21ページに対数変換が上手くいった理由がかいてあるようですが、説明がなんかふわふわしているんですが…。

結局図2-9の上図より下図の方がまだ直線でフィッティングしやすいってことじゃないのかな…どのみち決定係数がマイナスな例だしそこをあまり深く考えなくていいと思うけど…。

2.3.2節は、より一般的な変換ですね。分散を安定化するとはどういうことで、何のためにすることなのかよくわかりません。確かに、色々な母平均のポアソン分布からサンプル群を取り出してみて「サンプル群そのもの」「サンプル群の平方根をとったもの」の平均と分散をプロットしてみると、平方根を取った場合に分散が平均に拠らなくなるようにはみえますが（下図のオレンジ色の方が平方根を取った場合ですね）。

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 5, 5
rcParams['font.family']='IPAGothic'
rcParams['font.size'] = 16

size = 10000
list_mean = []
list_var = []
list_mean2 = []
list_var2 = []

for lam in np.arange(1, 11, 1):
    x = np.random.poisson(lam=lam, size=size)
    list_mean.append(np.mean(x))
    list_var.append(np.var(x))
    list_mean2.append(np.mean(np.sqrt(x)))
    list_var2.append(np.var(np.sqrt(x)))

plt.scatter(list_mean, list_var)
plt.scatter(list_mean2, list_var2)
plt.xlabel('サンプルの平均')
plt.ylabel('サンプルの分散')
plt.show()

f:id:cookie-box:20190311160609p:plain:w270

…もしその特徴がポアソン分布から生成されると信じているなら、 $f(x) = \sqrt{x}$ という変換をほどこすことで分散が期待値と（ほぼ）独立になるようにできるということだと思うけど…独立でなかったら直接的にどう悪いのかというのはよくわからないな…どちらかというと、期待値と分散が独立でないような分布は正規分布に近くなく裾が重かったりして線形回帰モデルなどを適用する上で具合が悪い、ということが問題視されているようにもみえる。モチベーションは分散安定化というより正規分布に近づけることと考えた方がいいんじゃないかな。24ページの訳注にもポアソン分布の場合には分散安定化変換になるっていう書き方がしてあるし…。

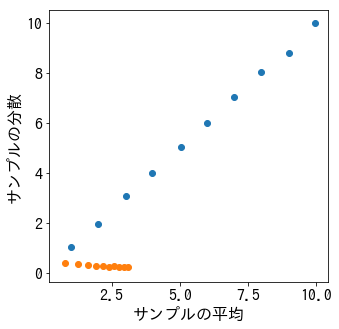
なるほど…。2.4節は大丈夫そうですが…33ページの注意事項、「図2-17は、特徴空間ではなくデータ空間であることに注意してください」というのは、（8ページの例に即していうと）各点がユーザではなく歌ということですか？なぜユーザではないんでしょう？ 3.1.1節を読んだ方がよさそうですが…2.5節の内容も大丈夫ですね。2.6節は…38ページの相互情報量というのは？

ウィキペディアによると $\displaystyle I(X; Y)=\sum_{y \in Y}\sum_{x \in X} p(x, y) \log \frac{p(x,y)}{p(x)p(y)}$ という量みたいだね。あらゆる $(x,y)$ の組について、 $X$ と $Y$ が独立だとした場合の同時分布のビット数から、 $X$ と $Y$ の実際の同時分布のビット数を差し引いたものの平均だね。もし $X$ と $Y$ が独立なら $I(X; Y)$ はゼロだ。逆に $X$ と $Y$ が全く同じ確率分布にしたがうなら $I(X; Y)$ はその確率分布のビット数の平均そのものになる。もし $X$ と $Y$ が独立なら、 $(x,y)$ の $x$ が珍しい出来事だったとき $y$ まで珍しい出来事という確率は相当低い。だからそんな $(x,y)$ の組に割り振るビット長はとても大きくなる。でも $X$ と $Y$ が独立でなかったら $x$ も $y$ も珍しい出来事である確率がもっと高くなるかもしれない。だから同じ $(x,y)$ の組に割り振るビット長がより小さくなる。ただし $(x,y)$ が起きる確率は $x$ が起きる確率より高くなることはないから、 $x$ に割り振るビット長よりは小さくならない。つまり $I(X; Y)$ は $N$ 点の $(x,y)$ を記録するときに $N$ 点の $x$ と $N$ 点の $y$ を別々に記録するときよりどれだけディスク容量が節約できるか（1点あたり）という量だね。 $X$ と $Y$ が相互に依存するほどディスク容量が節約でき、 $I(X; Y)$ は大きい。

いまに始まったことではないですが、その説明は私的言語すぎて誰にも伝わりませんね…。ラッパー法というのは特徴の組み合わせの総当たりといった感じなのですかね。以下の記事によると、特徴を増やしていく方法と減らしていく方法とあるようですが。

特徴選択とは？機械学習の予測精度を改善させる必殺技「特徴選択」を理解しよう

2章をまとめると、「粒度は適切か？」「物差しは適切か？」「組み合わせるべきではないか？」「絞り込めないか？」といったところでしょうか。

3章はテキストデータの取り扱いだね。

raven ってカラスなんですか？ crow とはまた違う種類のカラスなんですね…はっ、ハリーポッターのレイブンクローとはカラスカラスという意味だったんですね？？

いや、レイブンクローのクローは調べたらかぎつめ（claw）らしいけど…。

文章を「どの単語が何回出現するか」のみに着目してベクトル化する、という方法が最初にありますね。ここでデータ空間が出てきますね…図3.5は、「各データの『猫』という特徴量はどうなっているか」というベクトルをあらゆる特徴量について求めてプロットしたもので、単語空間ではなく文章空間なんですよね。いや両者が転置の関係なのはわかりますが、結局何のためにデータ空間を考えるんです？

4章でも出てくるみたいだね。4章で扱う TF-IDF では「『猫』という単語の出現回数が全単語の出現回数に占める割合」「『猫』を含む文書数」が要るから、各レコードが単語で各カラムが文章であるデータに、「元データの各行ベクトルの和を全データの和で割ったもの」「元データの各行ベクトルの非ゼロ要素の個数」という2つの新しい特徴量のカラムを加えるとかそんなイメージかな。目的は文章の特徴量を得ることだけど、そのために各単語の特徴量を得たくて、各単語の特徴を得るのに文章中への出現っぷりをみたくて、説明-被説明関係がくるくるするみたいな？

54ページにコロケーションという概念が出てきますね。日本語のコロケーションの例ってどんなのがあるでしょう？

2語以上組み合わせることで、各単語を単に組み合わせたのとは異なる意味が生じるってことだよね。そのまま慣用句になっちゃうけど、「顔が広い」「猫の額」とかかな？もっと日常語でもありそうだけど…。

4章まできましたね。TF-IDF の話です。IDF は一部の文書にしか出現しない単語に重みを付けるのですね。IDF は対数を取った方が一部の文章にしか出現しない単語の影響が大きくなるということですが、どちらかというと多くの文章に出現する単語の影響が小さくなるということでしょうか…。67ページの、「TF-IDF に $\ell^2$ 正規化を行った際の結果は、 $\ell^2$ 正規化を単体で使う場合と同じです」ってどういう意味でしょうか？

これは文章区間で各単語を超球上に配置させるってことかな。だったら、TF-IDF を $\ell^2$ 正規化したら Bag-of-Words の $\ell^2$ 正規化と一緒ってことなのかも。一部の文書にしか出現しない単語に重みを付けたのが正規化でかき消されてしまうから。どの軸で正規化してるのかちゃんと再現実行して確かめてみないとわからないけど…。

70ページに、「劣決定（underdetermined）とよばれ、そのままでは解くことができません」とありますが、解けないケースなんてあるんですか？

学習データが10点で特徴が100個あったとして、線形モデルを考えたら、切片を無視すれば重みは100個あるけど、連立方程式は10個。足りないよね。

確かに。

つづきは後で