雑記： 沖本本読み勉強会用のメモ

以下の本を読む勉強会用のメモです。もし何か誤りがありましたらご指摘いただけますと幸いです。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) 沖本 竜義 朝倉書店 2010-02-01 売り上げランキング : 19813 Amazonで詳しく見る by G-Tools

今度勉強会で上の本の3章を発表することになりました。

へー。1章と2章は読んだの？

読んでないです。

読もうよ！？

仕方ないですね…1章で思い出しておきたい事項は以下でしょうか。

• 時系列分析では時系列データの背後にデータ生成過程（または単に過程）を仮定する。
• 期待値が時刻tに依存せず一定で、自己共分散も時刻tに依存せずラグkにのみ依存するような過程を弱定常であるという。
• 特に、ある長さkの部分時系列の同時分布が時刻tに依存せず同一の分布にしたがうような過程を強定常であるという。
• 正規過程が弱定常であれば、強定常である。
• 期待値が時刻tに依存せずゼロ、0次の自己共分散（つまりただの分散）が時刻tに依存せず一定、1次以上の自己共分散が時刻tに依存せずゼロであるような過程をホワイトノイズという。
• データの自己相関の有無を判断するには、以下のような検定をする。
• ある次数の標本自己相関係数に対して「=0」の帰無仮説を「≠0」の対立仮説に対して検定する。
• ある次数までの全ての標本自己相関係数に対して「全て0」の帰無仮説を「どれかは0でない」の対立仮説に対して検定する。

…9ページの脚注がよくわかりません。正規過程とは、ある長さkの部分時系列が多変量正規分布にしたがう（多変量正規分布の期待値と共分散は時刻に依存してもよい）ような過程なんですよね。任意の時刻tに対して y_t の周辺分布が正規分布ならば、そのような過程は正規過程なのではないでしょうか？ それぞれ正規分布にしたがう確率変数をいくつか並べたら、その確率ベクトルは多変量正規分布にしたがいますよね？

とは限らないかな。例を示そうか。

n <- 20000
breaks <- seq(-10,10, 0.5)
layout(matrix(c(1,1,2,3,4,4,5,6,7,7,8,9), 4, 3, byrow=FALSE))

MyPlot <- function(x, y) {
plot(c(-10,10), c(-10,10), xlab="x", ylab="y", type="n")
 abline(h=0, v=0, lty=2)
 points(x, y)
 hist(x, breaks=breaks)
 hist(y, breaks=breaks)
}

### case 1 ###
x <- rnorm(n=n, mean=0, sd=2.0)
y <- rnorm(n=n, mean=0, sd=2.0)
MyPlot(x, y)

### case 2 ###
library(mvtnorm)
mu <- c(0, 0)
Sigma <- matrix(c(4, 3.6, 3.6, 4), 2, 2)
xy <- rmvnorm(n, mu, Sigma)
x <- xy[,1]
y <- xy[,2]
MyPlot(x, y)

### case 2.1 ###
x0 <- x[x < -3 | 3 < x]
y0 <- y[x < -3 | 3 < x]
x1 <- x[!(x < -3 | 3 < x)]
y1 <- y[!(x < -3 | 3 < x)]
x1a <- x1[x1 < 0]
x1b <- x1[!(x1 < 0)]
MyPlot(c(x0, x1a, x1b), c(y0, y1))

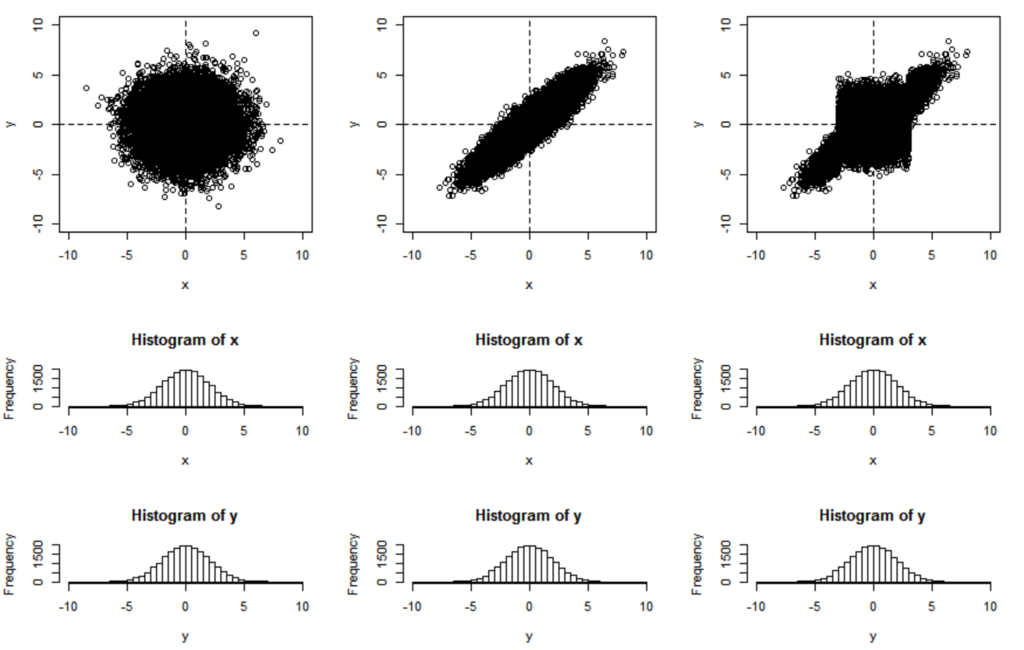
上の3つの例はどれもXの周辺分布が N(0, 4)、Yの周辺分布も N(0, 4) だけど、一番右のプロットの形状は2変量正規分布にみえる？

一番右のプロットの形状ですか？ 気持ち悪いです。

ごめん…。

次は2章ですね。ここでMA過程とAR過程が降って湧いたように基本的なモデルとして登場しますが、さもそれらが自己相関をもつ確率過程を表現しようとした自然な帰結なのだというような雰囲気ですが、自己相関をもつ確率過程を表現するのに「y_{t} と y_{t-1} が共通の確率変数に依存する」と「y_{t} が y_{t-1} を参照する」以外のモデルは本当にないんでしょうか？ y_{t-1} が y_{t} を参照するとか。

未来の値が現在の値を決定するモデルはやめようよ？

データ生成過程さんにしてみれば、エントロピーの増大方向など知ったことではなくないですか？

仮にデータ生成過程さんが気にしなくても、そのモデルを利用する我々が気にするんだよ！

なるほど。…それで本に戻ると、MA過程の方は次数・パラメータにかかわらず定常であると。これは直感的に理解できますね。有限の過去までのノイズの線形結合で爆発しようがありませんから。それでAR過程の方は (2.15) 式の全ての解の絶対値が1より大きいときに定常となると。なぜそうなるかのやわらかい解釈は 2018-03-07 の記事を参照してください。また、MA過程の問題点として、ある過程を記述する係数とホワイトノイズの分散のセットの候補が複数存在してしまうので、AR(∞)過程に書き直せる（＝反転可能である）ものを選択しようという基準があるということですね。

「同一の期待値と自己相関構造をもつMA(q)過程が2^q通り存在し、その内1つのみが反転可能である」というのをきちんと追えてないけど、「MA過程はAR(∞)過程に書き直せる」「だから少なくともAR(∞)過程に書き直せるようなホワイトノイズの取り方が1つ存在する」というのは理解できるかな。

2章の後半はモデルの推定と解釈の話ですが…43ページに、ARMAモデルやGARCHモデル、マルコフ転換モデルなどは最小2乗推定できないってありますけど、なんででしょう？ 何かモデルを仮定すれば残差平方和を計算することは常にできますよね？

まずARMAモデル（というよりMAモデル）については、ある時刻での残差が次の時刻の説明変数になっちゃうよね。だから「理想的には残差がゼロだろう」っていうスタンスのOLSで推定したら駄目だよね。GARCHとマルコフ転換モデルはもっと後の方で出てくるからすぐ追えないけど、GARCHはぶれの大きさをモデリングするし、マルコフ転換モデルは観測できない真の状態がぶれるモデルだし、やっぱり「理想的にはぶれないだろう」っていうOLSの考え方はそぐわないようにみえる。

あー、確率的な変動が全くないとすると意味をなさないようなモデルだと駄目っぽいですね。それでやっと3章に辿り着きましたが、この章のタイトルは「予測」です。しかし予測とは何なのかと。

大切な問いだね。

AR(1)過程を例に挙げてこれを問うていますが…「AR(1)過程と現時点の観測値を所与とする。次の時点の予測値とは何か」と。「予測A」はAR(1)過程の期待値そのものを予測値としていて、入手している現時点の観測値を完全に無視していくスタイルですね。「予測B」はノイズの最頻値、「予測C」はノイズの平均値が次の時刻に実現するだろうというような予測です。別にどの予測もそういう予測ではあるわけですが、ここでは（一期前までに観測される値が所与の下での）予測誤差の2乗の期待値が小さいほどよい予測とし、予測誤差の2乗の期待値を最小にする予測を最適予測とよぶということです。それで、先の例では「予測C」が最適予測だと…ん、A～Cの3つの予測の中では「予測C」が最もよいというのはわかるんですが、「予測C」よりもよい予測はないことは示されてないですよね？

「予測C」が「一期先の値の期待値を予測値とする」として得られたことは、それが予測誤差の2乗の期待値を最小に予測であることの説明になってないってことかな。 を について微分してみたらどうだろう？

思い出しました。2次損失は期待値で最小に、線形損失は中央値で最小に、0-1損失は最頻値で最小になるとかDLMの本でやりましたね。…その後は、AR過程の何期も先のMSEを陽に書くのは難しい、区間予測はシミュレーションでやろう、というような話ですね。…なんか3章はそんな感じですね。

（次回があれば）つづく