以下の論文を読みます。

えっと、LSTM がもてる記憶の複雑さ―つまり、同時にもてる情報量の大きさと特徴抽出の深さ―を上げるにはどうしようって話だったよね。単純に記憶の次元を増やすのじゃパラメータが激増するし、LSTM のスタックじゃせっかくの LSTM の利点である長期依存性の学習が台無しになっちゃうって言ってたよね。


じゃあそのどちらか、あるいは両方を採用するとか?

それは…後者を。パラメータの再利用なら、特徴量ベクトルの次元数とは独立にパラメータ数を決められるし(CNNでいうと、画像の大きさとは関係なくカーネルサイズを決められる、かな…)、あと、情報をばらばらにして再帰ループさせることができるから、特徴抽出の深化に役立つって。これは、詳しくは後で? あと、それとは別に…RNNの隠れ状態ベクトル(特徴量ベクトル)をテンソルで表すって。あ、この論文では LSTM を拡張するけど、先に RNN で考える? テンソルで表すと、パラメータを共有する軸?をつくれるって。この軸と垂直な方向に隠れ状態テンソルを延ばしても、パラメータ数は増えない。これは、CNNでいう畳込み層のパラメータ数が、カーネルサイズが同じなら画像のサイズを大きくしても変わらないのと同じ。あと、高階のテンソルをつかうと、パラメータ数が同じなら、depth の割に高速にネットワークを wide にできるって。あの、「同時にもてる情報量の大きさ」と「特徴抽出の深さ」と言っていたのを、原文通りに width と depth とかくようにするね…正確ではない訳だと思うから。この、テンソルにする理由の後者はまだよくわからない。

うん。その隠れ状態のテンソルは具体的にどんな風に計算されてつくられるものなのか…プログラムでもなければ、よくわからないかな。

泉さんには、プログラムの方が読みやすい? でも、論文だから…数式。あ、RNNの隠れ状態ベクトルをテンソルにするといったけど、最初は簡単のために2次元のテンソル、つまり行列で考える。まず、普通の Stacked RNN (sRNN) からスタートする。論文3ページの Figure 1 の (a) …下に、絵を描いた。破線の左側。sRNN はある時間ステップ内で多段階の特徴抽出をする。図の例だと、3段階? この特徴抽出を、ある時刻に一段階目、次の時刻に二段階目…としたい。RNN は既に時間方向に「深い」から、特徴抽出も、これに便乗? そのように特徴抽出を時刻ごとに一段階ずつにしたのが、破線の右側。Figure 1 の (b) …これは skewed sRNN といって、sRNN をゆがめただけで…既に過去に別の論文で提案されている…。


確かに、右側の絵では、データがどんどん次の時刻に流れて行っているね。出力される の上の添え字は何段目の RNN の隠れ状態ベクトルか、下の添え字はどの時刻の入力まで参照しているかという意味?

合ってる。上の図を、時間方向に展開しない形で書くと、下図になる。下図の一番左が sRNN で、真ん中が skewed sRNN。skewed sRNN の一層目は、一つ前の時刻の入力データと、一つ前の時刻の一層目の出力を受け取る。でも、一つ前の時刻の二層目以降の出力を受け取ってもいい。二層目の出力も受け取ったのが、下図の一番右。そして、この一番右の図の、各層の隠れ状態ベクトルを束ねた行列を隠れ状態テンソルと見做したものが、Tensorized RNN (tRNN)。



なるほど。これなら、 を大きくしてもパラメータは増えないし、時の流れに便乗して特徴抽出の深化が進む…cross-layer convolution で層間でデータを相互作用させることで、複雑な学習もできる…後はこれを LSTM よろしく、記憶とゲートを増設するだけって感じかな?

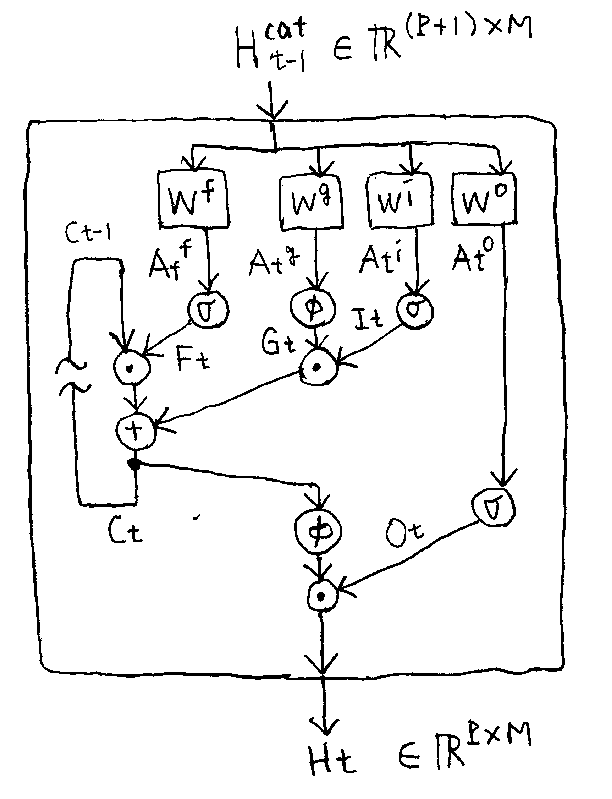
基本的には…。でも、記憶とゲートを増設するだけでは、上手くいかないことが…。単純に記憶とゲートを増設すると以下。これは、Figure 1 の (d) に相当。ただこれだと、記憶は時間方向にしかスムーズに逆伝播しない。いま、cross-layer convolution しているから、層をまたぐ方向にも記憶は伝播しないといけない…。