2021-03-28

Time Series Analysis：ノート10章弱定常ベクトル過程（その2）

本読み

以下の本の10章を読みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

Time Series Analysis

作者:Hamilton, James D.
発売日: 1994/01/11
メディア: ハードカバー

その他の参考文献

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) | 竜義, 沖本 |本 | 通販 | Amazon

関連記事

f:id:cookie-box:20190101155733p:plain:w60

結局前回は以下のことしかやっていませんね…。

p 次ベクトル自己回帰過程 VAR(p) を導入してその定常条件を確認した。
定常 VAR(p) は Vector MA(∞) にかき直せる。
一般に定常ベクトル過程の自己共分散行列 $\Gamma_{\nu} = E \bigl[ ({y}_t - \mu)({y}_{t - \nu} - \mu)^\top \bigr]$ は $\Gamma_\nu^\top = \Gamma_{-\nu}$ となる。

では、次は VAR(p) の自己共分散行列 $\Gamma_\nu$ が具体的にどうなるかみていくのでしょうか？

f:id:cookie-box:20190101160814p:plain:w60

いいや、ここで改めて q 次ベクトル移動平均過程 Vector MA(q) $y_t = \mu + \varepsilon_{t} + \Psi_1 \varepsilon_{t-1} + \cdots + \Psi_q \varepsilon_{t-q}$ を導入しているね。その自己共分散行列をみている。

え、ここで Vector MA(q) を導入するんですか？既に前回 Vector MA(∞) がフライングで出てきていましたが…まあいいです、試しに Vector MA(2) の自己共分散行列を計算してみましょう。

$\begin{split} \Gamma_{\nu} &= E \bigl[ ({y}_t - \mu)({y}_{t - \nu} - \mu)^\top \bigr] \\&= E \bigl[ ( \varepsilon_{t} + \Psi_1 \varepsilon_{t-1} + \Psi_2 \varepsilon_{t-2} )(\varepsilon_{t- \nu} + \Psi_1 \varepsilon_{t- \nu-1} + \Psi_2 \varepsilon_{t- \nu-2} )^\top \bigr] \\&= E \bigl[ ( \varepsilon_{t} + \Psi_1 \varepsilon_{t-1} + \Psi_2 \varepsilon_{t-2} )(\varepsilon_{t- \nu}^\top + \varepsilon_{t- \nu-1}^\top \Psi_1^\top + \varepsilon_{t- \nu-2}^\top \Psi_2^\top ) \bigr] \end{split}$ これは…ベクトルホワイトノイズ $\varepsilon_t$ は時刻の添字が一致するときに限り共分散が零行列でない $\Omega$ となりますから…結局以下になりますね。 $|\nu| > 2$ では $\Gamma_\nu = 0$ です。 $\begin{split} \Gamma_{-2} &= \Omega \Psi_2^\top \\ \Gamma_{-1} &= \Omega \Psi_1^\top + \Psi_1 \Omega\Psi_2^\top \\ \Gamma_0 \, \, &= \Omega \quad \, \,+ \Psi_1 \Omega\Psi_1^\top + \Psi_2 \Omega\Psi_2^\top \\ \Gamma_1 \, \, &= \quad \, \, \qquad \Psi_1 \Omega \quad \, \, + \Psi_2 \Omega\Psi_1^\top \\ \Gamma_2 \, \, &= \quad \, \, \qquad \qquad \qquad \; \; \Psi_2 \Omega \end{split}$ $\Gamma_\nu$ は $\nu$ ステップ昔の自分との共分散でした。Vector MA(2) は現在のノイズ、1ステップ昔のノイズ、2ステップ昔のノイズからなります。 $\Gamma_2 = \Psi_2 \Omega$ は、「現在の自分の2ステップ昔のノイズが、2ステップ昔の自分の現在のノイズと相関する項」ですね。 $\Gamma_{-2} = \Omega \Psi_2^\top$ は、「現在の自分の現在のノイズが、2ステップ未来の自分の2ステップ昔のノイズと相関する項」です。そして3ステップ以上ずれた自分とは相関がなくなります。

まあそうなるよね。じゃあ Vector MA(∞) の自己共分散行列はどうなる？ただし係数行列 $\Psi_{\nu}$ は絶対総和可能とするよ（前回明示的に「成分ごとに絶対総和可能」とかいたけど、以降テキストの表記にならって「成分ごとに」を省くよ）。ちなみに単変量の MA(∞) は係数が絶対総和可能であるという条件の下で定常過程だったね（52ページ）。

Vector MA(∞) とはいきなり次数が増えましたね…そうなると何ステップずれても相関はありますよね…。まあ順に考えると、

0次の自己共分散行列は $\Gamma_0 = \Omega + \sum_{\nu' = 1}^{\infty} \Psi_{\nu'} \Omega\Psi_{\nu'}^\top$ になりますね。
1次の自己共分散行列は $\Gamma_1 = \Psi_1 \Omega + \sum_{\nu' = 1}^{\infty} \Psi_{\nu' + 1} \Omega\Psi_{\nu'}^\top$ になります。
2次の自己共分散行列も $\Gamma_2 = \Psi_2 \Omega + \sum_{\nu' = 1}^{\infty} \Psi_{\nu' + 2} \Omega\Psi_{\nu'}^\top$ になります。
では、-1次であったら $\Gamma_{-1} = \Omega \Psi_1 + \sum_{\nu' = 1}^{\infty} \Psi_{\nu'} \Omega\Psi_{\nu' + 1}^\top$ になります。
-2次であったら $\Gamma_{-2} = \Omega \Psi_2 + \sum_{\nu' = 1}^{\infty} \Psi_{\nu'} \Omega\Psi_{\nu' + 2}^\top$ になります。

…このようになるはずですが、これらの自己共分散行列は値をもつのでしょうか？係数行列 $\Psi_{\nu}$ が絶対総和可能であるといっても、ただちにこれらが有限の値をもつことにはなりませんよね？もし発散してしまったら Vector MA(∞) は定常過程にならないのでは？

$\Gamma_s$ は有限の値をもつよ。もっというと絶対総和可能になる。証明は Appendix にあるけど、いきなり $\Gamma_s$ の $i, j$ 成分 $\gamma_{i,j}^{(s)}$ が有限であることを考えるのはややこしいから、まず以下の2つの積の期待値を考えよう。あ、以下 $\Psi_0 \equiv I_n$ とするよ（部長がかき下した自己共分散行列もこう定義すればもっとすっきりする）。

$z_t(i,l) = \sum_{\nu= 0}^{\infty} \psi_{i, l}^{(\nu)} \varepsilon_{t-\nu, l}$ ： $y_t$ の第 $i$ 成分の、ノイズの第 $l$ 成分に依存する項。
$z_{t-s}(j,m) = \sum_{\nu= 0}^{\infty} \psi_{j, m}^{(\nu)} \varepsilon_{t-s-\nu, m}$ ： $y_{t-s}$ の第 $j$ 成分の、ノイズの第 $m$ 成分に依存する項。

これらの積の期待値をつかって自己共分散行列の成分が $\gamma_{i,j}^{(s)} = \sum_{l=1}^n \sum_{m=1}^n E\Bigl[ z_t(i,l)z_{t-s}(j,m) \Bigr]$ とかけるからこれが絶対総和可能であることを示そう。

それらの積の期待値ですか…やはりベクトルホワイトノイズの定義から異なるステップのノイズの成分どうしの積の期待値は0ですから、 $\sum_{\nu= 0}^{\infty} \psi_{i, l}^{(\nu + s)} \psi_{j, m}^{(\nu)} \omega_{l, m}$ でしょうか。ベクトルホワイトノイズの自己共分散行列 $\Omega$ の成分を $\omega_{l, m}$ としました。これが絶対総和可能かといわれると、 $\sum_{s= 0}^{\infty} \sum_{\nu= 0}^{\infty} | \psi_{i, l}^{(\nu + s)} \psi_{j, m}^{(\nu)} \omega_{l, m} |$ $\leqq |\omega_{l, m}| \sum_{\nu= 0}^{\infty} \sum_{s= 0}^{\infty} |\psi_{i, l}^{(\nu + s)}| |\psi_{j, m}^{(\nu)} | < \infty$ より絶対総和可能ですね…であれば各項は有限です…では、Vector MA(∞) は係数行列が絶対総和可能であるという条件の下で定常（ $t$ に依存せず $s$ のみに依存する有限の自己共分散行列をもつ）というわけですか。

ちなみに同じ要領で、もしベクトルホワイトノイズが有限な4次モーメントをもつなら、係数行列が絶対総和可能な Vector MA(∞) の4次モーメントも有限であるといえる（命題 10.2 の (c)）。これは $y_{i,t} y_{j,t-s} - E(y_{i,t} y_{j,t-s})$ が一様可積分といっていることに他ならない（命題 7.7 の (a)）。というわけで、193ページの議論と同様に、2次モーメントがエルゴード的であることがいえる（命題 10.2 の (d)）。

な、なるほど…？いやに Vector MA(∞) の性質を掘り下げますね…今後 Vector MA(∞) をそんなに使っていくんですか？項数が無限にあったら使いづらいと思うんですが…。

思い出してよ、定常 VAR(p) は Vector MA(∞) にかき直せたでしょ？だからこれらは定常 VAR(p) の性質に他ならないよ。そして、ここで2次モーメントのエルゴード性が確認できたことは定常 VAR(p) の標本から色々な推定や検定をすることの土台になる。

あっ…いやでも、それをいうには定常 VAR(p) が「係数行列が絶対総和可能な」Vector MA(∞) にかき直せることを示さなければ。

示せるよ。前回 VAR(p) の定常条件を示すのに、1次の差分方程式 $\xi_t = F \xi_{t-1} + v_t$ に持ち込んで $F$ を対角化 $F=T \Lambda T^{-1}$ したけど、VAR(p) の Vector MA(∞) 表現における係数行列はこの $F$ の $\nu$ 乗の左上 $n \times n$ ブロックだったでしょ？ $F^\nu =T \Lambda^\nu T^{-1}$ の任意の成分は263ページの一番下の式の形にかけるから（テキストでは $\nu$ じゃなく $s$ になっているけど）、これの $s=1, 2, \cdots$ についての和は収束するよね。

確かに。VAR(p) の定常条件は「どこかの時刻で発生したぶれが爆発しないでゼロに収束してほしい」といったものでしたが、それは「Vector MA(∞) 表現における係数行列が絶対総和可能であってほしい」と同じであったというわけですか…過程の爆発を防ぐために、VAR(p) はある時刻のノイズを再帰してしまうのでその拡大率を1未満にする必要があり、Vector MA(∞) はある時刻のノイズを再帰はしないが過去すべての時刻のノイズを取り込むので係数行列を絶対総和可能にする必要があると…。

10.2 節の続きには、 $n$ 変量 Vector MA(∞) を変換して $r$ 変量両側（？）Vector MA(∞) をつくれるというような話があるね。後でどう使うのかわからないけど。それでやっと VAR(p) の自己共分散の話になる。さて、どうやって求めればいいだろう？

どうやってって…そもそも単変量の AR(p) のときはどうしましたっけ。あ、AR(1) の場合は以下の記事で求めていました。

Time Series Analysis：ノート5章最尤推定（その1） - クッキーの日記

定義式 $Y_t = c + \phi Y_{t-1} + \varepsilon_t$ の両辺の分散を取るだけですね。過程が定常である以上 $V(Y_t) = V(Y_{t-1})$ ですから、これについて解けばいいわけです。であれば、VAR(p) の自己共分散も同様に出せるのではないでしょうか？

まあその方向でいいんだけどね。まず 0 次の自己共分散行列がどうなるか具体的にやってみよう。項が p 個あると面倒だから式 (10.1.11) の1次の差分方程式形 $\xi_t = F \xi_{t-1} + v_t$ でやってみよう。これの共分散 $E(\xi_t \xi_t^\top)$ を取るとどうなるだろう？

簡単です。 $E(\xi_t \xi_t^\top) = E \bigl( (F \xi_{t-1} + v_t) (F \xi_{t-1} + v_t)^\top \bigr)$ なので、 $E(\xi_t \xi_t^\top) = F E(\xi_t \xi_t^\top) F^\top + E(v_t v_t^\top)$ と整理して、 $E(\xi_t \xi_t^\top)$ について解けば…あれ、陽に解けない？右から $F^{-1}$ をかけても左から $(F^\top)^{-1}$ をかけても $E(\xi_t \xi_t^\top)$ という行列をかきあらわせませんね…。

うん、そこで vec 演算子を導入しよう。行列を列ごとにばらして1本の縦ベクトルにつなぐ演算子だ。以下の記事（下から3つ目のセリフ）でも行列の微分の定義に利用したよね（以下の記事でもかいているように沖本本の vech 作用素とも似ているけどあちらは対称行列専用なので少し違うよ）。

雑記：積の微分公式の話 - クッキーの日記

この vec 演算子とクロネッカー積（定義はテキスト 732～733 ページをみよう）について成り立つ公式 ${\rm vec}(ABC)= (C^\top \otimes A){\rm vec}(B)$ を用いれば―。

${\rm vec} \bigl(E(\xi_t \xi_t^\top)\bigr) = (I_{(np)^2} - F \otimes F)^{-1} {\rm vec} \bigl( E(v_t v_t^\top) \bigr)$ となるわけですか。 $I_{(np)^2} - F \otimes F$ が正則でないと困りますが、定常 VAR(p) であれば必ず正則になるんですね…証明は面倒なのでしませんが。

では 1 次の自己共分散行列はというと、 $E(\xi_t \xi_{t-1}^\top) = E \bigl( (F \xi_{t-1} + v_t) \xi_{t-1}^\top \bigr) = F E(\xi_{t} \xi_{t}^\top)$ ですから、0 次の自己共分散行列に左から $F$ をかけるだけですか。

ここまで扱ったことをまとめておきましょう。

p 次ベクトル自己回帰過程 VAR(p) は $y_t = c + \Phi_1 y_{t-1} + \cdots + \Phi_p y_{t-p} +\varepsilon_{t}$ と定義される。

係数行列の成分 $\phi_{i,j}^{(\nu)}$ の意味は「 $y_t$ の第 $i$ 成分が $\nu$ ステップ前の自身の第 $j$ 成分にどれだけ依存するか」といえる。
係数行列が定めるある方程式の解がすべて単位円の内側にあるとき VAR(p) は定常であり、定常 VAR(p) は Vector MA(∞) にかき直すことができ、その係数行列は絶対総和可能になる。

q 次ベクトル移動平均過程 Vector MA(q) は $y_t = \mu + \varepsilon_{t} + \Psi_1 \varepsilon_{t-1} + \cdots + \Psi_q \varepsilon_{t-q}$ と定義される。

係数行列の成分 $\psi_{i,j}^{(\nu)}$ の意味は「 $y_t$ の第 $i$ 成分が $\nu$ ステップ前のノイズの第 $j$ 成分にどれだけ依存するか」といえる。
Vector MA(∞) は係数行列が絶対総和可能であるという条件の下で定常であり、その自己共分散行列も絶対総和可能になる。

さらに、ベクトルホワイトノイズが有限な4次モーメントをもつならば Vector MA(∞) の2次モーメントはエルゴード的である。

つづいたらつづく

2021-02-24

Time Series Analysis：ノート10章弱定常ベクトル過程（その1）

本読み

以下の本の10章を読みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

Time Series Analysis

作者:Hamilton, James D.
発売日: 1994/01/11
メディア: ハードカバー

その他の参考文献

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) | 竜義, 沖本 |本 | 通販 | Amazon

関連記事

10章と11章は多変量時系列への拡張みたいだね。例えば「毎年のGNP」と「毎年の国債の金利」を束ねたら多変量時系列になるよね。目次をみるに、10章では単変量時系列のときと同様に改めて多変量時系列のモデルを導入して収束性などの性質を議論して、11章で実際にモデルを使って推定していくのかな。10章冒頭に章の構成について簡単な説明があるね。以下の内容をやっていくみたい。

10.1節ベクトル自己回帰過程の導入
10.2節ベクトル過程の自己共分散と収束
10.3節ベクトル過程の自己共分散生成関数（autocovariance-generating function）

この節は 10.4 節の準備になるみたいだね。

10.4節ベクトル過程のスペクトル
10.5節ベクトル過程の標本平均

この節では命題 7.5 を多変量時系列に拡張するみたい。この結果は後の14章で、自己相関がある場合や不均一分散の場合のOLS推定量を導出するときや、一般化モーメント推定量を考えるときにつかうみたい。あと17章の単位根検定でもつかうって。

ちなみにこの記事のタイトルでは10章のタイトルである Covariance-Stationary Vector Processes を「弱定常ベクトル過程」と訳したけど、これは沖本本の 4.1 節「弱定常ベクトル過程」に倣ったよ。直訳するなら「共分散定常ベクトル過程」だけど、テキスト45ページ（沖本本だと75ページ）にあるように、「弱定常」も「共分散定常」も意味は同じだからね。

はあ…ともかく10章は多変量時系列の導入であって、この章で学んだことを後の章でも利用するのですね？それでその命題 7.5 って何でしたっけ…188ページの以下ですか。

命題 7.5（弱定常過程版の大数の弱法則）

$Y_t$ を $E(Y_t)=\mu, \; E(Y_{t} - \mu)(Y_{t-j} - \mu) = \gamma_j$ であるような弱定常過程とする。但し $\gamma_j$ は絶対総和可能 $\sum_{j=0}^\infty |\gamma_j| < \infty$ とする。このとき標本平均 $\overline{Y}_T =(1/T) \sum_{t=1}^T Y_t$ について以下が成り立つ。

$\overline{Y}_T$ は $\mu$ に2次平均収束する。 $\Rightarrow$ $\overline{Y}_T$ は $\mu$ に確率収束する。
$\lim_{T \to \infty} \bigl[ T E(\overline{Y}_T - \mu)^2 \bigr] = \sum_{j = -\infty}^\infty \gamma_j$

これは以下の通常版の大数の弱法則（183ページ）を弱定常過程版にしたものでしたね。

命題（通常版の大数の弱法則）

$Y_t$ を $E(Y_t)=\mu, \; E(Y_{t} - \mu)^2 = \sigma^2 < \infty$ であるような i.i.d.過程とする。このとき標本平均 $\overline{Y}_T =(1/T) \sum_{t=1}^T Y_t$ について以下が成り立つ。

$\overline{Y}_T$ は $\mu$ に2次平均収束する。 $\Rightarrow$ $\overline{Y}_T$ は $\mu$ に確率収束する。

標本サイズを大きくしたときに真のパラメータに確率収束するような推定量を一致推定量とよびますから、これらは「標本平均は母平均の一致推定量である」といっているに他ならないのですね。…それで、多変量時系列版ではどうなるのかを先に覗いてみましょう。10.5節の279ページの最下部ですね。以下の $y_t$ や $\mu$ は太字にしませんが $n$ 次元のベクトルとしていますので注意してください。 $\Gamma_\nu$ は $n \times n$ 次元の自己共分散行列です。

命題 10.5（弱定常ベクトル過程版の大数の弱法則）

$y_t$ を $E(y_t)=\mu, \; E(y_{t} - \mu)(y_{t-\nu} - \mu)^\top = \Gamma_\nu$ であるような弱定常ベクトル過程とする。但し $\Gamma_\nu$ は成分ごとに絶対総和可能 $\sum_{\nu=0}^\infty |\gamma_{i,j}^{(\nu)}| < \infty$ とする。このとき標本平均 $\overline{y}_T =(1/T) \sum_{t=1}^T y_t$ について以下が成り立つ。

$\overline{y}_T$ は $\mu$ に成分ごとに2次平均収束する。 $\Rightarrow$ $\overline{y}_T$ は $\mu$ に成分ごとに確率収束する。
$\lim_{T \to \infty} \bigl[ T E(\overline{y}_T - \mu)(\overline{y}_T - \mu)^\top \bigr] = \sum_{\nu = -\infty}^\infty \Gamma_\nu$

こうして見比べると命題 7.5 と似ていますね。多変量になったといっても様変わりしてしまったという感じにはみえないです。しかし、この命題 10.5 が何になるのでしょうか？

何って、標本平均がどんな性質をもっているのか押さえておかないと、それをつかった推定や検定がどのような性質をもつのかわからないからね？後の章で扱うのかと思ったけど、10.5節の続きにも色々な推定量が紹介されているからそれをみればわかるんじゃないかな。…ともかく10.1節の内容に入っていこう。早速257ページで p 次のベクトル自己回帰過程 VAR(p) を以下のように定義しているね。

$y_t = c + \Phi_1 y_{t-1} + \cdots + \Phi_p y_{t-p} +\varepsilon_{t} \tag{10.1.4}$ $y_t, c, \varepsilon_{t}$ はもはや $n$ 次元のベクトルだね。 $\Phi_\nu$ は $n \times n$ 次元の係数行列だね。

えっと、自己回帰過程 AR(p) では係数 $\phi_j$ はスカラーでしたよね。それがいまや行列になったのですね。…しかし、その行列の各成分は何を意味するのでしょうか。その VAR(p) の第1成分をかき下してみましょう。ここで行列 $\Phi_\nu$ の $i$ 行 $j$ 列の成分を $\phi_{i,j}^{(\nu)}$ とかき、ベクトル $y_t$ の $i$ 番目の成分を $y_{t,i}$ とかきます（ベクトルの添え字をテキストと逆にしたので注意してください）。

$\begin{split} y_{t,1} = c_1 &+ \phi_{1,1}^{(1)} y_{t-1,1} + \phi_{1,2}^{(1)} y_{t-1,2} + \cdots + \phi_{1,n}^{(1)} y_{t-1,n} \\ &+ \phi_{1,1}^{(2)} y_{t-2,1} + \phi_{1,2}^{(2)} y_{t-2,2} + \cdots + \phi_{1,n}^{(2)} y_{t-2,n} + \cdots \\ &+ \phi_{1,1}^{(p)} y_{t-p,1} + \phi_{1,2}^{(p)} y_{t-p,2} + \cdots + \phi_{1,n}^{(p)} y_{t-p,n} +\varepsilon_{t,1} \end{split} \tag{10.1.7}$ こうですね。となると、 $\phi_{i,j}^{(\nu)}$ の意味は「 $y_t$ の第 $i$ 成分が $\nu$ ステップ前の第 $j$ 成分にどれだけ依存するか」といえますね。

そうだね。あと $\varepsilon_{t}$ もいまやホワイトノイズからベクトルホワイトノイズになっているからね。つまり、 $\varepsilon_{t}$ は確率ベクトルであって、任意の $t$ で平均ベクトルが $E(\varepsilon_{t}) = 0$ であって、自己共分散行列 $E(\varepsilon_{t} \varepsilon_{t'}^\top)$ は $t = t'$ のときのみ $n \times n$ 正定値行列 $\Omega$ であって、 $t \neq t'$ のときは零行列だ。ちなみに沖本本76ページの記述だけど「 $\Omega$ は対角行列である必要はない」よ。例えば、日々の気温とアイスクリームの売り上げを2変量時系列とみなして VAR(p) でモデリングするとしたら、 $\Omega$ はきっと正の非対角成分をもつんじゃないかな。だって、ある日に偶発的に気温が高くなったとしたら、その日はアイスクリームも想定より売れそうだもんね。そこは相関があっていい。でも、ある日に偶発的に気温が高くなったのがその次の日以降の気温／アイスクリームの売り上げに影響するのは駄目。 $t \neq t'$ のときは零行列だから。日付をまたいだ影響は係数行列 $\Phi_\nu$ で表現しないといけない。

なるほど。異なる日のノイズどうしは無相関だが同じ日のノイズの成分どうしは相関があってもいいんですね。VAR(p) がどのようなモデルなのかは理解した気がします。…しかし、AR(p) がそうであったように VAR(p) も $\Phi_\nu$ に何か条件を課さないと定常にはならないのですよね？復習すると、過程が（弱）定常であることの定義は以下でした。平均が時刻によらず、自己共分散も時刻によらず時間差だけに依存するということですね。

定義（単変量時系列の弱定常性）

任意の $t$ と $j$ に対して $E(Y_t) = \mu, \; E(Y_t - \mu)(Y_{t-j} - \mu) = \gamma_j$ が成立するとき、過程 $Y_t$ は弱定常であるという。

以下、単に定常といった場合弱定常を指すことにします。AR(p) の定常条件は以下でした。

命題（AR(p) の定常条件）

AR(p) $Y_t = c + \phi_1 Y_{t-1} + \cdots + \phi_p Y_{t-p} +\varepsilon_{t}$ の定常条件は以下である（どちらも同じ）。

方程式 $\lambda^p - \phi_1 \lambda^{p-1} - \cdots - \phi_p = 0$ の解がすべて単位円より内側にある。
方程式 $1 - \phi_1 z - \cdots - \phi_p z^p = 0$ の解がすべて単位円より外側にある。

なぜこのような条件になるのかはテキスト7〜13ページですね。AR(p) が定常であると仮定すると、その平均 $\mu$ からの差分を取って、ベクトルに束ねて、式 (1.2.5) の $\xi_t = F \xi_{t-1} + v_t$ の形にすることができるはずです（具体的にかき下すと以下）。 $\displaystyle \left(\begin{array}{c} y_t - \mu \\ y_{t-1} - \mu \\ \vdots \\ y_{t-p+1} - \mu \end{array}\right) = \left(\begin{array}{ccccc} \phi_1 & \phi_2 & \cdots & \phi_{p-1} & \phi_p \\ 1 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \end{array}\right) \left(\begin{array}{c} y_{t-1} - \mu \\ y_{t-2} - \mu \\ \vdots \\ y_{t-p} - \mu \end{array}\right) + \left(\begin{array}{c} \varepsilon_t \\ 0 \\ \vdots \\ 0 \end{array}\right) \tag{1.2.5}$ この $F$ を対角化 $F=T \Lambda T^{-1}$ すると $\Lambda$ は対角成分に $F$ の固有値が並んだ対角行列になりますが、この固有値の中に絶対値が1より大きいものがあったら、どこかの時刻で発生した $\mu$ からの差分が爆発していってしまいますよね。それだと自己共分散が時刻によらないことに矛盾します。逆にすべての固有値の絶対値が1未満ならば、どこかの時刻で発生した $\mu$ からの差分はいつしか消えてなくなるので、この過程の自己共分散は時刻に依存しません。 $F$ の固有値 $\lambda$ は方程式 $\lambda^p - \phi_1 \lambda^{p-1} - \cdots - \phi_p = 0$ の解になります（命題 1.1）。なので AR(p) の定常条件は上のようになるわけです。

…単変量の AR(p) のときはこうでしたが、多変量の VAR(p) になると定常条件はどうなるのでしょうか？

先に多変量時系列の場合の弱定常性の定義を一応かいておくよ。単変量のときと同様だけど。

定義（多変量時系列の弱定常性）

任意の $t$ と $\nu$ に対して $E(y_t) = \mu, \; E(y_t - \mu)(y_{t-\nu} - \mu)^\top = \Gamma_\nu$ が成立するとき、過程 $y_t$ は弱定常であるという。

それで、VAR(p) でも AR(p) のときとやることは同じだよ。VAR(p) をベクトルに束ねて $\xi_t = F \xi_{t-1} + v_t$ の形にする。式 (10.1.11) だね。

またしてもベクトルに束ねるのですか。…いえでも、今回は元々ベクトルであるのをさらにベクトルに束ねるということになりますね？？ $\xi_t = F \xi_{t-1} + v_t$ をきちんとかき下してみましょう。この $F$ は $np \times np$ 行列なのですね…。

$\displaystyle \left(\begin{array}{c} y_t - \mu \\ y_{t-1} - \mu \\ \vdots \\ y_{t-p+1} - \mu \end{array}\right) = \left(\begin{array}{ccccc} \Phi_1 & \Phi_2 & \cdots & \Phi_{p-1} & \Phi_p \\ I_n & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_n & 0 \end{array}\right) \left(\begin{array}{c} y_{t-1} - \mu \\ y_{t-2} - \mu \\ \vdots \\ y_{t-p} - \mu \end{array}\right) + \left(\begin{array}{c} \varepsilon_t \\ 0 \\ \vdots \\ 0 \end{array}\right) \tag{10.1.11}$ まあでも、今回も $F$ のすべての固有値の絶対値が1未満であるべきという条件は変わらないですね。多変量時系列のどれか1つの成分でも爆発したら定常でなくなってしまいますから。そうすると、1章のときと同様の操作をして、結局以下のようになりますね。

命題 10.1（VAR(p) の定常条件）

VAR(p) $y_t = c + \Phi_1 y_{t-1} + \cdots + \Phi_p y_{t-p} +\varepsilon_{t}$ の定常条件は以下である。

方程式 $\bigl| \lambda^p I_n - \lambda^{p-1} \Phi_1 - \cdots - \Phi_p \bigr| = 0$ の解がすべて単位円より内側にある。

この縦棒は行列式の意味である。つまり、これは $\lambda$ の $np$ 次方程式である。

10.1節の続きには、「Vector MA(∞) 表現」というのが出てきますね。AR(p) は定常であれば MA(∞) にかき直すことができましたが、VAR(p) も定常であれば Vector MA(∞) にかき直せるということでしょうか。

そうだね。 $\xi_t = F \xi_{t-1} + v_t$ を繰り返し適用すれば、

$\xi_{t} = v_{t} + F v_{t-1} + F^2 v_{t-2} + F^3 v_{t-3} + \cdots$ となって、この両辺のベクトルの最初の $n$ 個の成分を取れば、 $y_{t} = \mu + \varepsilon_{t} + F_{1,1} \varepsilon_{t-1} + F_{1,1}^{(2)} \varepsilon_{t-2} + F_{1,1}^{(3)} \varepsilon_{t-3} + \cdots$ となるからね。これは Vector MA(∞) だ。ところで、 $F_{1,1}^{(\nu)}$ は $F^{\nu}$ の左上 $n \times n$ ブロックを指すよ。ところで、正則な $n \times n$ 行列 $H$ があったとき、以下のように $H^{-1} H$ を挟むことは差し支えないよね。 $y_{t} = \mu + H^{-1} H \varepsilon_{t} + F_{1,1} H^{-1} H \varepsilon_{t-1} + F_{1,1}^{(2)} H^{-1} H \varepsilon_{t-2} + F_{1,1}^{(3)} H^{-1} H \varepsilon_{t-3} + \cdots$

差支えはありませんが、それが何ですか？

いまベクトルホワイトノイズは $\varepsilon_t$ だけど、 $u_t = H \varepsilon_t$ というように変換されたベクトルホワイトノイズで考えてもいいってことみたい。特に、いま $\varepsilon_t$ の分散共分散行列は $\Omega$ だけど、 $\Omega$ を対角化 $H\Omega H^\top = D$ するような $H$ を選んでベクトルホワイトノイズを $u_t = H \varepsilon_t$ と変換すれば、 $u_t$ の成分どうしを無相関にできる。

ああ、 $\varepsilon_t$ の確率密度関数は $f(\varepsilon_t) \propto \exp(-0.5 \varepsilon_t^\top \Omega^{-1} \varepsilon_t)$ ですから、 $u_t = H \varepsilon_t$ と変換したときの確率密度関数は $f(u_t) \propto \exp(-0.5 u_t^\top (H^{-1})^\top \Omega^{-1} H^{-1} u_t) = \exp(-0.5 u_t^\top (H\Omega H^\top)^{-1} u_t)$ となって、分散共分散行列が対角行列になり、成分ごとに無相関になりますね。

でもその場合 Vector MA(∞) は $y_{t} = \mu + H^{-1} u_t + \cdots$ となっちゃって $u_t$ の項に係数行列がかかっちゃうから、それを許容しないなら成分ごとに無相関にはできないんだけどね。というか Vector MA(∞) の定義がすぐ後に出てくる式 10.2.3 だと思うんだけど、 $\varepsilon_t$ に係数行列はかかっていないから、ノイズを変換しちゃうとやっぱり厳密には Vector MA(∞) ではないね。

続く 10.2 節は、まずベクトル過程の自己共分散行列の定義かな。つまり、定常ベクトル過程 $y_t$ の $\nu$ 次の自己共分散行列は $\Gamma_{\nu} = E \bigl[ ({y}_t - \mu)({y}_{t - \nu} - \mu)^\top \bigr]$ だ。単変量のときの自己共分散と似ているね。ただ注意してほしいのは、 $\Gamma_{\nu}$ と $\Gamma_{-\nu}$ が同じになるとは限らない。成り立つのは $\Gamma_{\nu}^\top = \Gamma_{-\nu}$ になる。

えっ、何故そのような違いが。

もはや積が交換しないしね。 $({y}_t - \mu)({y}_{t - \nu} - \mu)^\top$ と $({y}_{t-\nu} - \mu)({y}_{t} - \mu)^\top$ って一般に等しくないよね。

ああ確かに… $\Gamma_\nu$ の1行目は「 $y_{t,1}$ と $y_{t-\nu,1}, \, y_{t-\nu,2}, \cdots, y_{t-\nu,n}$ 」との共分散ですが、 $\Gamma_{-\nu}$ の1行目は「 $y_{t-\nu,1}$ と $y_{t,1}, \, y_{t,2}, \cdots, y_{t,n}$ 」との共分散ですから、意味が違いますね…。

その2につづく

2021-02-17

雑記：単語分散表現の話

雑記

word2vecとGloVeが、前者が predicting で後者が counting といわれたり、結果として得られる「 $v$ _女王 $\fallingdotseq v$ _王 $+ v$ _女性 $- v$ _男性」という関係式が直感的でめでたしめでたしとなったりしていると思うんですが、どちらも predict しているのではないのかとか、何が直感的なのかとかわからなかったので、word2vecとGloVeが何を目指しているかのメモをかきました。

モデルの定式化は全面的に参考文献1. に依っていますが、記事の最初の方と最後の方には私の適当な解釈を多分に含みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

ゴールとして、「もしword2vecが単語類似度タスクに強くGloVeがニュース分類タスクに強い（要出典）のだとしたら、後者は共起行列をつくってから学習し前者はそうでないため、前者は特定の文脈にフィットする解を目指しやすいが後者はあくまで全体の平均を目指し、それゆえに前者は単語類似度タスク（特定の文脈での意味）に強く後者がニュース分類タスク（ニュースを構成する単語全体の意味）に強いのではないか」というような考察を適当ではなくきちんとできるようになりたかったのですが、そこまでいきませんでした。また参考文献1. の 2-7 節に、「単語の分散表現の性能差は各モデルの理論的な側面よりも、実装上の細かいトリックや実験設定に左右されるとの指摘がある．」との記述があります。

参考文献

岡崎直観. 言語処理における分散表現学習のフロンティア（＜特集＞ニューラルネットワーク研究のフロンティア）. 人工知能, 31(2), 189-201, 2016. 言語処理における分散表現学習のフロンティア(<特集>ニューラルネットワーク研究のフロンティア)

人工知能学会の学会誌の2016年3月号の記事です。

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., Dean, J. Distributed Representations of Words and Phrases and their Compositionality, Proc. of NIPS, pp. 3111-3119, 2013. [1310.4546] Distributed Representations of Words and Phrases and their Compositionality

word2vecの原論文です。

https://code.google.com/archive/p/word2vec/

word2vecの実装があり、architecture: skip-gram (slower, better for infrequent words) vs CBOW (fast) などのメモがあります。

Pennington, J., Socher, R., Manning, C.. Glove: Global vectors for word representation, Proc. of EMNLP, pp. 1532-1543, 2014. GloVe: Global Vectors for Word Representation - ACL Anthology

GloVeの原論文です。

https://nbviewer.jupyter.org/github/DSKSD/DeepNLP-models-Pytorch/blob/master/notebooks/03.GloVe.ipynb

GloVeの実装です。

まとめ（文字の定義は後述）

skip-gram も GloVe も、結局、単語 $c$ の周辺（前後 $\delta$ 語など、適当に決める）に出現する単語 $w$ の分布 $p(w|c)$ を、内積のエクスポネンシャルによるモデル $q(w|c) = C_c \tilde{C}_w \exp(v_c^\top \tilde{v}_{w})$ でフィッティングすることを通して単語 $c$ のベクトル表現 $v_c$ を得ようとするのは共通している。

$\tilde{C}_w = 1$ のときは $q(w|c) = {\rm softmax}(v_c^\top \tilde{v}_{w})$ に他ならない。 $C_c$ は規格化定数である。
$q(w|c_a)$ と $q(w|c_b)$ の比に興味があるときは $\tilde{C}_w > 0$ があってもよい（比をとると消える）。

但し、分布間の距離の指標は様々であるし、そもそも語彙数が膨大であるためにこの分布の規格化定数を直接計算するのも現実的ではない。skip-gram と GloVe は何を最小化しようとしてどのように規格化を回避するかが異なっている。

skip-gram は $q(w|c) = {\rm softmax}(v_c^\top \tilde{v}_{w})$ とし、学習コーパス内に出現するすべての「単語 $c$ - その周辺の単語 $w$ 」の組の条件付き確率 $q(w|c)$ の対数の和 $\sum_{t=1}^T \sum_{c \in C_{w_t}} \log q(w_t|c)$ を最大化するように（∴ 交差エントロピーの重み付き和 $- \sum_{c \in V} \#(c,\cdot) \sum_{w \in V} p(w|c) \log q(w|c)$ を最小化するように）学習することを目指す。が、規格化の計算が難しいので ${\rm sigmoid}(v_c^\top \tilde{v}_{w})$ による2値分類タスクにしてしまう（正例1個につき負例用の周辺単語を $K$ 個サンプリングする）。

CBOW（その名の通り周辺の単語を先に「カバン」に入れて＝足してしまう）はこの最適化をさらに簡略化したものとも捉えられる。

GloVe は $p(w|c) = \#(c, w) / \#(c, \cdot )$ であることに着目して、「 $p(w|c)$ を $q(w|c) = C_c \tilde{C}_w \exp(v_c^\top \tilde{v}_{w})$ でフィッティングするタスク」を、「 $\log \#(c, w)$ を $v_c^\top \tilde{v}_w + b_c + \tilde{b}_w$ でフィッティングするタスク」に読み替える。損失は2乗誤差を採用するが、あまり発生しない「単語 $c$ - その周辺の単語 $w$ 」の組に対しては重みを小さくするようにする。

そのため、予め $\#(c, w)$ のテーブルを用意しておくことになる。

いずれにせよ、skip-gram や GloVe で得たベクトルは「内積が対数確率をオフセットしたもの」という性質をもっている。内積は分配則が成り立つ（和の内積は内積の和）ので、 $v_a + v_b$ は「周辺の単語の対数確率が単語 $a$ の周辺の対数確率と単語 $b$ の周辺の対数確率の和になるような仮想的な単語のベクトル」と捉えられる。となると、 $v$ _王 $+ v$ _女性 $- v$ _男性というベクトルをもつ仮想的な単語が考えられるが、 $v$ _女王がそれに近かったという事実は、「女王」の周りの分布がそのように「王」「女性」「男性」の分布で特徴付けられるということに他ならない。

まとめ（文字の定義は後述）
word2vecのモデル
- skip-gram
- CBOW（continuous bag-of-words）
GloVeのモデル
得られたベクトル表現の性質

word2vecのモデル

学習コーパスを単語列 $w_1, w_2, \cdots, w_T$ とする。
単語 $w_t$ を中心語とした前後 $\delta$ 語の文脈窓を $C_{w_t} = (w_{t-\delta}, \cdots, w_{t-1}, w_{t+1}, \cdots, w_{t+\delta})$ とする。

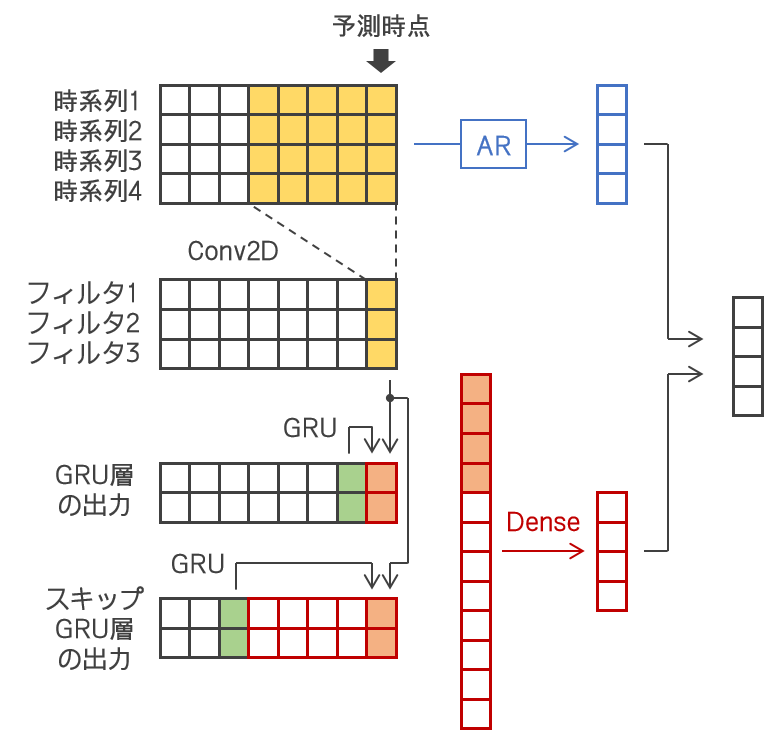
word2vecでは、文脈窓 $C$ を与えたときの中心語の確率分布 $p(w|C)$ を、 $C$ 内の単語のベクトルを用いてモデリングすることを通して、単語のベクトル表現を獲得する。つまり、長さ $2 \delta$ の単語列を与えたときに、それらの単語のベクトル表現を用いてどんな単語がその中央にはまりそうかの分布を出すことを目指すのだが、 $2 \delta$ 個の単語の情報をどう集約するかで流派が分かれる（下図）。
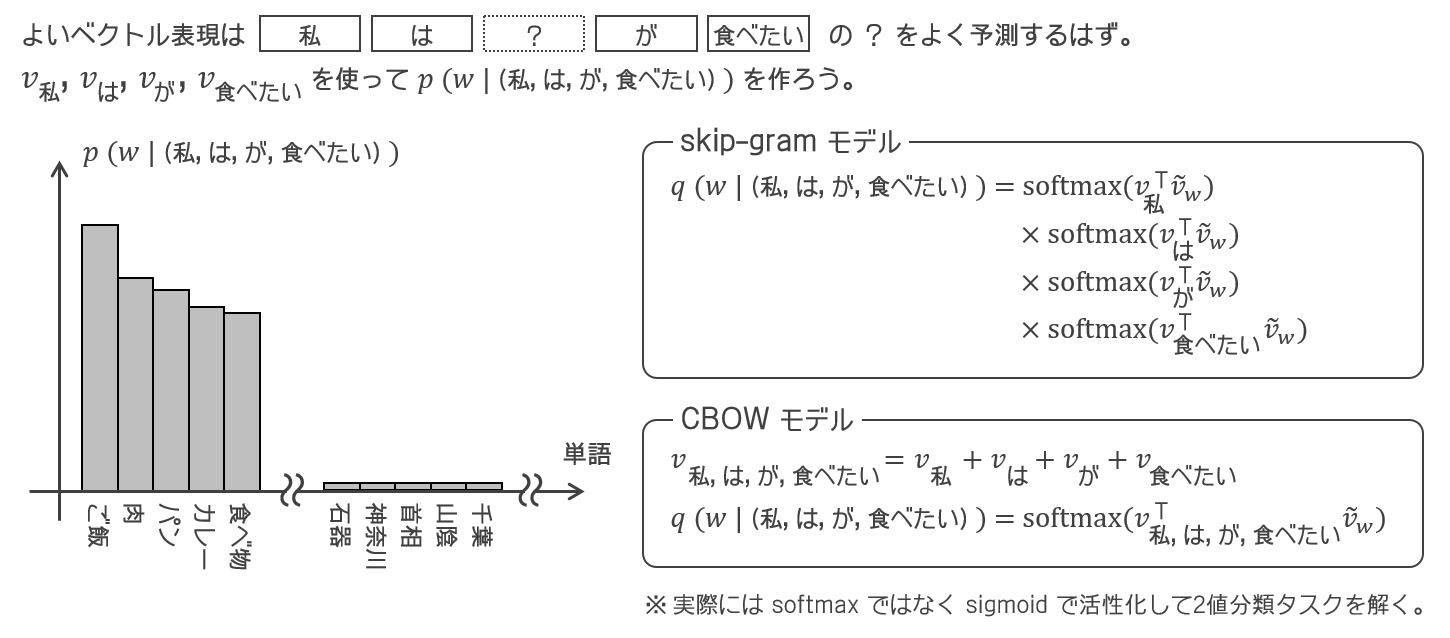
f:id:cookie-box:20210217225124p:plain

skip-gramでは $p(w|C)$ を $\prod_{c \in C} {\rm softmax}(v_c^\top \tilde{v}_{w})$ でモデリングする。
つまり、「文脈窓の中心にどんな単語がきそうか」を、文脈窓内の各単語の「この単語がいる文脈窓の中心にどんな単語がきそうか」の積で表現する（先に各単語からの確率を出して積をとって集約する派）。
CBOWでは $p(w|C)$ を ${\rm softmax} \left( \left( \sum_{c \in C}v_c \right)^\top \tilde{v}_{w} \right)$ でモデリングする。
つまり、「文脈窓の中心にどんな単語がきそうか」を、文脈窓内の全単語のベクトルの和で表現する（先に全単語のベクトルを和に集約してから確率を出す派）。

但し実際にはソフトマックスではなくシグモイドで活性化し、サンプリングした負例との2値分類を学習する。

skip-gram

skip-gramでは $p(w|C) = \prod_{c \in C} p(w|c)$ と考える。 $p(w|c)$ はいわば「単語 $c$ を与えたときに単語 $w$ が単語 $c$ のいる文脈窓の中心語である確率」になる。この $p(w|c)$ をモデル $q(w|c) = {\rm softmax}(v_c^\top \tilde{v}_{w})$ でフィッティングする。ただし、 $v_c$ は単語 $c$ の文脈語としてのベクトル、 $\tilde{v}_{w}$ は単語 $w$ の中心語としてのベクトルであり、全単語にこれらのベクトルをどう用意すべきかがフィッティング対象となる。損失関数は以下とする（学習コーパス内のすべての中心語-文脈語の組の確率の積を最大化する＝対数確率の和を最小化する）。
$\displaystyle \mathcal{L}^{\rm SG} = \sum_{t=1}^T \sum_{c \in C_{w_t}} \log q(w_t | c) = \sum_{t=1}^T \sum_{c \in C_{w_t}} \log {\rm softmax}(v_c^\top \tilde{v}_{w_t}) = \sum_{t=1}^T \sum_{c \in C_{w_t}} \log \frac{\exp (v_c^\top \tilde{v}_{w_t})}{ \sum_{w' \in V} \exp (v_c^\top \tilde{v}_{w'})}$ 但し実際には全単語 $V$ 上でソフトマックスをとることは難しいので損失関数を少し変更する。「文脈語 $c$ から中心語 $w$ を当てる $\# V$ 値分類タスク」ではなく「文脈語 $c$ と中心語 $w$ が正しい文脈語と中心語の組かどうか当てる $2$ 値分類タスク」と考えることにして、活性化関数をソフトマックスからシグモイドに取り換える。このタスク設定にすると負例が必要になるので、中心語-文脈語の組1つにつき、負例のための中心語 $w^{(k)}$ を $K$ 回サンプリングする（単語のユニグラム分布からサンプリングする）。
$\displaystyle \mathcal{L}^{\rm SG} = \sum_{t=1}^T \sum_{c \in C_{w_t}} \left( \log \frac{\exp (v_c^\top \tilde{v}_{w_t})}{1 + \exp (v_c^\top \tilde{v}_{w_t})} + \sum_{k=1}^K \log \left( 1 - \frac{\exp (v_c^\top \tilde{v}_{w^{(k)}})}{1 + \exp (v_c^\top \tilde{v}_{w^{(k)}})} \right) \right)$ この損失関数を最小化するように学習し、各単語の文脈語としてのベクトル $v_c$ をその単語のベクトル表現とする。

CBOW（continuous bag-of-words）

文脈窓 $C$ に対して、文脈窓内の単語の文脈語としてのベクトルの和を $v_C = \sum_{c \in C} v_c$ とする。CBOWでは $p(w|C)={\rm softmax}(v_C^\top \tilde{v}_{w})$ と考える。損失関数は以下となる。 $\displaystyle \mathcal{L}^{\rm CBOW} = \sum_{t=1}^T \log q(w_t | C_{w_t}) = \sum_{t=1}^T \log {\rm softmax}(v_{C_{w_t}}^\top \tilde{v}_{w_t}) = \sum_{t=1}^T \log \frac{\exp (v_{C_{w_t}}^\top \tilde{v}_{w_t})}{ \sum_{w' \in V} \exp (v_{C_{w_t}}^\top \tilde{v}_{w'})}$ 但し実際には全単語 $V$ 上でソフトマックスをとることは難しいので skip-gram 同様に損失関数を変更する。 $\displaystyle \mathcal{L}^{\rm CBOW} = \sum_{t=1}^T \left( \log \frac{\exp (v_{C_{w_t}}^\top \tilde{v}_{w_t})}{1 + \exp (v_{C_{w_t}}^\top \tilde{v}_{w_t})} + \sum_{k=1}^K \log \left( 1 - \frac{\exp (v_{C_{w_t}}^\top \tilde{v}_{w^{(k)}})}{1 + \exp (v_{C_{w_t}}^\top \tilde{v}_{w^{(k)}})} \right) \right)$

GloVeのモデル

GloVeでは、2単語のベクトルの差でそれぞれの単語の周辺に出現する単語の確率分布の比をモデリングすることを通して、単語のベクトル表現を獲得する。但し、「周辺に出現する単語のベクトルと内積をとった上でエクスポネンシャルをとる」というモデルにしたため、結局、個々の単語の確率分布をモデリングすることになっている。 f:id:cookie-box:20210218003922p:plain

具体的に、

単語 $i$ の周辺に単語 $j$ が出現した回数を $\#(i, j)$ とする。
単語 $i$ の周辺に任意の単語が出現した回数を $\#(i, \cdot )$ とする。
単語 $i$ の周辺に単語 $j$ が出現する確率は $p(j|i) = \#(i, j) / \#(i, \cdot )$ となる。

が、確率分布 $p(j|i)$ そのものは、どんな単語の周辺にもよく出現するような単語 $j$ で大きくなるため、単語 $i$ のよい特徴になっていない。それよりも、他の単語 $k$ の分布との比を取った $p(j|i)/p(j|k)$ の方が単語 $i$ の単語 $k$ との関係のよい特徴になっている。ので、確率分布の比 $p(j|i)/p(j|k)$ を $F(v_i, v_k, \tilde{v}_j)$ でモデリングすることを目指す。ここで、 $F$ の関数形に以下を仮定する。

$v_i, v_k$ に依存する項は $v_i, v_k$ の差 $v_i - v_k$ にのみ依存する。
$v_i - v_k$ をスカラーに変換するにあたり $\tilde{v}_j$ との内積 $(v_i - v_k)^\top \tilde{v}_j$ をとる。
$(v_i - v_k)^\top \tilde{v}_j$ を確率分布の比に変換するにあたり、和を変換したものが変換したものの積になるように $\exp$ を採用する（同じ単語どうしの確率分布の比は常に1にならなければならない）。

よって、 $F(v_i, v_k, \tilde{v}_j) = \exp \bigl( (v_i - v_k)^\top \tilde{v}_j \bigr)$ となるが、そうなると $p(j|i)/p(j|k)$ を $\exp(v_i^\top \tilde{v}_j)/\exp(v_k^\top \tilde{v}_j)$ でモデリングすることになるので、 $p(j|i)$ を $\tilde{C}_j \exp(v_i^\top \tilde{v}_j)$ でモデリングすることと同じである（ $\tilde{C}_j$ は $j$ にのみ依存する係数）。さらに、 $p(j|i) = \#(i, j) / \#(i, \cdot )$ を利用すると、 $\log \#(i, j)$ を $v_i^\top \tilde{v}_j + b_i + \tilde{b}_j$ でモデリングすることになる。損失は2乗誤差を採用する。 $\displaystyle \mathcal{L}^{\rm GloVe} = \sum_{i=1}^{|V|} \sum_{j=1}^{|C|} f(\#(i,j)) \left( v_i^\top \tilde{v}_j + b_i + \tilde{b}_j - \log \#(i, j) \right)^2$ 但し、 $f(\#(i,j))$ は共起頻度が小さいペアの重みを小さくするための因子で、例えば以下（共起頻度が100回未満のペアの重みを徐々に軽くする例）が用いられる。 $\displaystyle f(x) = \begin{cases} (x / 100)^{0.75} & (x < 100) \\ 1 & ({\rm otherwise}) \end{cases}$

得られたベクトル表現の性質

これらの手法で得られた単語のベクトル表現は、モデルより、別の単語のベクトル表現との内積が意味をもつ（対数確率をオフセットしたものになる）。もし $C_a \fallingdotseq C_b$ であれば、

$v_a^\top \tilde{v}_x$ が、単語 $x$ が単語 $a$ の周辺にいそうな度合いになる。
$v_b^\top \tilde{v}_x$ が、単語 $x$ が単語 $b$ の周辺にいそうな度合いになる。
$v_b^\top \tilde{v}_x - v_a^\top \tilde{v}_x = (v_b - v_a)^\top \tilde{v}_x$ は、それらの差になる。

$(v$ _女性 $- v$ _男性 $)^\top \tilde{v}$ _スカートは、正になりそう（※ 適当な例）。
$(v$ _女性 $- v$ _男性 $)^\top \tilde{v}$ _ズボンは、負になりそう（※ 適当な例）。

$v_{a'}^\top \tilde{v}_x + v_b^\top \tilde{v}_x - v_a^\top \tilde{v}_x = (v_{a'} + v_b - v_a)^\top \tilde{v}_x$ は、単語 $x$ が単語 $a'$ の周辺にいそうな度合いに先の差を足したものになる。

$(v$ _王 $+ v$ _女性 $- v$ _男性 $)^\top \tilde{v}$ _スカートは、「王」の文脈に「スカート」がいそうな度合いを大きくしたもの。
$(v$ _王 $+ v$ _女性 $- v$ _男性 $)^\top \tilde{v}$ _ズボンは、「王」の文脈に「ズボン」がいそうな度合いを小さくしたもの。
同様に、任意の単語 $x$ について、 $(v$ _王 $+ v$ _女性 $- v$ _男性 $)^\top \tilde{v}_x$ は、「王」の周辺に $x$ がいそうな度合いに、「女性」の周辺に $x$ がいそうな度合いを足して、「男性」の周辺に $x$ がいそうな度合いを引いたもの。

word2vecで（GloVeでも） $v$ _女王 $\fallingdotseq v$ _王 $+ v$ _女性 $- v$ _男性となることがよく知られているが、それは、任意の単語 $x$ について、「女王」の周辺に $x$ がいそうな度合いが、「王」の周辺に $x$ がいそうな度合いに「女性」の周辺に $x$ がいそうな度合いを足して「男性」の周辺に $x$ がいそうな度合いを引いたものに近くなっていることを示唆しているのに他ならない。

2021-02-11

論文読みメモ： Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

論文読み

2021-02-14 3枚目の絵を修正しました。

以下の論文を読みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

Haoyi Zhou, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, Wancai Zhang. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. arXiv preprint arXiv:2012.07436, 2020.
[2012.07436] Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
GitHub - zhouhaoyi/Informer2020: The GitHub repository for the paper "Informer" accepted by AAAI 2021.

まとめ

遠い過去のステップも直接「注意」しにいける Transformer は時系列データの長期予測に有用と考えられるが、長い系列を Transformer に流すには以下の難点がある。

セルフアテンションする以上、系列長 $L$ に対して $\mathcal{O}(L^2)$ の計算量がかかる。
セルフアテンション層を積み重ねる原理上、推論時に膨大なメモリを要する。
推論に時間がかかる（再帰的にデコードするため）（誤差の蓄積の問題もある）。

そこで提案モデル「Informer」ではこれらの難点を以下のように克服した。

「ProbSparse」というセルフアテンション手法で特徴抽出性能を維持しつつ計算量を $\mathcal{O}(L \log L)$ に抑えた。

方針として、 ${\rm Softmax}(QK^\top /\sqrt{d}) \in \mathbb{R}^{L \times L}$ の各行のうち一様分布からの逸脱度が大きい行（＝重要な「注意」を含んでいる見込みが高い）だけを残し他の行は捨てる。サンプリングによって逸脱度を見積もる。

セルフアテンション層を出る度に Conv1D + MaxPool1D して系列の長さを半分にしていくことでメモリ使用量を抑えた（セルフアテンション蒸留）。
再帰的にデコードするのではなく一気にデコードすることで推論速度を大幅に向上させた（生成的デコーダ）。

この「Informer」はデータセット「Electricity Transformer Temperature（著者による変電所の変圧器の油温データ）」、「Electricity Consuming Load」、「Weather」を使用したさまざまな長期予測タスク（単/多変量予測 × 24～960ステップ先予測）のほとんどで既存手法（ARIMA、Prophet、LSTMa、LSTnet、DeepAR）を上回る精度を示した。また、

「ProbSparse」によるセルフアテンションの有効性の検証として、「通常のセルフアテンション」「Reformer のセルフアテンション」「LogSparse Transformer のセルフアテンション」に置き換えたモデルとも比較されたが、やはりほとんどのタスクでこれらのモデルよりも高い精度を示した。特に、通常のセルフアテンション（計算量大）よりもむしろ精度がよいケースが多かった（＝「ProbSparse」による取捨選択が功を奏した）。
セルフアテンション蒸留の有効性の検証として、セルフアテンション蒸留しないモデル構造とも比較されたが、入力系列の長さが同じであれば蒸留しないモデルの方が精度が出るが、蒸留しないモデルでは入力系列を長くするとアウトオブメモリーになるので、結局セルフアテンション蒸留をした方がよかった。
生成的デコーダの検証として再帰的にデコードするモデルとも比較されたが、再帰的にデコードするモデルでは誤差が大きすぎた。

所感

提案した3コンポーネント全ての有効性を示している。
セルフアテンションの計算量の削減の仕方が、先行研究の LogSparse Transformer のように「近くは綿密に計算するが遠くにいくほどどんどんとばす」という幾分アドホックなものではなく、積極的に何かを強く注意している行を優先して残そうとするものになっている。その有効性は通常のセルフアテンションの予測性能を上回っていることで示されている。
NeurIPS2020 の Adversarial Sparse Transformer は Transformer を敵対的に学習することで長期予測における誤差の蓄積を回避したが、そもそも再帰的に予測したいという要請がなければ Informer のように一度に予測すればよいと考えられる。

導入
モデル
検証データと比較手法

導入

この「Informer」は「Transformer による時系列の長期予測」とのことですが、つい最近も「Transformer による時系列の長期予測」をみた気が…以下の「AST（Adversarial Sparse Transformer）」ですね。

NeurIPS2020読みメモ： Adversarial Sparse Transformer for Time Series Forecasting

「AST」が工夫した点は α-entmax を用いてアテンションを疎にし重要な情報をこそ注意するようにした点と、ネットワークを GAN の要領で敵対的に学習した点でしょうか。遠い未来の予測値はそこに至るまでの予測値の系列を再帰的に利用して生成するわけですから、あたかも本物と見紛うような予測値の系列を生み出す必要があるわけで、GAN を用いて学習するというのはイメージとして合っているような気がします。

他方、こちらの「Informer」はやはり Transformer が遠い過去の情報を掴めることを利用しているわけですが、Transformer を時系列に応用するにあたって以下が問題だといっていますね。

セルフアテンションする以上、系列長 $L$ に対して $\mathcal{O}(L^2)$ の計算量がかかる。
セルフアテンション層を積み重ねる原理上、推論時に膨大なメモリを要する。
推論に時間がかかる（再帰的に推論するため）。

1. や 2. は確かに Transformer の一般的な難点と思います。3. は1つの文章を分類などする分には気にならない点と思いますが。「AST」では 1. や 2. のような計算量やメモリについて何か言及していましたっけ？

していなかった気がするけどな…でも、Transformer を時系列に応用するにあたってその系列長に関する計算量のボトルネックを何とかしようという話ならむしろ NeurIPS2019 にあったよね。以下の記事の中の「Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting」かな。このモデルの通称は「LogSparse Transformer」だね。

雑記： NeurIPS 2019 Proceedings の「時系列」を含むタイトル

趣旨が同じだから当然「Informer」からも「LogSparse Transformer」は引用されているね。というか6ページ目の検証結果の Table 1 や Table 2 内で「LogTrans」とされて比較手法になっているね（今回の提案手法でのセルフアテンションの仕方の有効性を確かめるためにセルフアテンションの仕方だけを置き換えた形だと思うけど）。表をみると「LogTrans」は Table 2 の多変量時系列予測部門の ECL データセットの1週間後、2週間後予測で優勝しているね。他の予測でも提案手法に肉薄している気もするけど。

うおお勝手に先を読まないでください。アブストラクトに戻ると今回の「Informer」は上記の問題に対し、

「ProbSparse」なるアテンション手法で特徴抽出性能を維持しつつ計算量を $\mathcal{O}(L \log L)$ に抑えた。
「セルフアテンション蒸留」で系列長を削減していくことでメモリ使用量を抑えた。
「生成的デコーダ」によって1ステップでの長期予測を達成し推論速度を大幅に向上させると共に、誤差の蓄積も抑えた。

のように対処したとのことですが…ともかく本文に入ると、既存の時系列予測モデルは基本的に長期予測に耐えるようにできていないということですね。Figure 1 (c) のように「LSTM で長期予測をしたら遠い未来を予測するほど誤差は増えていき、その1点の予測値を得る時間も増える」と。なお、この Figure 1 (c) の LSTM は何を学習したものかというと、ETT データセット（著者が作成したデータセット；後述）の1時間ごとの変電所の変圧器の油温を、直近の12点（つまり半日分）を用いて未来を予測するように学習したもので、Figure 1 (c) では最長で480点先（20日後）まで予測したということですね。20日後の変圧器の油温の予測とは果てしない気がしますが…。

でもよく知らないけど電気を発電するなら20日くらい前から石油なり石炭なりを発注しておく必要とかあったりするんじゃないのかな。と考えると遠い未来に送電すべき量がわかるに越したことはない気はするけど、その推論速度がそんなにシビアなのかとか、信頼区間を予測した方がいいのではとかは思うかな。「生成的デコーダ」を導入した効果は推論速度よりも「誤差の蓄積を抑えた」という方が重要そうに思うんだよね。「誤差の蓄積を抑えた」というよりは、「長期予測を想定していない従来手法を無理にそのまま再帰的に利用すると誤差が蓄積されるので、長期予測にフォーカスするなら異なる枠組みを導入した方がよい」という感じがするけど。

私にいわれましても…まあそれで、遠い過去の情報を活用するとなると、過去の入力を再帰を介さずに直接「注意」しにいける Transformer に白羽の矢が立つわけですが、先に述べた通りの難点があるわけです。「セルフアテンションの威力がこそボトルネックになってしまう」と…いや何のデメリットもなくおいしい話はそうないと思いますが…。ともかくそのボトルネックを何とかしようとしにいくわけですが、何もボトルネックを何とかしようという研究はこれまでもあったわけです。列挙されているものは以下ですね。

Compressive Transformer（Rae et al. 2019）
Sparse Transformer（Child et al. 2019）	Transformer を画像にも適用しているんですね。これは論文の3ページ目の Figure 3. をみるに、アテンションの行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ を完全に計算することを捨てた、といった感じがします。あるステップからどのステップに注目するかを相対位置または絶対位置に制限してしまうといったような。これは実際データに対して「この箇所に文脈として効くのはこの範囲だろう」という事前知識があれば有効でしょう。しかし、事前知識がないときには利用しづらそうに思います。
LogSparse Transformer（Li et al. 2019）	これは件の NeurIPS2019 の論文ですね。5ページ目の図をみるに、これもアテンションの行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ を完全に計算することを捨てていますが、相対位置や絶対位置でフィルタするのではなく、「近くは綿密に、遠くにいくほど大雑把に」といった感じでもう少し情報の拾い漏れを防いでいるのでしょうか。
Reformer（Kitaev et al. 2019）	これも計算量を $\mathcal{O}(L \log L)$ にしていますがより技巧的にみえます。論文の4ページ目に絵があります。なんというか、処理するステップたちをあるルールで「青組、黄組、赤組、白組」に組分けした上で人口の多い組から順に並べ、等間隔にサブ系列に切って、「サブ系列内 or 自分の組内のみでアテンションする」といった感じです。それで組分けのルール locality sensitive hashing が肝心ですが、これは3ページ目の図でしょうか。点 x とその少し後ろにいる点 y があったとして、点 x をランダムに回転させたときに同じ色のエリアにいるか、といった絵にみえますが…後で実装をみてみましょう。
Linformer（Wang et al. 2020）	セルフアテンション内での射影の行列を低ランク近似することで $\mathcal{O}(L)$ を達成しているのですかね。しかし時系列の長期予測の場合は行列が固定できない故に $\mathcal{O}(L^2)$ まで劣化する可能性があるとありますが…？
Transformer-XL（Dai et al. 2019）	これらは「補助隠れ状態」を用いることで計算量を抑えつつ遠い過去の情報を利用できるようにしたようですが、であれば今回用いられたアプローチとは違いますね。これらのアプローチは時系列には応用できるのでしょうか…？

何にせよこれらでは「時系列の長期予測」という目的を達成するのに不十分といっているわけです。問題点の 1. の計算量にしか対処していないと。そもそも「LogSparse Transformer」を除いて時系列の予測を企図していませんし、「LogSparse Transformer」も長期予測を主眼においてはいないと思いますが。

問題点の 3. は長期予測に独特だからともかく、2. の必要メモリへの取り組みはあったんじゃないのかな。そのまま「蒸留BERT」なるモデルが公開されていて Linformer でも引用されているし、さらに「貧乏人のためのBERT」なんていう論文もあるよ。今回の手法とは枠組みが違うのかな？

BERT を動かせない人が貧乏なのではありません、BERT を動かせる計算資源を利用できる人がお金持ちなのです…。

モデル

気を取り直してモデルの詳細に入りましょう。まずモデルの入出力は、

モデルの入力は $d_x$ 次元ベクトルが $L_x$ 個並んだもの $\mathcal{X}^t = \{x_1^t, \cdots, x_{L_x}^t\}$ です。
モデルが出力すべきは $d_y$ 次元ベクトルが $L_y$ 個並んだもの $\mathcal{Y}^t = \{y_1^t, \cdots, y_{L_y}^t\}$ です。つまり、長期予測といっても、遠い未来の1点ではなく、遠い未来までのすべての点の予測を目指すということを含意していると思います。

そしてまず Self-Attention の話がありますね。Self-Attention の復習として下に絵を描いてみました。これは "I understand." という文章（ピリオドも1トークンとしさらに先頭トークンと末尾トークンを追加すれば5トークンからなる）を流したときのイメージで、アテンションの行列の数値は実際にこの文章を bert-large-cased 学習済みモデルに流して書き出したものです。であれば実際はヘッド数は16あるんですが面倒なので4ヘッドしか描いていません。bert-large-cased では入力特徴及び出力特徴の次元数は1024次元で、1ヘッドあたりが出力するのは64次元ですね。図中の $d=64$ ということです。

うん、自然言語処理では普通「文章長さ＜特徴次元数」だからその図の入出力みたいに横長の長方形になるわけだよね。でも今回は長期予測をしたいから、Table 1, Table 2 にある数値の単位がステップ数で合っているなら予測部分だけで960ステップ流したいことになるよね。BERTには256ステップ以上流せない設定になっているくらいだから、長いわけだね。計算量は流すステップの長さを $L$ とするなら $QK^\top$ の部分の行列積が $\mathcal{O}(L \cdot d \cdot L)$ で、最後のアテンションを適用するときの行列積が $\mathcal{O}(L \cdot L \cdot d)$ だから、 $d$ を定数扱いすれば $\mathcal{O}(L^2)$ だね。

ええまさにそのような話が続きます。なので計算量が $\mathcal{O}(L^2)$ になることを割けるべく、これまで Sparse Transformer や LogSparse Transformer は行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ （面倒なのでこれ以降セルフアテンション行列とよびます）の成分を全て計算するのではなく間引きをやってきたわけですが、幾分ヒューリスティックな回避策であったわけです。それに、全ての Multi-Head で同じ間引き方をしていたと…そうなんですか？いやいわれてみれば Head ごとに間引き方を変えるべきですよね…。ともかく、現実にはセルフアテンション行列は疎であるということです。まあ特に自然言語処理では過去の単語たちをべったり注意することもないでしょうね。しかしどのように疎なのかがわからないから間引き方がわからないのですが…読み進めると3ページ目の2段目の最上部では、あるステップから各ステップをどれだけ注意するかの分布 $p$ と、一様分布 $q$ のKLダイバージェンスを取っていますね。なるほど一様分布から逸脱しているほど特定のステップに着目し、重要な情報を掴んでいる見込みが高いというわけでしょうか。以下の図でも計算してみました。

f:id:cookie-box:20210211142747p:plain:w520

上図の一番最後の式の第1項は定数なので無視して、第2項と第3項が式 (2) の $M(q_i, K)$ に相当しますね。論文中では sparsity measurement とよばれていますが、「ステップ $i$ からの各ステップへの注意分布の一様分布からの逸脱度」です（以下この記事中では逸脱度とよびましょう）。そしてセルフアテンション行列の各行のうち、逸脱度が高い $u$ 本のみを残すと。 $u$ を $\log L$ に比例させるようにとれば計算量は $\mathcal{O}(L \log L)$ になると…いやいやいや！そもそもセルフアテンション行列を得る計算量が $\mathcal{O}(L^2)$ なわけですよね？セルフアテンション行列が得られた上で「この $u$ 本だけ残そう」では意味がないですよね？？

続きを読もう。しかし逸脱度自体を得るのに $\mathcal{O}(L^2)$ かかってしまう、だから逸脱度を近似するというようにあるよ。まず補題1で逸脱度の上下限を示しているね。上下限がこうなるのは上図の式と見比べればわかる。それでこの上限の方を、完全なセルフアテンション行列からではなく、サンプリングした一部の要素だけ計算したセルフアテンション行列から見積もる。 $Q, K$ の分布の形にある程度の仮定をおけば、 $Q$ の行と $K^\top$ の列の組を $L \log L$ 組サンプリングすることで見積もれるって。そのことをきちんと示したのが命題1かな。 $k_j$ が正規分布にしたがうとしているのはどれくらい適切なのかわからないけど。まあ確かに分布が一様分布から離れているかって、分布の一番高いところが高かったらそれは離れているし、各行の最大値を見積もるだけなら行列の要素を全て計算しなくてもよさそうだよね。

サンプリングの仕方は追えていませんが、一様分布から離れているかどうかというのは、過去のヒューリスティックな回避策に比べれば積極的に意味のあるアテンションを残そうとしていますね。

セルフアテンションの計算量の問題が片付いたら次はメモリの問題でしたっけ。モデルサイズの問題といってもいいのでしょうか。セルフアテンション時の計算量を間引いても、セルフアテンション層をどんどん積み重ねるならパラメータ数とメモリ使用量は増えるばかりです。

その問題については論文4ページ目の Figure 3 をみるに、セルフアテンション層を抜ける度に Conv1D + MaxPool1D することで系列の長さを半分にしているようにみえるね。あ、この図では Attention Block という薄オレンジの直方体の中にガラス板（？）が4枚浮かんでいるようにみえるけど、これは4つのヘッドのセルフアテンション行列だね。式 (5) をみると Conv1D を適用した後に ELU で活性化している。

ELU — PyTorch 1.7.1 documentation

では最後はここまで改造した Transformer を用いてどのように推論するのかという問題ですか。1ステップずつ再帰的に読み出していくのでは時間がかかるというより誤差が積み重なっていくのですよね？

それについてはそのまま「1ステップで読み出すようにした」という感じにみえるな。以下にイメージ図を描いたよ。水色が目的変数でピンク色が説明変数（タイムスタンプなど）ね。本文中の例では、向こう7日分を予測するのに、デコーダにここまでの5日分をフィードするみたい。それで予測してほしい箇所はゼロにした状態（いわば「プレースホルダ」）を渡してそこに埋まるものを返してねって感じなんだけど、エンコーダに渡す期間とデコーダに渡す期間が把握できていないから、以下の図は GitHub の Informer の実装をみて描き直すかもしれないかな…。それで損失関数は MSE とあるね。検証したのは全部回帰タスクみたいだし。特に言及がないから、近い未来の誤差も遠い未来の誤差も重さは等しいということなのかな？

f:id:cookie-box:20210214014501p:plain:w290

検証データと比較手法

ではモデルについては一通り確認したので検証されたデータセットをみてみましょう。「電気」「電気」「天気」といったところでしょうか。

ETT (Electricity Transformer Temperature)	これは著者らが収集されたデータなのですね。以下に公開されているようです。 GitHub - zhouhaoyi/ETDataset: The Electricity Transformer dataset is collected to support the further investigation on the long sequence forecasting problem. Electricity Transformer Temperature という言葉が聞き慣れないですが、このデータセットは「変圧器の油温」を予測することを企図したものであるようです。よくわからないのですが、変圧器の油温というのが上昇しすぎると危険であって、変圧器に負荷がかからないように送電するために重要な指標ということなんでしょうか。説明変数には High UseFul Load などが含まれていますがこれは最大実効負荷などと訳すのでしょうか。ともかく、ETT-small-m1, ETT-small-m2 というのが中国のある2つの省の分単位のデータであって2年×365日×24時間×60分=1,051,200点のデータを含むそうです。時間単位になっている ETT-small-h1, ETT-small-h2 なるデータもあるようですね。
ECL (Electricity Consuming Load)	また電気ですが、お馴染みの UCI Machine Learning Repository のデータですね。 UCI Machine Learning Repository: ElectricityLoadDiagrams20112014 Data Set このデータは NeurIPS2018 の Deep State Space Models for Time Series Forecasting や NeurIPS2020 の AST でも利用されていました。ある期間におけるポルトガルの370人の個々の顧客の15分ごとの電力消費量です。
Weather	アメリカの1600地点での1時間毎の気候データでしょうか。論文中のリンクは以下に転記してみましたが、この記事をかいている時点で重すぎてアクセスできる気配がないのですよね…。 https://www.ncdc.noaa.gov/orders/qclcd/

そして比較対象となっている手法は以下です。

ARIMA	ARIMA は ARIMA ですね。ただ ARIMA の参考文献として以下が引用されているのは何故なんでしょうか。 (PDF) Stock price prediction using the ARIMA model
Prophet	Prophet も Prophet です。
LSTMa	LSTMa とは…？これは機械翻訳の論文のようですが、LSTM を普通に利用するのではなく、LSTM の各ステップの特徴を用いてデコードするコンフィギュレーションのことを LSTMa というのでしょうか。間違っていたらごめんなさい。
LSTnet	LSTnet は以下の論文を読んだときに引用されていましたね。絵も描きました。畳込みと再帰のハイブリッドモデルさんでしたね。論文読みメモ： Think Globally, Act Locally: A Deep Neural Network Approach to High-Dimensional Time Series Forecasting（その1） - クッキーの日記
DeepAR	DeepAR も DeepAR です。AST でも DeepAR の敵対的学習を試行されていましたね。ただ DeepAR は後続に Deep State Space Models があったと思いますがそちらは利用できないものなのでしょうか。

さらに、これらのモデルとは別に、「ProbSparse」によるセルフアテンションの有効性の検証として、今回のモデルのセルフアテンション部分のみを「通常のセルフアテンション」「Reformer のセルフアテンション」「LogSparse Transformer のセルフアテンション」に置き換えたモデルも比較対象にエントリーされています。公平を期すために、どのモデルのコンフィギュレーションも1GPUで推論可能なように調整されているようです（通常のセルフアテンションもなんでしょうか？）。

その結果が Table 1, Table2 ですね。ほとんどのタスクで Informer が最高精度を達成しています…って、通常のセルフアテンションよりも高精度が出ているタスクが多いのですね。Informer はセルフアテンション行列の計算を間引いたのに間引かないよりも性能がよいとはなぜなのでしょう？

取るに足らないアテンションなら最初から要らなかったということだよね。単変量予測の Table 1 で目立つのは ECL データの 48, 168, 336 ステップ先予測で DeepAR が健闘しているね。どうしてなんだろう？

私にいわれましても…。多変量予測の Table 2 もだいたい Informer 眷属の独断場ですがたまに LSTnet さんが健闘していますね。

Table 2 のモデルの中でさ、畳込みも再帰も利用しているのって LSTnet だけだよね。Transformer は特殊な畳込み扱いとして。逆に色々使っている LSTnet が少ししか勝てないのが Transformer の威力なんじゃないのかな。

私にいわれましても…。セルフアテンション手法の Reformer は精度が奮わないですね。時系列データと相性が悪いんでしょうか。Table 4 はセルフアテンション蒸留をしない場合の参考記録ですね。ハイフンになっている箇所はアウトオブメモリーと。フィードする入力系列の長さが同じならさすがに蒸留しない方が高精度は出ますが、如何せん入力系列の長さが食えないので結局蒸留した方がよい、といえそうです。Table 5 は再帰的にデコードした場合の結果で…再帰的なデコードでは誤差が大きすぎてもうお話にならなかったようですね。

一旦おわり

2021-01-31

雑記：分散共分散行列のベイズ更新の話

雑記

2021-02-02 絵を追加しました。

いろいろな場面（カルマンフィルタ、ガウス過程回帰など、直接観測できない何かの分布をその線形変換の観測からベイズ更新する場面）で以下の問が出てくると思います。

$x \in \mathbb{R}^n$ は確率ベクトルでその事前分布は平均 $0$ で分散共分散行列が $V \in \mathbb{R}^{n \times n}$ の多変量正規分布です。
$y \in \mathbb{R}^m$ も確率ベクトルで $y = Hx + w$ です。 $H \in \mathbb{R}^{m \times n}$ は行列です。 $w \in \mathbb{R}^m$ は平均 $0$ で分散共分散行列が $R \in \mathbb{R}^{m \times m}$ の多変量正規分布にしたがうノイズで $x$ とは独立です。
いまある $y$ が観測されました。この $y$ の下での（＝事後分布の） $x$ の分散共分散行列はどうなりますか？

普通はベイズの定理で $x$ の確率密度関数を考えると思います。

方法1．ベイズの定理で $x$ の確率密度関数をかく

$\begin{split} \displaystyle p(x|y) \propto p(y|x)p(x) &\propto \exp \left( -\frac{1}{2} (Hx)^\top R^{-1} Hx\right) \exp \left( -\frac{1}{2} x^\top V^{-1} x\right) \\ &= \exp \left( -\frac{1}{2} x^\top (V^{-1} + H^\top R^{-1} H) x\right) \end{split}$

より $x$ の事後分散共分散行列は $(V^{-1} + H^\top R^{-1} H)^{-1}$ である。

こうすると観測前は精度行列（分散共分散行列の逆行列で、多変量正規分布の密度関数の式で確率ベクトルに挟まれているやつ）が $V^{-1}$ だったのが観測後は $V^{-1} + H^\top R^{-1} H$ になっていて、精度が大きくなった（＝分散が小さくなった）感があります。観測の精度 $R^{-1}$ が大きいならより精度はより大きくなるし、 $H=0$ なら（観測が $x$ を反映しないなら）精度は全く大きくならないこともわかります。

別に以上でいいんですが、上の方法は終始 $x$ の精度の世界で考えていて、 $x$ の分散に何があったのかわかりにくいものになっています（？）。そもそも $y$ が観測されたら $x$ の分布がどうなるのかというのは $(x,y)$ の同時分布を考えるのが正攻法であるはずです（？）。なのでそれでやってみます。また、ここでは（※）の箇所で後述の補題を利用します（条件付き共分散をとる方法は色々あると思いますが、この補題は直接的に条件付き共分散はこれですというものなので利用しました。これは行列をブロック単位で UDL 分解するのと等価です）。

方法2． $(x,y)$ の同時分布を出してから $x$ の分散共分散行列を取り出す
多変量正規分布のモーメント母関数は $M_X(t) = E(e^{t^\top X}) = \exp \Bigl( \mu^\top t + \frac{1}{2} t^\top \Sigma t \Bigr)$ なので、 $(x,y)$ の同時分布のモーメント母関数は以下のようになる。

$\displaystyle \begin{split} E \left[ e^{ \left( \begin{array}{cc} t_1^{\top} & t_2^{\top} \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)} \right] &= E \left[ e^{ t_1^{\top} x + t_2^\top H x + t_2^\top w} \right]= E \left[ e^{ t_1^{\top} x + t_2^\top H x} \right] E \left[ e^{ t_2^\top w} \right] \\ &= \exp \Bigl( \frac{1}{2} t_2^\top R t_2 \Bigr) \exp \Bigl( \frac{1}{2} (t_1^\top + t_2^\top H) V (t_1 + H^\top t_2) \Bigr) \\ &= \exp \Bigl( \frac{1}{2} \left( t_1^\top V t_1 + t_1^\top V H^\top t_2 + t_2^\top H V t_1 + t_2^\top HVH^\top t_2 + t_2^\top R t_2 \right) \Bigr) \\ &= \exp \left( \frac{1}{2} \left( \begin{array}{cc} t_1^{\top} & t_2^{\top} \end{array} \right) \left( \begin{array}{cc} V & VH^\top \\ HV & HVH^\top + R \end{array} \right) \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right) \right) \end{split}$

よって $(x,y)$ の同時分布は分散共分散行列が $\displaystyle \tilde{V}_{x,y} = \left( \begin{array}{cc} V & VH^\top \\ HV & HVH^\top + R \end{array} \right)$ の多変量正規分布である。このとき $x$ の分散共分散行列 $\tilde{V}_{x}$ は $\tilde{V}_{x,y}$ の右下 $m \times m$ ブロックに対するシューア補行列（※）に他ならず、したがって $V - VH^\top (HVH^\top + R)^{-1} HV$ である。

こうすると観測前は分散が $V$ だったのが観測後は $V - VH^\top (HVH^\top + R)^{-1} HV$ になっていて分散が小さくなった感があります。（※）では以下の補題を利用しました（参考： Sherman-Morrison-Woodburyの公式 (Schur補行列) - いんふらけいようじょのえにっき）。

補題（シューア補行列）
正方行列 $P \in \mathbb{R}^{(n+m) \times (n+m)}$ を $A \in \mathbb{R}^{n \times n}, \, D \in \mathbb{R}^{m \times m}$ が正方行列になるように $\displaystyle P = \left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$ と区分けする。このとき $P$ も $D$ も正則ならば、 $S = A - BD^{-1}C$ も正則で $P^{-1}$ の左上 $n \times n$ ブロックは $S^{-1}$ になる。この $S$ を $P$ の $D$ に関するシューア補行列とよぶ。

証明は元の記事にありますが、記事中で示されているのは左上ブロックに対するシューア補行列の方なので、LDU 分解を UDL 分解に変更して右下ブロックに対するシューア補行列の方を示してください。同時共分散行列の LDU 分解には $y$ の共分散が陽にあらわれ、UDL 分解には $x$ の共分散が陽にあらわれます（以下）。なので $x$ の共分散がほしいときは UDL 分解するのが自然なはずです。上の補題は UDL 分解の $\tilde{X}$ が $A - BD^{-1}C$ であるといっているのと同じです。

LDU 分解すると以下の $Y$ が $y$ の共分散： $\displaystyle \left( \begin{array}{cc} t_1^\top & t_2^\top \end{array} \right) \left( \begin{array}{cc} I & O \\ W & I \end{array} \right) \left( \begin{array}{cc} X & O \\ O & Y \end{array} \right) \left( \begin{array}{cc} I & Z \\ O & I \end{array} \right) \left( \begin{array}{c} t_1^\top \\ t_2^\top \end{array} \right) = \left( \begin{array}{cc} t_1^\top + t_2^\top W & t_2^\top \end{array} \right) \left( \begin{array}{cc} X & O \\ O & Y \end{array} \right) \left( \begin{array}{c} t_1 + Z t_2 \\ t_2 \end{array} \right)$
UDL 分解すると以下の $\tilde{X}$ が $x$ の共分散： $\displaystyle \left( \begin{array}{cc} t_1^\top & t_2^\top \end{array} \right) \left( \begin{array}{cc} I & \tilde{Z} \\ O & I \end{array} \right) \left( \begin{array}{cc} \tilde{X} & O \\ O & \tilde{Y} \end{array} \right) \left( \begin{array}{cc} I & O \\ \tilde{W} & I \end{array} \right) \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right)= \left( \begin{array}{cc} t_1^\top & t_1^\top \tilde{Z} + t_2^\top \end{array} \right) \left( \begin{array}{cc} \tilde{X} & O \\ O & \tilde{Y} \end{array} \right) \left( \begin{array}{c} t_1 \\ \tilde{W}t_1 + t_2 \end{array} \right)$

なお、方法1．の結論は $(V^{-1} + H^\top R^{-1} H)^{-1}$ で、方法2．の結論は $V - VH^\top (HVH^\top + R)^{-1} HV$ で、なんか違ってみえますが、以下の Sherman-Morrison-Woodbury の公式よりこれらは等しいです。というかむしろ方法1．と方法2．で事後分散共分散行列を求めると Sherman-Morrison-Woodbury の公式が証明できることになります（まともな証明は先の記事にありますが、LDU 分解と UDL 分解の逆行列の成分比較によります）。

Sherman-Morrison-Woodbury の公式

$A \in \mathbb{R}^{n \times n}, \, B \in \mathbb{R}^{n \times m}, \, C \in \mathbb{R}^{m \times n}, \, D \in \mathbb{R}^{m \times m}$ について、 $A$ も $D - CA^{-1}B$ も $D$ も $A - BD^{-1}C$ も正則なとき、以下の恒等式が成り立つ。

$(A - BD^{-1}C)^{-1} = A^{-1} + A^{-1} B (D - CA^{-1}B)^{-1} C A^{-1}$

では $(V^{-1} + H^\top R^{-1} H)^{-1}$ と $V - VH^\top (HVH^\top + R)^{-1} HV$ のどちらの表現が便利なのかというと、逆行列が取られている行列が前者は $n \times n$ 、後者は $m \times m$ なので、 $m$ が大きければ前者、 $n$ が大きければ後者が逆行列の計算コストが低いはずです（なので推定対象の状態空間が高次元の場合は方法1．で前者を求めてから Woodbury の公式で後者にしましょうとかいわれると思います）。

それで、どうして方法1．と方法2．で逆行列をとる行列のサイズに違いが出てくるのか気になるわけですが、トートロジカルですがどこの行列が正則であることを利用しているかが違うはずです。

方法1．：ベイズの定理を使う場合だと、終始「密度の積（精度の和）」で考えるので逆行列を取るのは最後の仕上げになり、 $x$ の精度行列＝ $n \times n$ 行列の逆行列をとることになります。
方法2．：同時分布の分散共分散行列を出してから補題（シューア補行列）を利用する場合だと、この操作で直接利用するのは同時共分散行列の右下ブロックが正則であることです。
- シューア補行列 $S$ が存在するならば $S = A - BD^{-1}C$ であることを示すときに利用するのは $D$ が正則であることだけです。
- なお、同時共分散行列の LDU 分解の $P^{-1}$ と成分比較することもできます。この場合は左上 $n \times n$ ブロックの $A$ が正則であることを利用することになり、また、出てくる答えが方法1．と同じになります（方法2．の $\tilde{V}_{x,y}$ の各ブロックを $A^{-1}+A^{-1}B(D - CA^{-1}B)^{-1} CA^{-1}$ に代入）。なので、同時共分散行列を経由することではなく、そこから如何に $x$ の共分散行列をとるかが逆行列のサイズを決めています。

方法1．

「 $x$ の事前共分散行列」
　↓　ベイズの定理
「 $x$ の事後精度行列」
　↓　逆行列 ― 精度行列全体 $n \times n$ が正則であることを利用
「 $x$ の事後共分散行列」

方法2．

「 $x$ の事前共分散行列」
　↓　 $(x,y)$ の同時分布のモーメント母関数
「 $(x,y)$ の同時共分散行列」
　↓　補題（シューア補行列）― 同時共分散行列の右下 $m \times m$ ブロックが正則であることを利用
「 $x$ の事後共分散行列」

まとめると（まとめではない）、 $(x, y)$ の同時共分散行列を $P$ とおくとベイズの定理は精度行列 $P^{-1}$ の UDL 分解（ $P$ の LDU 分解）の左上ブロックをとることに他ならず、それに Woodbury の公式を適用すると $P^{-1}$ の LDU 分解（ $P$ の UDL 分解）の左上ブロックになるので正則を仮定するブロックが左上から右下に切り替わる、という感じがします（無論ベイズ更新の文脈ではどちらも正則でないと困るのですが正則であることを明示的に利用するのがどちらなのかが切り替わる）。

2021-02-02 追記

絵を描きました。スタートから出発してゴールを目指します。★は逆行列の操作なので大きな逆行列はなるべく避けます。ただし図は $n > m$ のイメージで描いています。この大小関係によって適切なルートを選びます。

f:id:cookie-box:20210202184504p:plain