2021-02-11

論文読みメモ： Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

論文読み

2021-02-14 3枚目の絵を修正しました。

以下の論文を読みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

Haoyi Zhou, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, Wancai Zhang. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. arXiv preprint arXiv:2012.07436, 2020.
[2012.07436] Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
GitHub - zhouhaoyi/Informer2020: The GitHub repository for the paper "Informer" accepted by AAAI 2021.

まとめ

遠い過去のステップも直接「注意」しにいける Transformer は時系列データの長期予測に有用と考えられるが、長い系列を Transformer に流すには以下の難点がある。

セルフアテンションする以上、系列長 $L$ に対して $\mathcal{O}(L^2)$ の計算量がかかる。
セルフアテンション層を積み重ねる原理上、推論時に膨大なメモリを要する。
推論に時間がかかる（再帰的にデコードするため）（誤差の蓄積の問題もある）。

そこで提案モデル「Informer」ではこれらの難点を以下のように克服した。

「ProbSparse」というセルフアテンション手法で特徴抽出性能を維持しつつ計算量を $\mathcal{O}(L \log L)$ に抑えた。

方針として、 ${\rm Softmax}(QK^\top /\sqrt{d}) \in \mathbb{R}^{L \times L}$ の各行のうち一様分布からの逸脱度が大きい行（＝重要な「注意」を含んでいる見込みが高い）だけを残し他の行は捨てる。サンプリングによって逸脱度を見積もる。

セルフアテンション層を出る度に Conv1D + MaxPool1D して系列の長さを半分にしていくことでメモリ使用量を抑えた（セルフアテンション蒸留）。
再帰的にデコードするのではなく一気にデコードすることで推論速度を大幅に向上させた（生成的デコーダ）。

この「Informer」はデータセット「Electricity Transformer Temperature（著者による変電所の変圧器の油温データ）」、「Electricity Consuming Load」、「Weather」を使用したさまざまな長期予測タスク（単/多変量予測 × 24～960ステップ先予測）のほとんどで既存手法（ARIMA、Prophet、LSTMa、LSTnet、DeepAR）を上回る精度を示した。また、

「ProbSparse」によるセルフアテンションの有効性の検証として、「通常のセルフアテンション」「Reformer のセルフアテンション」「LogSparse Transformer のセルフアテンション」に置き換えたモデルとも比較されたが、やはりほとんどのタスクでこれらのモデルよりも高い精度を示した。特に、通常のセルフアテンション（計算量大）よりもむしろ精度がよいケースが多かった（＝「ProbSparse」による取捨選択が功を奏した）。
セルフアテンション蒸留の有効性の検証として、セルフアテンション蒸留しないモデル構造とも比較されたが、入力系列の長さが同じであれば蒸留しないモデルの方が精度が出るが、蒸留しないモデルでは入力系列を長くするとアウトオブメモリーになるので、結局セルフアテンション蒸留をした方がよかった。
生成的デコーダの検証として再帰的にデコードするモデルとも比較されたが、再帰的にデコードするモデルでは誤差が大きすぎた。

所感

提案した3コンポーネント全ての有効性を示している。
セルフアテンションの計算量の削減の仕方が、先行研究の LogSparse Transformer のように「近くは綿密に計算するが遠くにいくほどどんどんとばす」という幾分アドホックなものではなく、積極的に何かを強く注意している行を優先して残そうとするものになっている。その有効性は通常のセルフアテンションの予測性能を上回っていることで示されている。
NeurIPS2020 の Adversarial Sparse Transformer は Transformer を敵対的に学習することで長期予測における誤差の蓄積を回避したが、そもそも再帰的に予測したいという要請がなければ Informer のように一度に予測すればよいと考えられる。

導入
モデル
検証データと比較手法

導入

f:id:cookie-box:20190101155733p:plain:w60

この「Informer」は「Transformer による時系列の長期予測」とのことですが、つい最近も「Transformer による時系列の長期予測」をみた気が…以下の「AST（Adversarial Sparse Transformer）」ですね。

NeurIPS2020読みメモ： Adversarial Sparse Transformer for Time Series Forecasting

「AST」が工夫した点は α-entmax を用いてアテンションを疎にし重要な情報をこそ注意するようにした点と、ネットワークを GAN の要領で敵対的に学習した点でしょうか。遠い未来の予測値はそこに至るまでの予測値の系列を再帰的に利用して生成するわけですから、あたかも本物と見紛うような予測値の系列を生み出す必要があるわけで、GAN を用いて学習するというのはイメージとして合っているような気がします。

他方、こちらの「Informer」はやはり Transformer が遠い過去の情報を掴めることを利用しているわけですが、Transformer を時系列に応用するにあたって以下が問題だといっていますね。

セルフアテンションする以上、系列長 $L$ に対して $\mathcal{O}(L^2)$ の計算量がかかる。
セルフアテンション層を積み重ねる原理上、推論時に膨大なメモリを要する。
推論に時間がかかる（再帰的に推論するため）。

1. や 2. は確かに Transformer の一般的な難点と思います。3. は1つの文章を分類などする分には気にならない点と思いますが。「AST」では 1. や 2. のような計算量やメモリについて何か言及していましたっけ？

f:id:cookie-box:20190101160814p:plain:w60

していなかった気がするけどな…でも、Transformer を時系列に応用するにあたってその系列長に関する計算量のボトルネックを何とかしようという話ならむしろ NeurIPS2019 にあったよね。以下の記事の中の「Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting」かな。このモデルの通称は「LogSparse Transformer」だね。

雑記： NeurIPS 2019 Proceedings の「時系列」を含むタイトル

趣旨が同じだから当然「Informer」からも「LogSparse Transformer」は引用されているね。というか6ページ目の検証結果の Table 1 や Table 2 内で「LogTrans」とされて比較手法になっているね（今回の提案手法でのセルフアテンションの仕方の有効性を確かめるためにセルフアテンションの仕方だけを置き換えた形だと思うけど）。表をみると「LogTrans」は Table 2 の多変量時系列予測部門の ECL データセットの1週間後、2週間後予測で優勝しているね。他の予測でも提案手法に肉薄している気もするけど。

うおお勝手に先を読まないでください。アブストラクトに戻ると今回の「Informer」は上記の問題に対し、

「ProbSparse」なるアテンション手法で特徴抽出性能を維持しつつ計算量を $\mathcal{O}(L \log L)$ に抑えた。
「セルフアテンション蒸留」で系列長を削減していくことでメモリ使用量を抑えた。
「生成的デコーダ」によって1ステップでの長期予測を達成し推論速度を大幅に向上させると共に、誤差の蓄積も抑えた。

のように対処したとのことですが…ともかく本文に入ると、既存の時系列予測モデルは基本的に長期予測に耐えるようにできていないということですね。Figure 1 (c) のように「LSTM で長期予測をしたら遠い未来を予測するほど誤差は増えていき、その1点の予測値を得る時間も増える」と。なお、この Figure 1 (c) の LSTM は何を学習したものかというと、ETT データセット（著者が作成したデータセット；後述）の1時間ごとの変電所の変圧器の油温を、直近の12点（つまり半日分）を用いて未来を予測するように学習したもので、Figure 1 (c) では最長で480点先（20日後）まで予測したということですね。20日後の変圧器の油温の予測とは果てしない気がしますが…。

でもよく知らないけど電気を発電するなら20日くらい前から石油なり石炭なりを発注しておく必要とかあったりするんじゃないのかな。と考えると遠い未来に送電すべき量がわかるに越したことはない気はするけど、その推論速度がそんなにシビアなのかとか、信頼区間を予測した方がいいのではとかは思うかな。「生成的デコーダ」を導入した効果は推論速度よりも「誤差の蓄積を抑えた」という方が重要そうに思うんだよね。「誤差の蓄積を抑えた」というよりは、「長期予測を想定していない従来手法を無理にそのまま再帰的に利用すると誤差が蓄積されるので、長期予測にフォーカスするなら異なる枠組みを導入した方がよい」という感じがするけど。

私にいわれましても…まあそれで、遠い過去の情報を活用するとなると、過去の入力を再帰を介さずに直接「注意」しにいける Transformer に白羽の矢が立つわけですが、先に述べた通りの難点があるわけです。「セルフアテンションの威力がこそボトルネックになってしまう」と…いや何のデメリットもなくおいしい話はそうないと思いますが…。ともかくそのボトルネックを何とかしようとしにいくわけですが、何もボトルネックを何とかしようという研究はこれまでもあったわけです。列挙されているものは以下ですね。

Compressive Transformer（Rae et al. 2019）
Sparse Transformer（Child et al. 2019）	Transformer を画像にも適用しているんですね。これは論文の3ページ目の Figure 3. をみるに、アテンションの行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ を完全に計算することを捨てた、といった感じがします。あるステップからどのステップに注目するかを相対位置または絶対位置に制限してしまうといったような。これは実際データに対して「この箇所に文脈として効くのはこの範囲だろう」という事前知識があれば有効でしょう。しかし、事前知識がないときには利用しづらそうに思います。
LogSparse Transformer（Li et al. 2019）	これは件の NeurIPS2019 の論文ですね。5ページ目の図をみるに、これもアテンションの行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ を完全に計算することを捨てていますが、相対位置や絶対位置でフィルタするのではなく、「近くは綿密に、遠くにいくほど大雑把に」といった感じでもう少し情報の拾い漏れを防いでいるのでしょうか。
Reformer（Kitaev et al. 2019）	これも計算量を $\mathcal{O}(L \log L)$ にしていますがより技巧的にみえます。論文の4ページ目に絵があります。なんというか、処理するステップたちをあるルールで「青組、黄組、赤組、白組」に組分けした上で人口の多い組から順に並べ、等間隔にサブ系列に切って、「サブ系列内 or 自分の組内のみでアテンションする」といった感じです。それで組分けのルール locality sensitive hashing が肝心ですが、これは3ページ目の図でしょうか。点 x とその少し後ろにいる点 y があったとして、点 x をランダムに回転させたときに同じ色のエリアにいるか、といった絵にみえますが…後で実装をみてみましょう。
Linformer（Wang et al. 2020）	セルフアテンション内での射影の行列を低ランク近似することで $\mathcal{O}(L)$ を達成しているのですかね。しかし時系列の長期予測の場合は行列が固定できない故に $\mathcal{O}(L^2)$ まで劣化する可能性があるとありますが…？
Transformer-XL（Dai et al. 2019）	これらは「補助隠れ状態」を用いることで計算量を抑えつつ遠い過去の情報を利用できるようにしたようですが、であれば今回用いられたアプローチとは違いますね。これらのアプローチは時系列には応用できるのでしょうか…？

何にせよこれらでは「時系列の長期予測」という目的を達成するのに不十分といっているわけです。問題点の 1. の計算量にしか対処していないと。そもそも「LogSparse Transformer」を除いて時系列の予測を企図していませんし、「LogSparse Transformer」も長期予測を主眼においてはいないと思いますが。

問題点の 3. は長期予測に独特だからともかく、2. の必要メモリへの取り組みはあったんじゃないのかな。そのまま「蒸留BERT」なるモデルが公開されていて Linformer でも引用されているし、さらに「貧乏人のためのBERT」なんていう論文もあるよ。今回の手法とは枠組みが違うのかな？

BERT を動かせない人が貧乏なのではありません、BERT を動かせる計算資源を利用できる人がお金持ちなのです…。

モデル

気を取り直してモデルの詳細に入りましょう。まずモデルの入出力は、

モデルの入力は $d_x$ 次元ベクトルが $L_x$ 個並んだもの $\mathcal{X}^t = \{x_1^t, \cdots, x_{L_x}^t\}$ です。
モデルが出力すべきは $d_y$ 次元ベクトルが $L_y$ 個並んだもの $\mathcal{Y}^t = \{y_1^t, \cdots, y_{L_y}^t\}$ です。つまり、長期予測といっても、遠い未来の1点ではなく、遠い未来までのすべての点の予測を目指すということを含意していると思います。

そしてまず Self-Attention の話がありますね。Self-Attention の復習として下に絵を描いてみました。これは "I understand." という文章（ピリオドも1トークンとしさらに先頭トークンと末尾トークンを追加すれば5トークンからなる）を流したときのイメージで、アテンションの行列の数値は実際にこの文章を bert-large-cased 学習済みモデルに流して書き出したものです。であれば実際はヘッド数は16あるんですが面倒なので4ヘッドしか描いていません。bert-large-cased では入力特徴及び出力特徴の次元数は1024次元で、1ヘッドあたりが出力するのは64次元ですね。図中の $d=64$ ということです。

うん、自然言語処理では普通「文章長さ＜特徴次元数」だからその図の入出力みたいに横長の長方形になるわけだよね。でも今回は長期予測をしたいから、Table 1, Table 2 にある数値の単位がステップ数で合っているなら予測部分だけで960ステップ流したいことになるよね。BERTには256ステップ以上流せない設定になっているくらいだから、長いわけだね。計算量は流すステップの長さを $L$ とするなら $QK^\top$ の部分の行列積が $\mathcal{O}(L \cdot d \cdot L)$ で、最後のアテンションを適用するときの行列積が $\mathcal{O}(L \cdot L \cdot d)$ だから、 $d$ を定数扱いすれば $\mathcal{O}(L^2)$ だね。

ええまさにそのような話が続きます。なので計算量が $\mathcal{O}(L^2)$ になることを割けるべく、これまで Sparse Transformer や LogSparse Transformer は行列 ${\rm Softmax}(QK^\top /\sqrt{d})$ （面倒なのでこれ以降セルフアテンション行列とよびます）の成分を全て計算するのではなく間引きをやってきたわけですが、幾分ヒューリスティックな回避策であったわけです。それに、全ての Multi-Head で同じ間引き方をしていたと…そうなんですか？いやいわれてみれば Head ごとに間引き方を変えるべきですよね…。ともかく、現実にはセルフアテンション行列は疎であるということです。まあ特に自然言語処理では過去の単語たちをべったり注意することもないでしょうね。しかしどのように疎なのかがわからないから間引き方がわからないのですが…読み進めると3ページ目の2段目の最上部では、あるステップから各ステップをどれだけ注意するかの分布 $p$ と、一様分布 $q$ のKLダイバージェンスを取っていますね。なるほど一様分布から逸脱しているほど特定のステップに着目し、重要な情報を掴んでいる見込みが高いというわけでしょうか。以下の図でも計算してみました。

f:id:cookie-box:20210211142747p:plain:w520

上図の一番最後の式の第1項は定数なので無視して、第2項と第3項が式 (2) の $M(q_i, K)$ に相当しますね。論文中では sparsity measurement とよばれていますが、「ステップ $i$ からの各ステップへの注意分布の一様分布からの逸脱度」です（以下この記事中では逸脱度とよびましょう）。そしてセルフアテンション行列の各行のうち、逸脱度が高い $u$ 本のみを残すと。 $u$ を $\log L$ に比例させるようにとれば計算量は $\mathcal{O}(L \log L)$ になると…いやいやいや！そもそもセルフアテンション行列を得る計算量が $\mathcal{O}(L^2)$ なわけですよね？セルフアテンション行列が得られた上で「この $u$ 本だけ残そう」では意味がないですよね？？

続きを読もう。しかし逸脱度自体を得るのに $\mathcal{O}(L^2)$ かかってしまう、だから逸脱度を近似するというようにあるよ。まず補題1で逸脱度の上下限を示しているね。上下限がこうなるのは上図の式と見比べればわかる。それでこの上限の方を、完全なセルフアテンション行列からではなく、サンプリングした一部の要素だけ計算したセルフアテンション行列から見積もる。 $Q, K$ の分布の形にある程度の仮定をおけば、 $Q$ の行と $K^\top$ の列の組を $L \log L$ 組サンプリングすることで見積もれるって。そのことをきちんと示したのが命題1かな。 $k_j$ が正規分布にしたがうとしているのはどれくらい適切なのかわからないけど。まあ確かに分布が一様分布から離れているかって、分布の一番高いところが高かったらそれは離れているし、各行の最大値を見積もるだけなら行列の要素を全て計算しなくてもよさそうだよね。

サンプリングの仕方は追えていませんが、一様分布から離れているかどうかというのは、過去のヒューリスティックな回避策に比べれば積極的に意味のあるアテンションを残そうとしていますね。

セルフアテンションの計算量の問題が片付いたら次はメモリの問題でしたっけ。モデルサイズの問題といってもいいのでしょうか。セルフアテンション時の計算量を間引いても、セルフアテンション層をどんどん積み重ねるならパラメータ数とメモリ使用量は増えるばかりです。

その問題については論文4ページ目の Figure 3 をみるに、セルフアテンション層を抜ける度に Conv1D + MaxPool1D することで系列の長さを半分にしているようにみえるね。あ、この図では Attention Block という薄オレンジの直方体の中にガラス板（？）が4枚浮かんでいるようにみえるけど、これは4つのヘッドのセルフアテンション行列だね。式 (5) をみると Conv1D を適用した後に ELU で活性化している。

ELU — PyTorch 1.7.1 documentation

では最後はここまで改造した Transformer を用いてどのように推論するのかという問題ですか。1ステップずつ再帰的に読み出していくのでは時間がかかるというより誤差が積み重なっていくのですよね？

それについてはそのまま「1ステップで読み出すようにした」という感じにみえるな。以下にイメージ図を描いたよ。水色が目的変数でピンク色が説明変数（タイムスタンプなど）ね。本文中の例では、向こう7日分を予測するのに、デコーダにここまでの5日分をフィードするみたい。それで予測してほしい箇所はゼロにした状態（いわば「プレースホルダ」）を渡してそこに埋まるものを返してねって感じなんだけど、エンコーダに渡す期間とデコーダに渡す期間が把握できていないから、以下の図は GitHub の Informer の実装をみて描き直すかもしれないかな…。それで損失関数は MSE とあるね。検証したのは全部回帰タスクみたいだし。特に言及がないから、近い未来の誤差も遠い未来の誤差も重さは等しいということなのかな？

f:id:cookie-box:20210214014501p:plain:w290

検証データと比較手法

ではモデルについては一通り確認したので検証されたデータセットをみてみましょう。「電気」「電気」「天気」といったところでしょうか。

ETT (Electricity Transformer Temperature)	これは著者らが収集されたデータなのですね。以下に公開されているようです。 GitHub - zhouhaoyi/ETDataset: The Electricity Transformer dataset is collected to support the further investigation on the long sequence forecasting problem. Electricity Transformer Temperature という言葉が聞き慣れないですが、このデータセットは「変圧器の油温」を予測することを企図したものであるようです。よくわからないのですが、変圧器の油温というのが上昇しすぎると危険であって、変圧器に負荷がかからないように送電するために重要な指標ということなんでしょうか。説明変数には High UseFul Load などが含まれていますがこれは最大実効負荷などと訳すのでしょうか。ともかく、ETT-small-m1, ETT-small-m2 というのが中国のある2つの省の分単位のデータであって2年×365日×24時間×60分=1,051,200点のデータを含むそうです。時間単位になっている ETT-small-h1, ETT-small-h2 なるデータもあるようですね。
ECL (Electricity Consuming Load)	また電気ですが、お馴染みの UCI Machine Learning Repository のデータですね。 UCI Machine Learning Repository: ElectricityLoadDiagrams20112014 Data Set このデータは NeurIPS2018 の Deep State Space Models for Time Series Forecasting や NeurIPS2020 の AST でも利用されていました。ある期間におけるポルトガルの370人の個々の顧客の15分ごとの電力消費量です。
Weather	アメリカの1600地点での1時間毎の気候データでしょうか。論文中のリンクは以下に転記してみましたが、この記事をかいている時点で重すぎてアクセスできる気配がないのですよね…。 https://www.ncdc.noaa.gov/orders/qclcd/

そして比較対象となっている手法は以下です。

ARIMA	ARIMA は ARIMA ですね。ただ ARIMA の参考文献として以下が引用されているのは何故なんでしょうか。 (PDF) Stock price prediction using the ARIMA model
Prophet	Prophet も Prophet です。
LSTMa	LSTMa とは…？これは機械翻訳の論文のようですが、LSTM を普通に利用するのではなく、LSTM の各ステップの特徴を用いてデコードするコンフィギュレーションのことを LSTMa というのでしょうか。間違っていたらごめんなさい。
LSTnet	LSTnet は以下の論文を読んだときに引用されていましたね。絵も描きました。畳込みと再帰のハイブリッドモデルさんでしたね。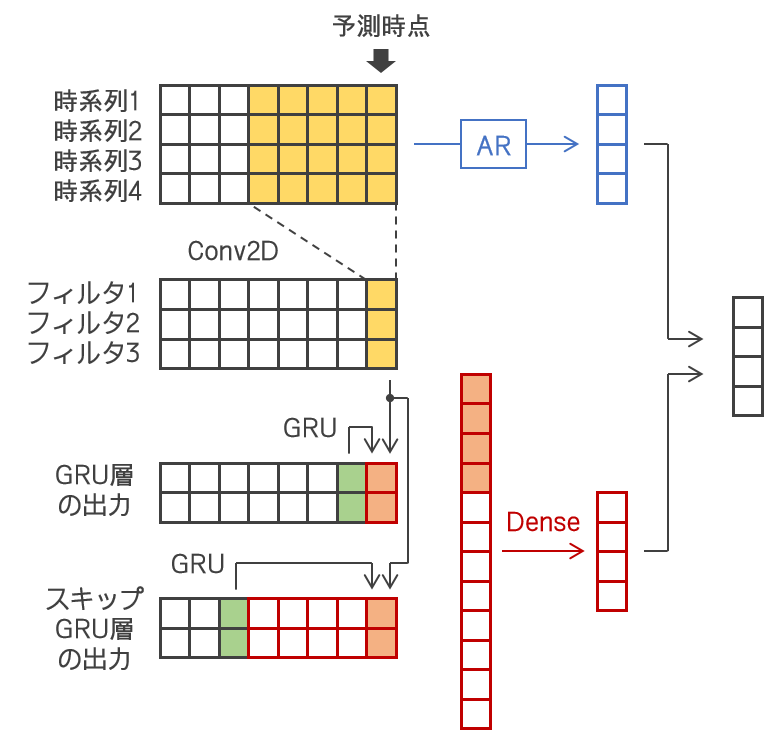論文読みメモ： Think Globally, Act Locally: A Deep Neural Network Approach to High-Dimensional Time Series Forecasting（その1） - クッキーの日記
DeepAR	DeepAR も DeepAR です。AST でも DeepAR の敵対的学習を試行されていましたね。ただ DeepAR は後続に Deep State Space Models があったと思いますがそちらは利用できないものなのでしょうか。

さらに、これらのモデルとは別に、「ProbSparse」によるセルフアテンションの有効性の検証として、今回のモデルのセルフアテンション部分のみを「通常のセルフアテンション」「Reformer のセルフアテンション」「LogSparse Transformer のセルフアテンション」に置き換えたモデルも比較対象にエントリーされています。公平を期すために、どのモデルのコンフィギュレーションも1GPUで推論可能なように調整されているようです（通常のセルフアテンションもなんでしょうか？）。

その結果が Table 1, Table2 ですね。ほとんどのタスクで Informer が最高精度を達成しています…って、通常のセルフアテンションよりも高精度が出ているタスクが多いのですね。Informer はセルフアテンション行列の計算を間引いたのに間引かないよりも性能がよいとはなぜなのでしょう？

取るに足らないアテンションなら最初から要らなかったということだよね。単変量予測の Table 1 で目立つのは ECL データの 48, 168, 336 ステップ先予測で DeepAR が健闘しているね。どうしてなんだろう？

私にいわれましても…。多変量予測の Table 2 もだいたい Informer 眷属の独断場ですがたまに LSTnet さんが健闘していますね。

Table 2 のモデルの中でさ、畳込みも再帰も利用しているのって LSTnet だけだよね。Transformer は特殊な畳込み扱いとして。逆に色々使っている LSTnet が少ししか勝てないのが Transformer の威力なんじゃないのかな。

私にいわれましても…。セルフアテンション手法の Reformer は精度が奮わないですね。時系列データと相性が悪いんでしょうか。Table 4 はセルフアテンション蒸留をしない場合の参考記録ですね。ハイフンになっている箇所はアウトオブメモリーと。フィードする入力系列の長さが同じならさすがに蒸留しない方が高精度は出ますが、如何せん入力系列の長さが食えないので結局蒸留した方がよい、といえそうです。Table 5 は再帰的にデコードした場合の結果で…再帰的なデコードでは誤差が大きすぎてもうお話にならなかったようですね。

一旦おわり

2021-01-31

雑記：分散共分散行列のベイズ更新の話

雑記

2021-02-02 絵を追加しました。

いろいろな場面（カルマンフィルタ、ガウス過程回帰など、直接観測できない何かの分布をその線形変換の観測からベイズ更新する場面）で以下の問が出てくると思います。

$x \in \mathbb{R}^n$ は確率ベクトルでその事前分布は平均 $0$ で分散共分散行列が $V \in \mathbb{R}^{n \times n}$ の多変量正規分布です。
$y \in \mathbb{R}^m$ も確率ベクトルで $y = Hx + w$ です。 $H \in \mathbb{R}^{m \times n}$ は行列です。 $w \in \mathbb{R}^m$ は平均 $0$ で分散共分散行列が $R \in \mathbb{R}^{m \times m}$ の多変量正規分布にしたがうノイズで $x$ とは独立です。
いまある $y$ が観測されました。この $y$ の下での（＝事後分布の） $x$ の分散共分散行列はどうなりますか？

普通はベイズの定理で $x$ の確率密度関数を考えると思います。

方法1．ベイズの定理で $x$ の確率密度関数をかく

$\begin{split} \displaystyle p(x|y) \propto p(y|x)p(x) &\propto \exp \left( -\frac{1}{2} (Hx)^\top R^{-1} Hx\right) \exp \left( -\frac{1}{2} x^\top V^{-1} x\right) \\ &= \exp \left( -\frac{1}{2} x^\top (V^{-1} + H^\top R^{-1} H) x\right) \end{split}$

より $x$ の事後分散共分散行列は $(V^{-1} + H^\top R^{-1} H)^{-1}$ である。

こうすると観測前は精度行列（分散共分散行列の逆行列で、多変量正規分布の密度関数の式で確率ベクトルに挟まれているやつ）が $V^{-1}$ だったのが観測後は $V^{-1} + H^\top R^{-1} H$ になっていて、精度が大きくなった（＝分散が小さくなった）感があります。観測の精度 $R^{-1}$ が大きいならより精度はより大きくなるし、 $H=0$ なら（観測が $x$ を反映しないなら）精度は全く大きくならないこともわかります。

別に以上でいいんですが、上の方法は終始 $x$ の精度の世界で考えていて、 $x$ の分散に何があったのかわかりにくいものになっています（？）。そもそも $y$ が観測されたら $x$ の分布がどうなるのかというのは $(x,y)$ の同時分布を考えるのが正攻法であるはずです（？）。なのでそれでやってみます。また、ここでは（※）の箇所で後述の補題を利用します（条件付き共分散をとる方法は色々あると思いますが、この補題は直接的に条件付き共分散はこれですというものなので利用しました。これは行列をブロック単位で UDL 分解するのと等価です）。

方法2． $(x,y)$ の同時分布を出してから $x$ の分散共分散行列を取り出す
多変量正規分布のモーメント母関数は $M_X(t) = E(e^{t^\top X}) = \exp \Bigl( \mu^\top t + \frac{1}{2} t^\top \Sigma t \Bigr)$ なので、 $(x,y)$ の同時分布のモーメント母関数は以下のようになる。

$\displaystyle \begin{split} E \left[ e^{ \left( \begin{array}{cc} t_1^{\top} & t_2^{\top} \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)} \right] &= E \left[ e^{ t_1^{\top} x + t_2^\top H x + t_2^\top w} \right]= E \left[ e^{ t_1^{\top} x + t_2^\top H x} \right] E \left[ e^{ t_2^\top w} \right] \\ &= \exp \Bigl( \frac{1}{2} t_2^\top R t_2 \Bigr) \exp \Bigl( \frac{1}{2} (t_1^\top + t_2^\top H) V (t_1 + H^\top t_2) \Bigr) \\ &= \exp \Bigl( \frac{1}{2} \left( t_1^\top V t_1 + t_1^\top V H^\top t_2 + t_2^\top H V t_1 + t_2^\top HVH^\top t_2 + t_2^\top R t_2 \right) \Bigr) \\ &= \exp \left( \frac{1}{2} \left( \begin{array}{cc} t_1^{\top} & t_2^{\top} \end{array} \right) \left( \begin{array}{cc} V & VH^\top \\ HV & HVH^\top + R \end{array} \right) \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right) \right) \end{split}$

よって $(x,y)$ の同時分布は分散共分散行列が $\displaystyle \tilde{V}_{x,y} = \left( \begin{array}{cc} V & VH^\top \\ HV & HVH^\top + R \end{array} \right)$ の多変量正規分布である。このとき $x$ の分散共分散行列 $\tilde{V}_{x}$ は $\tilde{V}_{x,y}$ の右下 $m \times m$ ブロックに対するシューア補行列（※）に他ならず、したがって $V - VH^\top (HVH^\top + R)^{-1} HV$ である。

こうすると観測前は分散が $V$ だったのが観測後は $V - VH^\top (HVH^\top + R)^{-1} HV$ になっていて分散が小さくなった感があります。（※）では以下の補題を利用しました（参考： Sherman-Morrison-Woodburyの公式 (Schur補行列) - いんふらけいようじょのえにっき）。

補題（シューア補行列）
正方行列 $P \in \mathbb{R}^{(n+m) \times (n+m)}$ を $A \in \mathbb{R}^{n \times n}, \, D \in \mathbb{R}^{m \times m}$ が正方行列になるように $\displaystyle P = \left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$ と区分けする。このとき $P$ も $D$ も正則ならば、 $S = A - BD^{-1}C$ も正則で $P^{-1}$ の左上 $n \times n$ ブロックは $S^{-1}$ になる。この $S$ を $P$ の $D$ に関するシューア補行列とよぶ。

証明は元の記事にありますが、記事中で示されているのは左上ブロックに対するシューア補行列の方なので、LDU 分解を UDL 分解に変更して右下ブロックに対するシューア補行列の方を示してください。同時共分散行列の LDU 分解には $y$ の共分散が陽にあらわれ、UDL 分解には $x$ の共分散が陽にあらわれます（以下）。なので $x$ の共分散がほしいときは UDL 分解するのが自然なはずです。上の補題は UDL 分解の $\tilde{X}$ が $A - BD^{-1}C$ であるといっているのと同じです。

LDU 分解すると以下の $Y$ が $y$ の共分散： $\displaystyle \left( \begin{array}{cc} t_1^\top & t_2^\top \end{array} \right) \left( \begin{array}{cc} I & O \\ W & I \end{array} \right) \left( \begin{array}{cc} X & O \\ O & Y \end{array} \right) \left( \begin{array}{cc} I & Z \\ O & I \end{array} \right) \left( \begin{array}{c} t_1^\top \\ t_2^\top \end{array} \right) = \left( \begin{array}{cc} t_1^\top + t_2^\top W & t_2^\top \end{array} \right) \left( \begin{array}{cc} X & O \\ O & Y \end{array} \right) \left( \begin{array}{c} t_1 + Z t_2 \\ t_2 \end{array} \right)$
UDL 分解すると以下の $\tilde{X}$ が $x$ の共分散： $\displaystyle \left( \begin{array}{cc} t_1^\top & t_2^\top \end{array} \right) \left( \begin{array}{cc} I & \tilde{Z} \\ O & I \end{array} \right) \left( \begin{array}{cc} \tilde{X} & O \\ O & \tilde{Y} \end{array} \right) \left( \begin{array}{cc} I & O \\ \tilde{W} & I \end{array} \right) \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right)= \left( \begin{array}{cc} t_1^\top & t_1^\top \tilde{Z} + t_2^\top \end{array} \right) \left( \begin{array}{cc} \tilde{X} & O \\ O & \tilde{Y} \end{array} \right) \left( \begin{array}{c} t_1 \\ \tilde{W}t_1 + t_2 \end{array} \right)$

なお、方法1．の結論は $(V^{-1} + H^\top R^{-1} H)^{-1}$ で、方法2．の結論は $V - VH^\top (HVH^\top + R)^{-1} HV$ で、なんか違ってみえますが、以下の Sherman-Morrison-Woodbury の公式よりこれらは等しいです。というかむしろ方法1．と方法2．で事後分散共分散行列を求めると Sherman-Morrison-Woodbury の公式が証明できることになります（まともな証明は先の記事にありますが、LDU 分解と UDL 分解の逆行列の成分比較によります）。

Sherman-Morrison-Woodbury の公式

$A \in \mathbb{R}^{n \times n}, \, B \in \mathbb{R}^{n \times m}, \, C \in \mathbb{R}^{m \times n}, \, D \in \mathbb{R}^{m \times m}$ について、 $A$ も $D - CA^{-1}B$ も $D$ も $A - BD^{-1}C$ も正則なとき、以下の恒等式が成り立つ。

$(A - BD^{-1}C)^{-1} = A^{-1} + A^{-1} B (D - CA^{-1}B)^{-1} C A^{-1}$

では $(V^{-1} + H^\top R^{-1} H)^{-1}$ と $V - VH^\top (HVH^\top + R)^{-1} HV$ のどちらの表現が便利なのかというと、逆行列が取られている行列が前者は $n \times n$ 、後者は $m \times m$ なので、 $m$ が大きければ前者、 $n$ が大きければ後者が逆行列の計算コストが低いはずです（なので推定対象の状態空間が高次元の場合は方法1．で前者を求めてから Woodbury の公式で後者にしましょうとかいわれると思います）。

それで、どうして方法1．と方法2．で逆行列をとる行列のサイズに違いが出てくるのか気になるわけですが、トートロジカルですがどこの行列が正則であることを利用しているかが違うはずです。

方法1．：ベイズの定理を使う場合だと、終始「密度の積（精度の和）」で考えるので逆行列を取るのは最後の仕上げになり、 $x$ の精度行列＝ $n \times n$ 行列の逆行列をとることになります。
方法2．：同時分布の分散共分散行列を出してから補題（シューア補行列）を利用する場合だと、この操作で直接利用するのは同時共分散行列の右下ブロックが正則であることです。
- シューア補行列 $S$ が存在するならば $S = A - BD^{-1}C$ であることを示すときに利用するのは $D$ が正則であることだけです。
- なお、同時共分散行列の LDU 分解の $P^{-1}$ と成分比較することもできます。この場合は左上 $n \times n$ ブロックの $A$ が正則であることを利用することになり、また、出てくる答えが方法1．と同じになります（方法2．の $\tilde{V}_{x,y}$ の各ブロックを $A^{-1}+A^{-1}B(D - CA^{-1}B)^{-1} CA^{-1}$ に代入）。なので、同時共分散行列を経由することではなく、そこから如何に $x$ の共分散行列をとるかが逆行列のサイズを決めています。

方法1．

「 $x$ の事前共分散行列」
　↓　ベイズの定理
「 $x$ の事後精度行列」
　↓　逆行列 ― 精度行列全体 $n \times n$ が正則であることを利用
「 $x$ の事後共分散行列」

方法2．

「 $x$ の事前共分散行列」
　↓　 $(x,y)$ の同時分布のモーメント母関数
「 $(x,y)$ の同時共分散行列」
　↓　補題（シューア補行列）― 同時共分散行列の右下 $m \times m$ ブロックが正則であることを利用
「 $x$ の事後共分散行列」

まとめると（まとめではない）、 $(x, y)$ の同時共分散行列を $P$ とおくとベイズの定理は精度行列 $P^{-1}$ の UDL 分解（ $P$ の LDU 分解）の左上ブロックをとることに他ならず、それに Woodbury の公式を適用すると $P^{-1}$ の LDU 分解（ $P$ の UDL 分解）の左上ブロックになるので正則を仮定するブロックが左上から右下に切り替わる、という感じがします（無論ベイズ更新の文脈ではどちらも正則でないと困るのですが正則であることを明示的に利用するのがどちらなのかが切り替わる）。

2021-02-02 追記

絵を描きました。スタートから出発してゴールを目指します。★は逆行列の操作なので大きな逆行列はなるべく避けます。ただし図は $n > m$ のイメージで描いています。この大小関係によって適切なルートを選びます。

f:id:cookie-box:20210202184504p:plain

2021-01-30

GPML：ノート1（1章、2.1節）

本読み

以下の本を読みます。私の誤りは私に帰属します。お気付きの点がありましたらご指摘いただけますと幸いです。

www.gaussianprocess.org

キャラクターの原作とは無関係です。

f:id:cookie-box:20180305232608p:plain:w60

「訓練データ $\mathcal{D} = \bigl\{ (x_i, y_i), \cdots, (x_n, y_n)\bigr\}$ から任意の未知の点 $x$ の値をどう予測すればよいか」という問を考えましょう。本質的に有限個の点の情報から無限個の点の情報を得ることはできません。考える関数 $f(x)$ が訓練データの外でどうあるべきかについて僕たちは何も知らない。無限にある関数候補に優劣を付けられない。なのでそこは何か決め打つしかない。それには主に2つのアプローチがあるといっています。

考慮するべき関数のクラスを制限する。
すべての関数に事前確率を割り当てる（Ex. より滑らかなものが好ましいなど）。

実際に用いられる方法は 1. の関数のクラスを制限することでしょう。テキストでは例えば線形モデルといっていますが、特定の構造のニューラルネットや決定木のことも多いかもしれません。その予め決めたクラスの関数の中で訓練データに最もフィットするものを選ぶわけですが、この方法では表現力が不十分だと予測性能が悪くなり、といって表現力をもたせると訓練データにオーバーフィットするとあります。

なので 2. が実現できないかという流れなのでしょう。こちらで関数のクラスを制限することは避けたい、ただある程度滑らかであることだけ要請しておきたい、と。しかし、こちらには即座にセルフ突っ込みが入っていますね。「有限の時間でどうやって無限の関数候補を検討するんだ」と。

―そこで、「ガウス過程が助けにきてくれる」と、ガウス過程が初登場します。

f:id:cookie-box:20180305231302p:plain:w60

ごめん、「助けにきてくれる」っていわれても、意味がわからなすぎて「熱い展開！」とか「これで勝てる！」とかならない…。

そうですね、まだイントロダクションなので続く記述はいくぶん抽象的ですが、ガウス過程があると助かるという心は以下だと思います。この箇所にかいていないことも適当に想像でかきましたが。

訓練データ外のことはわからないので、あらゆる関数の上の確率分布（＝確率過程）を考えたい。
ここでその確率過程はガウス過程であることを仮定する。そうすれば、距離が近い点どうしは共分散が大きいような分散共分散行列を選ぶことで、滑らかな関数の事前確率を大きくすることができる。そして、未知の点上の値の分布は直接求まるので、無限の関数候補を個々に検討する必要はない。

何というか、2. のアプローチは未知の点を予測するのに「あるクラスの関数の中から尤もらしいものを特定する」ことによってそうするのではなく、「点どうしに相関関係を入れる」ことによってそうするというとしっくりくる気がします。ここではそれを「すべての関数に事前確率を割り当てる（滑らかな関数の事前確率が大きいような）」といっていますが。

3ページから4ページの前半は Figure 1.1 で1次元→1次元の回帰のデモンストレーションをしていますね。(a) の事前分布が、2点を観測すると (b) の事後分布になると。そして4ページの中ほどにはまさに「ガウス過程回帰するとは共分散を見出すことである」というような記述があります。

4ページの後半からは分類問題ならどうかという話ですね。座標 $x$ に検出された天体が星であるのか銀河であるのかを分類したいというシチュエーションのようです。座標 $x$ の天体が星である確率 $\pi(x) \in [0,1]$ を予測したいと。しかし、ガウス過程のある座標での実現値は $[0,1]$ には収まりませんから、ロジスティック関数で変換するのが常套手段であるようですね。2次元平面上でのこの2値分類の事後分布が Figure 1.2 の (d) です。

後はこの本の章立てが紹介されていますね。各章の内容は概して以下でしょうか。

ガウス過程の定義や、回帰問題の予測値の計算方法（ノイズがガウシアンなら解析的）。
2値/多値分類問題（非線形な活性化関数を用いるためにもはや解析的でない）。
様々な共分散関数とその性質、組み合わせ方。
共分散関数のパラメータ推定方法。
ガウス過程回帰はカーネルマシンの1手法に位置付けられるが、SVMなど他のカーネルマシンの紹介と、ガウス過程回帰との関係。
理論的な話（漸近理論や、学習曲線や、PACベイズ推測の枠組みについて）。
$n \times n$ 行列の逆行列への対処法。
その他の問題設定。

じゃあまずはともかく Chapter 2 の「回帰」だな…序文に「ガウス過程モデルの解釈は色々ある」ってあるな。このテキストで扱うのは「関数空間」派と「重み空間」派ってことかな？とりあえず後者を先にみていくのか。えっと、訓練データが $\mathcal{D} = \bigl\{ (x_i, y_i), \cdots, (x_n, y_n)\bigr\}$ であるのは変わらなくて、入力は $D$ 次元、出力は1次元の実数で、入力ベクトルを束ねた $D \times n$ 行列 $X$ を計画行列とよぶと（これの転置を計画行列とする流儀の方が多いけど意図的に）。そしていまの状況は入力が与えられた下での出力の分布に興味がある（入力の分布自体には興味がない）のか。

それでまず、 $y=f(x)+\varepsilon, \; f(x) = x^\top w, \; \varepsilon \sim N(0, \sigma_n^2)$ というモデルを考えるのかな。これは入力の線形和に分散 $\sigma_n^2$ の独立なガウスノイズがのっているというモデルか。そうすると訓練データに対するモデルの尤度 $p(y|X,w)$ は式 (2.3) になって、 $w$ の事前分布を $w \sim N(0,\Sigma_p)$ として事後分布を求めるのかな？それがなんで式 (2.5) になるんだっけ？

式から $X$ による条件付けの部分を取った方がわかりやすいかもしれません。

$\displaystyle p(w|y)= \frac{p(y|w)p(w)}{p(y)}$

これなら $p(y|w)p(w)=p(w|y)p(y)$ を変形しただけですね。しかしいま考えているモデルは $w$ のみから $y$ を出すモデルではありませんから、 $X$ による条件付けを入れましょう。

$\displaystyle p(w|y, X)= \frac{p(y|w, X)p(w|X)}{p(y|X)}$

ここで $w$ の事前分布は計画行列 $X$ に応じて決めているのではないので $p(w|X)=p(w)$ とするだけです。それでは実際に事後分布を求めておきましょうか。

$\begin{split} \displaystyle p(w|X, y) &\propto \exp \left[-\frac{(y - X^\top w)^\top (y - X^\top w)}{2\sigma_n^2} - \frac{w^\top \Sigma_p^{-1} w}{2} \right] \\ &\propto \exp \left[-\frac{- y^\top X^\top w - w^\top X y + w^\top X X^\top w}{2\sigma_n^2} - \frac{w^\top \Sigma_p^{-1} w}{2} \right] \end{split}$

よって、これは以下の形に平方完成できますから、係数比較で $\bar{w}$ を求めましょう。

$\begin{split} \displaystyle & \exp \left[-\frac{1}{2}(w - \bar{w})^\top \left( \frac{X X^\top}{\sigma_n^2} + \Sigma_p^{-1} \right) (w - \bar{w}) \right]\\ &\propto \exp \left[-\frac{1}{2}w^\top \left( \frac{X X^\top}{\sigma_n^2} + \Sigma_p^{-1} \right) w +\frac{1}{2} \bar{w}^\top \left( \frac{X X^\top}{\sigma_n^2} + \Sigma_p^{-1} \right) w +\frac{1}{2} w^\top \left( \frac{X X^\top}{\sigma_n^2} + \Sigma_p^{-1} \right) \bar{w}\right] \end{split}$

見比べると $\bar{w} = \sigma_n^{-2}(\sigma_n^{-2} X X^\top +\Sigma_p^{-1} )^{-1}Xy$ であることがわかりますね。つまり、事後分布は平均が $\bar{w}$ で分散共分散行列が $(\sigma_n^{-2} X X^\top +\Sigma_p^{-1} )^{-1}$ のガウス分布です。ときにハヤト、線形モデル $f(x) = x^\top w$ を最小2乗フィッティングしたときの $\hat{w}$ ってどうなりましたっけ。

それは $\hat{w} = (X X^\top)^{-1}Xy$ だろ（下スライド）。リッジ正則化するなら $\hat{w} = (X X^\top + \lambda I)^{-1}Xy$ だっけ。あれ？これって $\bar{w}$ とすごい似てる？

似ているが混同するなと 10 ページにあります。

ええ…じゃあ訊くなよ…。

$\hat{w}$ はペナルティ項付きの尤度を最大にする $w$ であり、リッジ回帰の最終的な答えともいうべきものでしょう。他方、 $\bar{w}$ はベイズ推測の事後分布の平均であり最大点ですが、それだけなんです。事後分布の特徴的な点ではあるがこの点での予測値が特別な役割をもつのではないといいたいようです。このケースではたまたまモデルも事後分布も対称なので予測値の分布の平均値が $\bar{w}$ による予測値と一致するんですが。…続く 11 ページにも「未知の点を予測するときは、すべてのありうるパラメータでの予測値を事後分布による重みで平均します」とありますから、ベイズ推測とはあくまでそういうもので、事後分布のある点での予測値を使用するものではないということなのかと。しかし、渡辺ベイズ本の1章にも事後確率最大化推測とか平均プラグイン推測とかありましたから「特別な役割をもたせる人もいるのでは」となりそうなんですが、あくまで「ベイズ推測」というとそういうことではないということなのかもしれません。

ふーん…？まあ何にせよ、未知の点 $x_\ast$ に対する予測値 $f_\ast$ の分布は (2.9) 式で…何でこうなるんだっけ？

渡辺ベイズ本 1.2.3 節の「計算できる例」を参照すれば計算できるでしょう。計算できるわけですから。

あー…事前分布から事後分布への変換がハイパーパラメータの更新で表せるのをつかうんだっけか。それで、今回の場合は予測値の分布はガウス分布で、その平均は $x_\ast^\top \bar{w}$ で分散は $x_\ast^\top (\sigma_n^{-2} X X^\top +\Sigma_p^{-1} )^{-1} x_\ast$ になるのか。ん？「予測値の不確かさは入力の大きさが大きくなるほど大きくなり、これは線形モデルに期待する性質と合致している」みたいにあるけど、どういう意味？そんなこと線形モデルに期待してたっけ？

線形モデル $f(x) = x^\top w$ は $w$ が不確かなわけですから、 $f(x)$ の不確かさはノルムが大きい $x$ ではそれに比例して大きいだろうということなんでしょうか。今回考えた「入力の線形和に分散決め打ちのガウスノイズをのせるモデルを考え、重みベクトルをベイズ更新する」という方針ではそれが満たされていますね、というくらいでは。

まあいいや。Figure 2.1 にこの推測の図示があって、図 (a) の等高線が事前分布で、図 (b) が訓練データで（3点だけなんだな）、図 (c) の等高線は尤度で、図 (d) の等高線は事後分布で、図 (b) に戻って実線と点線が予測分布の信頼区間って感じか。図のキャプションをみると、図 (a)(c)(d) の等高線は1シグマ、2シグマで、図 (b) の破線は2シグマか。というか図 (c) と図 (d) めっちゃ似てるな。

事前分布がかかっているかどうかの違いしかありませんから、それは似ているでしょう。図 (c)(d) で特筆すべきなのは、図 (c) で切片の不確かさはまだ大きいのに対し傾きの不確かさはずっと小さいこと、図 (d) では傾きの広がりは図 (c) とほぼ変わらないのに対し切片は平均も分散も図 (c) からやや変わっていることですね（とキャプションにあるんですが）。この例では切片より傾きがずっとよく特定されます。図 (b) の直線について、切片を 0.5 増やしたときの尤度の減り方と傾きを 0.5 増やしたときの尤度の減り方を想像すればこれはわかるでしょう。

ちなみにプロデューサーさんが Figure 2.1 を再現しました（gist）。

f:id:cookie-box:20210130162410p:plain:w590

暇か。

ただもちろん線形モデルでは表現力が乏しいので、簡単に表現力をもたせる手法として入力 $x$ を基底関数 $\phi(x)$ で適当な高次元空間に送ればよい、と続く 2.1.2 節にありますね。 $\phi(x) = (1, x, x^2, x^3)^\top$ などとしてしまえばいいわけです。後の方の5章ではこの基底関数をどのように選ぶべきかという話題が出てくるようですが、さしあたり適当な基底関数が既に手に入っているものとします。いまや計画行列は $N \times n$ 行列 $\Phi = \Phi(X)$ となり、モデルは $f(x) = \phi(x)^\top w$ となりました。予測分布はどうなりますか？

どうなるって、 $X$ が $\Phi$ になるだけだよな。平均が $\phi(x_\ast)^\top \sigma_n^{-2}(\sigma_n^{-2} \Phi \Phi^\top +\Sigma_p^{-1} )^{-1} \Phi y$ で分散共分散行列が $\phi(x_\ast)^\top (\sigma_n^{-2} \Phi \Phi^\top +\Sigma_p^{-1} )^{-1} \phi(x_\ast)$ のガウス分布なんじゃ。

ええしかし、 $N \times N$ 行列 $\sigma_n^{-2} \Phi \Phi^\top +\Sigma_p^{-1}$ の逆行列を求めなければならないのがネックです。より表現力の高い基底関数を利用しようとするほど $N$ は大きいはずですし。

そうかもだけど仕方ないだろ。

思い出してください。多変量正規分布の積を平方完成した多変量正規分布の分散共分散行列を計算するときに工夫したことがありませんでしたか？

雑記： Schur 補行列と Sherman-Morrison-Woodbury の公式とカルマンフィルタとガウス過程回帰の整理 - クッキーの日記

そんなことやった覚えな…うわあやってる。

以下を今回の場合にあてはめてみましょう。

以下のサイズの行列 $A, \, B, \, C, \, D$ があるとき、
$A \in \mathbb{R}^{n \times n}, \quad B \in \mathbb{R}^{n \times m}$
$C \in \mathbb{R}^{m \times n}, \quad D \in \mathbb{R}^{m \times m}$ 以下の恒等式で逆行列がとられている行列に逆行列が存在するならば、以下の恒等式が成り立ちます。 $(A + BDC)^{-1} = A^{-1}-A^{-1}B(D^{-1}+CA^{-1}B)^{-1}CA^{-1}$ これを Sherman-Morrison-Woodbury の公式といいます。

	カルマンフィルタのフィルタ操作	線形基底関数モデルのベイズ推定
更新する分布	現在の観測に基づいて状態 $x_t$ の分布を前ステップでの一期先予測から更新したい	訓練データに基づいてパラメータ $w$ の分布を事前分布から事後分布に更新したい
$(A + BDC)^{-1}$	フィルタ分布の分散共分散行列 $({V_{t\|t-1}}^{-1} + {H_t}^{\top} {R_t}^{-1} H_t)^{-1}$ $= V_{t\|t-1}$ $\quad - V_{t\|t-1} {H_t}^{\top} (H_t V_{t\|t-1} {H_t}^{\top} + R_t)^{-1} H_t V_{t\|t-1}$	事後分布の分散共分散行列 $(\Sigma_p^{-1} + \sigma_n^{-2} \Phi \Phi^\top)^{-1}$ $= \Sigma_p$ $\quad - \Sigma_p \Phi (\Phi^\top \Sigma_p \Phi + \sigma_n^{2} I)^{-1} \Phi^\top \Sigma_p$
$A$	前回の一期先予測の分散共分散行列の逆行列 ${V_{t\|t-1}}^{-1}$	事前分布の分散共分散行列の逆行列 $\Sigma_p^{-1}$
$B = C^\top$	システムの転置 ${H_t}^{\top}$	計画行列 $\Phi$
$D$	観測ノイズの分散共分散行列の逆行列 ${R_t}^{-1}$	モデルの分散共分散行列の逆行列 $\sigma_n^{-2} I$

なので $n \times n$ 行列の逆行列を求めるので済むようになるわけです。 $n$ もデータ数なので大きいイメージがありますが、それより $N$ がずっと大きいケースを想定しています。こうしてみると、計画行列 $\Phi$ はパラメータ $w$ の側からみれば自分を $y$ に変換してくれるシステムなんですね。

というわけで改めて予測分布の分散共分散行列をかき直すとこうです。教科書に倣って $K = \Phi^\top \Sigma_p \Phi$ としました。

$\begin{split} \phi(x_\ast)^\top (\sigma_n^{-2} \Phi \Phi^\top +\Sigma_p^{-1} )^{-1} \phi(x_\ast) &= \phi(x_\ast)^\top \Sigma_p \phi(x_\ast) -\phi(x_\ast)^\top \Sigma_p \Phi (\Phi^\top \Sigma_p \Phi + \sigma_n^{2} I)^{-1} \Phi^\top \Sigma_p \phi(x_\ast) \\ &= \phi(x_\ast)^\top \Sigma_p \phi(x_\ast) -\phi(x_\ast)^\top \Sigma_p \Phi (K + \sigma_n^{2} I)^{-1} \Phi^\top \Sigma_p \phi(x_\ast) \end{split}$ それで、予測分布の平均については Sherman-Morrison-Woodbury の公式は要りませんでした。逆行列の前後に付いているのを逆行列の中に押し込めてみましょう。初手で $\Phi \Phi^\top$ を破壊できるんですよね。そもそも $(A + BDC)^{-1}$ の $BDC$ の部分が邪魔で崩したくて Woodbury の公式を使おうとなるんですが、勝手に崩れました。 $\begin{split} \phi(x_\ast)^\top \sigma_n^{-2}(\sigma_n^{-2} \Phi \Phi^\top +\Sigma_p^{-1} )^{-1} \Phi y &= \phi(x_\ast)^\top (\Phi^\top +\sigma_n^{2} \Phi^{-1} \Sigma_p^{-1} )^{-1} y \\ &= \phi(x_\ast)^\top ( (\Phi^\top \Sigma_p +\sigma_n^{2} \Phi^{-1}) \Sigma_p^{-1} )^{-1} y \\ &= \phi(x_\ast)^\top ( (K +\sigma_n^{2}I ) \Phi^{-1} \Sigma_p^{-1})^{-1} y \\ &= \phi(x_\ast)^\top \Sigma_p \Phi ( K +\sigma_n^{2}I )^{-1} y \end{split}$ なので、元より逆行列の中身が $n \times n$ 行列で済んでいます。

つづいたらつづく

2021-01-04

雑記：モデルをアンサンブルしたい話（その2―カステラ本7.11節、8.2節、8.4節、8.8節、10.1～10.4節）

雑記

私の誤りは私に帰属します。お気付きの点がありましたらお手数ですがご指摘いただけますと幸いです。

テキスト（カステラ本）

統計的学習の基礎 ―データマイニング・推論・予測― | Trevor Hastie, Robert Tibshirani, Jerome Friedman, 杉山将, 井手剛, 神嶌敏弘, 栗田多喜夫, 前田英作, 井尻善久, 岩田具治, 金森敬文, 兼村厚範, 烏山昌幸, 河原吉伸, 木村昭悟, 小西嘉典, 酒井智弥, 鈴木大慈, 竹内一郎, 玉木徹, 出口大輔, 冨岡亮太, 波部斉, 前田新一, 持橋大地, 山田誠 |本 | 通販 | Amazon の 256～257, 326～327ページ。

関連記事

まとめ（解釈を含む）

並行世界の自分が学習したモデルを取り寄せればバリアンスを小さくできる。が、そんなことはできないので自分で並行世界をつくり出す方法がブートストラップ法である（そのモデルたちを平均するのがバギングである）。
カテゴリ値を取るデータの標本 $Z$ からのノンパラメトリックブートストラップ標本は、「標本 $Z$ に対して、 $Z$ 内の各カテゴリの割合を生成したディリクレ分布をベイズ推定して、各カテゴリの割合がその事後分布に（ほぼ）したがうように標本をサンプリングする」ことをしたものであるといえる。ことから、バギングしたモデルは近似的にモデルのベイズ事後分布の平均であるとみなせる（ので普通に訓練したモデル＝MAP推定より2乗誤差が小さくなることが見込める）。
もっともベイズ事後平均を取るのであれば、異なるモデルたちを候補にしてもよい。そのときモデルを足し合わせる重みはBIC（「どのモデルがこの訓練データに対して最も尤もらしいか」という指標だった）を用いてもよいし、直接最適な重みを推定してもよい（スタッキング）。
そもそも足し合わせる各モデルが同じ標本を学ばなくてもよい。1つ前のモデルが誤分類したデータを重点的に学んでいくのがブースティング法の最も基本的なアルゴリズムであるアダブーストM1である。アダブーストM1は前向き段階的加法的モデリングにおいて指数損失を採用しても導出される。というより、前向き段階的加法的モデリングを解く手法全般をブースティングという。

キャラクターの原作とは無関係です。

前回は「並行世界の自分が学習したモデルを取り寄せればバリアンスを小さくできる。が、そんなことはできないので自分で並行世界をつくり出す方法がブートストラップ法である」というところまででしたね。

だいぶブートストラップ法に対する語弊がないかそれ…。そもそもブートストラップ法って何？自分で並行世界をつくるなんてことしていいの？

テキストでブートストラップ法が最初に出てくるのは286ページの7.11節ですね。前回もいった通りここでのブートストラップ標本とは「訓練データ $Z = \bigl\{ (x_1, y_1), \cdots, (x_N, y_N)\bigr\}$ から $N$ 点を復元抽出する」ことを $B$ 回繰り返して $B$ セットの新しい標本 $Z^{\ast 1}, Z^{\ast 2}, \cdots, Z^{\ast B}$ を得たものです。復元抽出なので元の訓練データの点はある $Z^{\ast b}$ に複数回抽出されていることもありますし、1回も抽出されていないこともあります。カギカッコ内は「訓練データの経験分布から $N$ 点生成する」といっても同じですね。なお、これはあくまでノンパラメトリックブートストラップといわれる方法であって、ブートストラップ標本を得る方法は他にも色々あります（テキスト302ページのノイズを添加する方法など）。より一般に、訓練データ自体を用いて並行世界たちの訓練データを複製する方法であればブートストラップ法のようです。そもそもブートストラップとは靴の後部の小さなつまみのことで、"pull oneself up by one's bootstraps" という慣用句で「他人の助けを借りずに自力で達成する」という意味であるようです。ので、この訓練データだけから新たな標本を生成する方法がブートストラップ法と名付けられたのでしょう。初出は1979年とか。

そういう手法なので、期待値や分散や信頼区間のモンテカルロ推定に利用されるのがメインなのではないでしょうか。7.11節に出てくるブートストラップ法の用法は以下ですね。汎化誤差の期待値の推定は込み入っています。ブートストラップ標本は元の標本の点を全ては含んでいませんから、そのディスアドバンテージ分をどう補ってやるかということになってくるようですね。

訓練データから計算される何らかの量 $S(Z)$ の分散を推定するのに、 $B$ 個のブートストラップ標本上の不偏分散でもって推定値とする。
汎化誤差を推定するのに、 $B$ 個のブートストラップ標本で学習したモデル $\hat{f}^{\ast 1}, \cdots, \hat{f}^{\ast B}$ による平均予測誤差の、全訓練データの平均を推定値 $\widehat{\rm Err}^{(1)}$ とする。なお、各 $x_i$ の平均予測誤差を出す際、点 $x_i$ を訓練データとして参照したモデルはとばす。また、この推定値には亜種がある（以下）。

上の推定値では、「個々の $\hat{f}^{\ast 1}, \cdots, \hat{f}^{\ast B}$ は本来の約63.2%のデータしか学べていない（ので汎化誤差を過大評価しているかもしれない）」という問題点がある。これを緩和するために、訓練誤差を36.8%混ぜる（このようになる導出はあるらしい）。これを $\widehat{\rm Err}^{(0.632)}$ とする。
上の推定値でも、「過学習のために訓練誤差が小さくなりすぎているかもしれない（ので訓練誤差を混ぜると逆に過小評価になるかもしれない）」という問題点がある。そこで、「相対過学習率」を、「 $\widehat{\rm Err}^{(1)}$ から訓練誤差を引いたもの」を「でたらめな正解ラベルを付けたときのそのモデルの予測誤差から訓練誤差を引いたもの」で割ったものとして定義する。「相対過学習率」が大きいほど $\widehat{\rm Err}^{(1)}$ を信用する。これを $\widehat{\rm Err}^{(0.632+)}$ とする。

ブートストラップ標本は元の標本の点を全ては含んでいないというのに関連して、元の標本が $N$ 点であったときにあるブートストラップ標本にある点が選ばれる確率は以下ですね。

def arutenga_erabareru_kakuritsu(N):
    p = 1.0 - 1.0 / float(N)  # 1回の抽出で自分以外の点が選ばれる
    p_total = 1.0  # N回の抽出すべてで自分以外の点が選ばれる
    for i in range(N):
        p_total *= p
    return 1.0 - p_total

ある点が選ばれない確率は $N = 1$ で $0$ 、 $N = 2$ で $0.25$ で、 $N \to \infty$ の極限でネイピア数の逆数になります。 $N' = -N$ とおけば $(1-1/N)^N = [ (1+1/{N'})^{-N'} ]^{-1} \xrightarrow[-N' \to - \infty ]{} e^{-1}$ ですから。
ただ7.11節にブートストラップ標本によって推定することがどのように正当かという記述はありませんね。そのような話題は8章にあるようです。以下にまとめます。文字の定義はテキストを参照してください。

真の値のノイズが加法的でガウシアンなときに、パラメトリックブートストラップ標本で学習したモデルの期待値が最尤推定の結果と一致する（8.2節）。
ガウス分布 $N(\theta, 1)$ の期待値 $\theta$ をベイズ推定する状況（ $\theta$ の事前分布も事後分布もガウス分布）では、事前分布の分散を無限大にすると（無情報事前分布）、ある点 $z$ を観測したときの事後分布が $N(z,1)$ となるが、パラメトリックブートストラップ標本はこの事後分布から1点 $\theta'$ をサンプリングして $N(\theta', 1)$ を得てそれの期待値を採用したものとみなせる（8.4節）。

つまり、パラメトリックブートストラップ標本は、「各点 $z$ に対して、 $z$ を生み出したのは $N(z,1)$ なんだろうなとベイズ推測して、その分布から点をサンプリングする」ことを各点に対してしたものであるといえる。

カテゴリ数が $L$ のカテゴリカルなデータの標本を得たとする。各カテゴリが生成される割合 $w$ の事前分布をすべてのカテゴリの集中度母数が0の極限のディリクレ分布とすると、事後分布はすべてのカテゴリの集中度母数が標本内での観測数であるディリクレ分布となるが、ノンパラメトリックブートストラップ標本内の各カテゴリの割合がしたがう分布（標本内の観測割合を母数にもつ多項分布）はこれに近い（平均が等しく分散共分散がほぼ等しい）（8.4節）。

つまり、ノンパラメトリックブートストラップ標本は、「標本 $Z$ に対して、 $Z$ 内の各カテゴリの割合を生み出したのは ${\rm Dir} (N \hat{w})$ なんだろうなとベイズ推測して、各カテゴリの割合がその分布にほぼ近くなる方法で標本をサンプリングする」ことをしたものであるといえる。

文字に色を付けた部分の気持ちになれば、天下りでなく演繹的にブートストラップ法にたどり着けるような気がするかもしれません。僕はしませんが。

しないのかよ！？あと、「ほぼ等しい」ってなんか中途半端じゃない？どれくらい等しいの？？

テキストにそうかいてあるものはかいてありますから…まあ確かめますか。 ${\rm Dir} (N \hat{w})$ にしたがう $\tilde{w}$ の分散は $\hat{w}_i (1 - \hat{w}_i) / (N + 1)$ で、 $N$ 倍が ${\rm Multi}(N, \hat{w})$ にしたがう $\tilde{w}$ の分散は $\hat{w}_i (1 - \hat{w}_i) / N$ ですから近いですね。共分散は $-\hat{w}_i \hat{w}_j / (N + 1)$ と $-\hat{w}_i \hat{w}_j / N$ なので近いです。

確かに近いな。じゃあこの状況でのブートストラップ法はほぼベイズ推定なんだ。

はい、テキスト8.8節「モデルの平均と統合」の冒頭にも「バギングしたモデルは近似的なベイズ事後平均になっていることがわかる」のような文があります。対して、普通に訓練したモデルはベイズ事後分布の最頻値をとっていることに対応すると。そして、2乗誤差に対して最適なのはベイズ事後平均です。ということからも、バギングすることで2乗誤差を小さくできることが見込まれます。これが一応の「自分で並行世界をつくるなんてことをしていいのか」に対する答えになるのではないかと。

そういわれるとそうなのか。

さらに8.8節では「平均する個々のモデルを異なるモデルにしたらどうだろうか」という議論を巡らせています。どう思いますか？

えっ、そんな、別々のモデルにしちゃったら、モデルたちはベイズ事後分布をなさないよな…「並行世界の自分にモデルをもらったけど並行世界の自分が学習したのは違うモデルだった」ってなったら、自分のモデルとどっちが尤もらしいかってわからないわけだし…それじゃ平均したら駄目なんじゃないの？

ええ、どちらが尤もらしいかわかりませんね。でも、前々回に、「どのモデルがこの訓練データに対して最も尤もらしい？」という指標を取り扱いませんでしたか？

あ、BIC…。

はい、そのような場合は BIC が利用できるとあります。また、より直接的に、「どのモデルにどれだけ重みを割り振れば誤差が最も小さくなる？」と重みを最適化するのが331ページ下部で紹介されているスタッキングです。ここで、モデル $m$ の $i$ 番目のデータに対する誤差の計算時には $i$ 番目のデータのみを除いた訓練データで学習したモデル $m$ を用意し、それで予測します。明確に記述されていませんが、データ数×モデル数だけ学習することになるので、結構面倒そうな気はします。

それで、バギングの重要例であるランダムフォレストは15章で掘り下げられています（ただ、ランダムフォレストでは決定木の分岐点を決めるときに特徴量もランダムに絞り込んでさらにバリアンスを下げる工夫をしているのでバギングというのかバギングの改造版というのかわかりませんが）。

さておき、ここまでで、「モデルを平均するとよい」「異なるモデルを異なる重みで平均してもよい」というところまできたわけです。であれば、その重みは入力空間内の点によっても異なっていいと思いませんか？いい換えると、ある場所ではモデル1が重く、ある場所ではモデル2が重いといったように、あたかも得意不得意で役割分担するイメージです。

その点で予測誤差が小さいモデルを重くするってこと？さすがにそれは後出しじゃんけんじゃない？というか、その点のノイズに引っ張られまくる気が。

いえ、ブートストラップ標本で学習したモデルでそれをやるということではないです。あるモデルはある場所から重点的にサンプリングした訓練データで学習し、また別のあるモデルは別の場所から重点的にサンプリングした訓練データで学習し…といったイメージです。それも入力空間を適当に区切るわけではなく、まだ上手く学習できていない箇所に重点を置きにいくんです。もはや個々のモデルの訓練データが異なるということです。…もうネタばらししてしまうんですが、10章のブースティング法がその手法です。その最も基本的なアルゴリズムである、アダブーストM1（10.1節）が以下です。ゴールは2クラス分類問題を解くことで、各分類器 $G_m(x)$ は $-1$ か $1$ を出力するという状況です。

各データの重み $\{w_i\}_{i=1}^N$ を均等に初期化する。
重み $\{w_i\}_{i=1}^N$ で分類器 $G_1(x)$ を学習する。
$G_1(x)$ の重み付き誤分類率 ${\rm err}_1$ を計算し、正解しやすさの対数オッズ $\alpha_1 = \log \bigl( (1 - {\rm err}_1)/{\rm err}_1 \bigr)$ を計算する。
各データの重みを更新する。 $G_1(x)$ が正しく予測できたデータの重みは更新しない。 $G_1(x)$ が正しく予測できなかったデータの重みには $e^{\alpha_1}$ をかける。
2. に戻る（更新した重み $\{w_i\}_{i=1}^N$ で分類器 $G_2(x)$ を学習する）。
最終的な予測モデルを $G(x) = {\rm sign} \bigl[ \sum_{m=1}^M \alpha_m G_m(x) \bigr]$ とする。

「正しく予測できなかったデータの重みを増幅しておく（ことで次以降のモデルに託す）」ことをやっているのがわかると思います。また、重みの増幅率やモデルを足し合わせる係数に対数オッズが出てくるのにも理由があります。

強引に10章にとんだな…。

ブースティングの話に触れておきたかったので。モデルのアンサンブルという文脈でバギングとブースティングが対比される場合が多いと思うんです。というよりは、ランダムフォレストと勾配ブースティング木が対比されるんでしょうか…しかし、テキスト10章の冒頭にもあるように両者は「本質的に異なる手法」なんです。どちらも決定木がたくさんあるくらいで。なので話を上手く10章にもっていけませんでした。なんていうか、一度「モデルを組み合わせよう」という気持ちを捨てた方がいい気がしますね。

うん、いきなりアダブーストM1っていわれてもブートストラップ標本が出てきたときより突拍子がないんだけど、ブートストラップ標本がベイズ推定から導出されるなら、そのアダブーストM1は何から導出されるの。

それが10.3節の「前向き段階的加法的モデリング」ですね。いま学習したいモデルが10.3式のように他のモデルの線形和でかけるとします。便宜上、足し合わせるモデルを弱学習器とよび、足し合わせたモデルを強学習器とよびます。10.3式のようなモデルは全てのパラメータを一気に最適化すべきですが、計算コストなどの問題でそれが上手くできないとき、弱学習器を1つずつ最適化できないかということになります。それが前向き段階的加法的モデリングに他なりません。391ページのアルゴリズム10.2です。

391ページのアルゴリズム10.2ね…って、387ページのアダブーストM1とだいぶ違わない？重みとか出てこないし。それに、アダブーストM1はステップ $m$ で学習した弱学習器の損失をみていたけど、この式だとステップ $m$ までの強学習器の損失って感じだし。

いえ、アルゴリズム10.2で $L$ を指数損失としてみましょう。そうする各ステップですべき最適化が10.9式になります。「ステップ $m$ までの強学習器の損失」が「重み」と「ステップ $m$ で学習した弱学習器の損失」の積になっていますよね。むしろ「重み付き誤分類率」とは「ステップ $m$ までの強学習器の損失」だったんです。だから重み付き誤分類率を最小化する弱学習器 $G_m(x)$ を学習すればいいんです。

なるほど。あれでも、弱学習器 $G_m(x)$ をどれだけの重みで強学習器に足せばいいんだ…って、10.12式か。え、これどうやって出すの？

演習10.1になっていますね…そうですね、以下で出ます。

$\sum_{i=1}^N w_i^{(m)} \exp \bigl( - \beta_m y_i G_m(x_i) \bigr)$ が最も小さくなればいいんですよね。
$\sum_{i \in {\rm OK}_m} w_i^{(m)} \exp \bigl( - \beta_m \bigr) + \sum_{i \in {\rm NG}_m} w_i^{(m)} \exp \bigl( \beta_m \bigr)$ と書き換えます。 ${\rm OK}_m$ は $G_m(x_i) = y_i$ であるインデックスの集合、 ${\rm NG}_m$ は $G_m(x_i) \neq y_i$ であるインデックスの集合とします。
$\beta_m$ についての微分がゼロなら $- \sum_{i \in {\rm OK}_m} w_i^{(m)} \exp \bigl( - \beta_m \bigr) + \sum_{i \in {\rm NG}_m} w_i^{(m)} \exp \bigl( \beta_m \bigr) = 0$ です。
よって $\exp \bigl( 2 \beta_m \bigr) \sum_{i \in {\rm NG}_m} w_i^{(m)} = \sum_{i \in {\rm OK}_m} w_i^{(m)}$ です。
よって $\displaystyle \beta_m =\frac{1}{2} \log \frac{ \sum_{i \in {\rm OK}_m} w_i^{(m)}}{\sum_{i \in {\rm NG}_m} w_i^{(m)}} =\frac{1}{2} \log \frac{ 1 - {\rm err}_m}{{\rm err}_m}$ です。

（その3があれば）つづく

2021-01-01

雑記：モデルをアンサンブルしたい話（その1―カステラ本7.3節、8.7節）

雑記

私の誤りは私に帰属します。お気付きの点がありましたらお手数ですがご指摘いただけますと幸いです。

テキスト（カステラ本）

統計的学習の基礎 ―データマイニング・推論・予測― | Trevor Hastie, Robert Tibshirani, Jerome Friedman, 杉山将, 井手剛, 神嶌敏弘, 栗田多喜夫, 前田英作, 井尻善久, 岩田具治, 金森敬文, 兼村厚範, 烏山昌幸, 河原吉伸, 木村昭悟, 小西嘉典, 酒井智弥, 鈴木大慈, 竹内一郎, 玉木徹, 出口大輔, 冨岡亮太, 波部斉, 前田新一, 持橋大地, 山田誠 |本 | 通販 | Amazon の 256～257, 326～327ページ。

関連記事

雑記：モデルを選択したい話（カステラ本7.4節～7.7節） - クッキーの日記

まとめ（解釈を含む；文字の定義は記事内を参照）

手元の訓練データでモデルを学習しある未知のデータ $x_0$ に対する2乗誤差を小さくしたいとする。手元の訓練データも $x_0$ 上の真の値も確率的なので、誤差 $f(x_0) + \varepsilon - \hat{f}(x_0)$ は確率変数であり、以下の3つの和で表せる。

$x_0$ 上の真の値がぶれる分（真の値のノイズ成分）： $\varepsilon$
訓練データのぶれによりモデル予測値が期待値に満たない分： $E\bigl[ \hat{f}(x_0)\bigr] - \hat{f}(x_0)$
モデル予測値が期待値であったとしても真の値に満たない分： $f(x_0) - E\bigl[ \hat{f}(x_0)\bigr]$ （これは確率的でない）

上の 1., 2., 3. の和の2乗を小さくしたい。が、確率的な成分があると議論しにくいので確率的な成分について期待値をとることにする。と、クロスタームは消え、1., 2., 3. の2乗の期待値の和だけが残る。このうち 1. の2乗はモデル側で小さくできないので、モデル側で小さくしうる項として 2. の2乗の期待値と 3. の2乗が残る。この前者をバリアンス、後者をバイアスの2乗とよぶ。
よって、期待2乗誤差を小さくするにはバリアンスとバイアスを小さくすればよいが、典型的なモデルで両者はトレードオフの関係にあり、一方を小さくすれば他方が大きくなるとわかる（具体的にはリッジ線形回帰など）。よって、手元の訓練データでモデルを学習する分にはこれらのバランスを取るように適当に正則化などするしかない。
ここで仮にもし、並行世界（この世界とは異なる訓練データが得られた世界）たちの自分から学習済みのモデルを取り寄せることができるなら、集めたモデルたちの出力の平均を取って新たなモデルとすることでバリアンスを抑えることができる（※ 複数のモデルの出力の平均を新たな出力にできる場合）。
しかし、並行世界たちの自分から学習済みのモデルを取り寄せることはできない。
そこで、手元で仮想的な並行世界たちをつくり、そこで学習したモデルたちを平均することが考えれる。特に、訓練データからブートストラップ標本たちを生成することによりそれを達成する手法はバギング（bagging: bootstrap aggregating）といわれる。

キャラクターの原作とは無関係です。

そういえば、カステラ本の7章でとばした箇所にあった、「バイアスと分散のトレードオフ」って何？

以下の問題を考えてみてください。どうなりますか？

ある世界では、気温 $X$ の日のアイスクリームの売り上げ $Y$ が $Y = f(X) + \varepsilon$ になるとします。

$f(\cdot)$ は決定的な関数で、 $\varepsilon$ は確率的な誤差で、 ${\rm E}(\varepsilon)=0, \; {\rm Var}(\varepsilon)=\sigma^2$ とします。

さて、この世界で、ある日の気温が $x_0$ でした。この日の売り上げを予測モデル $\hat{f}(\cdot)$ による予測値 $\hat{f}(x_0)$ で予測したときの期待2乗誤差はいくらでしょうか？なお、予測モデル $\hat{f}(\cdot)$ の確率的な成分は $\varepsilon$ と独立とします。

何その世界…ともかく、気温が $x_0$ の日の真の売り上げは $f(x_0) + \varepsilon$ だよな。それで、いま確率的なのは、 $\varepsilon$ と… $\hat{f}(x_0)$ もなのか。とりあえずこれらについての期待値を単に $E [ \cdot ]$ とかくと、期待2乗誤差は、

$\begin{split} E \Bigl[ \bigl( f(x_0) + \varepsilon - \hat{f}(x_0) \bigr)^2 \Bigr] &= E \Bigl[ f(x_0)^2 + \varepsilon^2 + \hat{f}(x_0)^2 + 2 f(x_0) \varepsilon - 2 f(x_0)\hat{f}(x_0) - 2 \hat{f}(x_0) \varepsilon \Bigr] \\ &= f(x_0)^2 + \sigma^2 + E \Bigl[ \hat{f}(x_0)^2 \Bigr] - 2 f(x_0) E \Bigl[ \hat{f}(x_0) \Bigr]\end{split}$

こうなるよな。 $f(x_0)$ は確率的じゃないし、独立な確率変数の積の期待値は期待値の積だし。

はい、間違っていませんが、それだと解釈しづらいですよね。「真の値の2乗とノイズの分散と予測値の2乗の期待値から真の値と予測値の期待値の積を引いたものです」といわれても。なのでこうしましょう。

$\begin{split} E \Bigl[ \bigl( f(x_0) + \varepsilon - \hat{f}(x_0) \bigr)^2 \Bigr] &= f(x_0)^2 + \sigma^2 + E \Bigl[ \hat{f}(x_0)^2 \Bigr] - 2 f(x_0) E \Bigl[ \hat{f}(x_0) \Bigr] \! - \! E \Bigl[ \hat{f}(x_0) \Bigr]^2 \! \! \! \! + \! E \Bigl[ \hat{f}(x_0) \Bigr]^2 \! \! \\ &= f(x_0)^2 + \sigma^2 + V \Bigl[ \hat{f}(x_0)^2 \Bigr] - 2 f(x_0) E \Bigl[ \hat{f}(x_0) \Bigr] \! + \! E \Bigl[ \hat{f}(x_0) \Bigr]^2 \\ &= \biggl\{f(x_0) - E \Bigl[ \hat{f}(x_0) \Bigr] \biggr\}^2 + V \Bigl[ \hat{f}(x_0)^2 \Bigr] + \sigma^2 \\ &= E \Bigl[ f(x_0) - \hat{f}(x_0) \Bigr]^2 + V \Bigl[ \hat{f}(x_0)^2 \Bigr] + \sigma^2 \end{split}$

こうすると「誤差の期待値（バイアス）の2乗と、予測値の分散（バリアンス）と、ノイズの分散の和」となりますよね。最初から予測値を期待値からのずれにしておけば一発ですけどね（以下）。

$\begin{split} E \biggl[ \Bigl( f(x_0) + \varepsilon - \hat{f}(x_0) + E \Bigl[ \hat{f}(x_0) \Bigr] - E \Bigl[ \hat{f}(x_0) \Bigr] \Bigr)^2 \biggr] &= \biggl\{f(x_0) - E \Bigl[ \hat{f}(x_0) \Bigr] \biggr\}^2 + V \Bigl[ \hat{f}(x_0)^2 \Bigr] + \sigma^2 \\ &= E \Bigl[ f(x_0) - \hat{f}(x_0) \Bigr]^2 + V \Bigl[ \hat{f}(x_0)^2 \Bigr] + \sigma^2 \end{split}$

何にせよ、2乗誤差を下図のように区分けして各マスの期待値をとっているだけです。

f:id:cookie-box:20201228135133p:plain:w500

俺に計算させた意味！あと図がごちゃごちゃしすぎ！！そもそもさ、期待2乗誤差が「誤差の期待値（バイアス）の2乗と、予測値の分散（バリアンス）と、ノイズの分散の和」だったら何なの？何かうれしいの？

「期待2乗誤差を小さくしたいなら、バイアスとバリアンスが小さいモデルにすべきである」といえるでしょう。ノイズはコントロールできませんから。

ああそういうことか。「ある点に対する誤差の期待値も小さいし、予測値自体もぶれないモデル」にすべきってことなんだな…って、いまいちどうすればいいかわからないんだけど？

実際にバイアスやバリアンスを小さくするにはどうすればいいのだろうと考えてみましょう。一般的な傾向として、トレードオフがありそうなことに気付くでしょう。

まず、バイアス＝誤差の期待値を小さくするためには、手元の訓練データ上での誤差を徹底的に小さくするべきです。モデルをいくら複雑にしてもです。だって、精度を上げる余地があるのに手加減してしまったら、その分の誤差を詰められませんから。
しかし、バリアンス＝予測値のぶれを小さくするには、手元の訓練データを徹底的に学ぶのは得策ではありません。なぜなら、訓練データはたまたま出たノイズを含みます。そのノイズまでしっかり学習してしまうようなモデルは、ノイズの出方によって予測値がぶれてしまいます。ぶれを抑えるには、あえて細かく学習させない工夫が要るでしょう。学習対象パラメータを制約してしまうのがその最たる例です。

実際、カステラ本の256～257ページに載っている、具体的なモデルでのトレードオフの例が以下の表の最初の3つです。 $k$ 近傍法では $k$ の大小によってトレードオフが発生し、最小2乗線形回帰ではリッジ正則化をかける大きさ $\lambda$ によってトレードオフが発生すると考えられます。 $k, \lambda$ を大きくするほどモデルが滑らかになり、小さくするほどモデルがでこぼこになるのが想像できると思います。また、以下の表の最後2つはウィキペディアにあった例です。

モデル $\hat{f}$	バイアス（誤差の期待値）	バリアンス（予測値の分散）
手元の訓練データから予測対象点 $x_0$ の最近傍 $k$ 点を選び、それらの点の実績値の平均値を予測値とするモデル。	$k$ を大きくするほど $x_0$ から離れた点が混ざってきてバイアスは大きくなる傾向にある。	$k$ を大きくするほど多くの点の実績値の平均を取るのでバリアンスは小さくなる傾向にある。
手元の訓練データで最小2乗線形回帰したモデル。つまり、 $\hat{f}(x_0) = x_0^\top (X^\top X)^{-1} X^\top Y$ とする。横ベクトル $h(x_0)=x_0^\top (X^\top X)^{-1} X^\top$ の各成分は、各データの実績値をどれだけの重みで取り込むべきかを意味する。	バイアスは「真のモデルと最良の線形近似との誤差の期待値」と「最良の線形近似といまの線形近似との誤差の期待値」に分解できる。後者は、何度も訓練データを取って学習したモデルの期待値をとれば、ゼロになる。	$\\|h(x_0)\\|^2 \sigma^2$ になる。
1つ上のモデルをリッジ正則化する。つまり、 $\hat{f}(x_0) = x_0^\top (X^\top X + \lambda I)^{-1} X^\top Y$ とする。	リッジ正則化したことにより「最良の線形近似といまの線形近似との誤差の期待値」はゼロにならなくなる。	$h(x_0)$ の逆行列の箇所に $\lambda I$ が加わった分、バリアンスは小さくなる。
ニューラルネットワーク。	例えば隠れ層のニューロン数を増やすとバイアスは小さくなる。	例えば隠れ層のニューロン数を増やすとバリアンスは大きくなる。
決定木。	例えば木を深くするとバイアスは小さくなる。	例えば木を深くするとバリアンスは大きくなる。

確かにその表の例だと、バイアスを下げるとバリアンスが上がって、バリアンスを下げるとバイアスが上がる傾向がありそうだな。これがトレードオフか…でも、それだと結局「期待2乗誤差が小さくなるように適宜ハイパーパラメータを調節しましょう」ってことにならない？いまいちバイアスとバリアンスに分解した甲斐がないっていうか…。

確かにそうですね。でも、例えば…ハヤトはここ1年の毎日の気温とアイスクリームの売り上げのデータをもとに、アイスクリーム売り上げ予測モデルを学習しました。そこにランプの精が現れていいました。「私は並行世界から来ました。並行世界のあなたが学習したモデルを差し上げます。並行世界の気温とアイスクリームの売り上げを生成する分布はこの世界と同じです。しかしこの世界と実現値はきっと異なるでしょう。予測に用いたモデルと学習方法はあなたと全く同じです」と。ちなみに同様のランプの精が計9人現れました。そしてハヤトは手元に自分が学習したモデル1つと、並行世界の自分が学習したモデル9つの、計10個のモデルを手に入れました。どうしますか？

ええ…まあ突っ込みはさておき、同じモデルならバイアスもバリアンスも同じだからどれがよいモデルとかないよな。まあモデルが10個あるならなんか平均してみたくなるけど。

ではモデルを平均しましょう。そうすると平均2乗誤差が小さくなることこそあれ、大きくなることはないとテキストの326～327ページにあります。訓練データを生成する分布を $\mathcal{P}$ とし、この世界のハヤトが学習したモデルを $\hat{f}^\ast(x)$ とし、それとあらゆる並行世界のハヤトたちが学習したモデルを平均したモデルを $f_{\rm ag}(x) = E_{\mathcal{P}} \bigl[\hat{f}^\ast(x)\bigr]$ とします。 $E_{\mathcal{P}} \bigl[\cdot\bigr]$ は色々な訓練データを得ることについての期待値です（と思っています）。すると、ある $(x,y)$ に対する2乗誤差の期待値について以下の不等式が成り立ちます（テキストでは $y$ が確率変数であるようにかかれていますが、この議論はどちらかというとある $y$ についてのものではないかと思っていますが、間違っていたらすみません）。

$\begin{split} E_{\mathcal{P}} \Bigl[ \bigl( y - \hat{f}^\ast(x) \bigr)^2 \Bigr] &= E_{\mathcal{P}} \Bigl[ \bigl( y- f_{\rm ag}(x) + f_{\rm ag}(x) -\hat{f}^\ast(x) \bigr)^2 \Bigr] \\ &= E_{\mathcal{P}} \Bigl[ \bigl( y - f_{\rm ag}(x)\bigr)^2 + \bigl( f_{\rm ag}(x) -\hat{f}^\ast(x) \bigr)^2 + 2\bigl( y - f_{\rm ag}(x)\bigr) \bigl( f_{\rm ag}(x) -\hat{f}^\ast(x) \bigr) \Bigr] \\ &= \bigl( y - f_{\rm ag}(x)\bigr)^2 + E_{\mathcal{P}} \Bigl[ \bigl( f_{\rm ag}(x) -\hat{f}^\ast(x) \bigr)^2 \Bigr] \\ &= \bigl( y - f_{\rm ag}(x)\bigr)^2 + V_{\mathcal{P}} \Bigl[ \hat{f}^\ast(x) \Bigr] \\ &\geqq \bigl( y - f_{\rm ag}(x)\bigr)^2 \end{split}$

つまり、1つのモデルの2乗誤差の期待値より、平均したモデルの2乗誤差の方が小さいか同じになります――モデルのバリアンスの分だけ。まあいまは $\mathcal{P}$ から生成されるあらゆる訓練データについて学習したモデルが手元にあるわけではなく、ある10セットの訓練データで学習したモデルが手元にあるだけですが、訓練データの出方の経験分布を $\mathcal{P}$ と考えれば話は同じはずです。

本当だ…あれでも、その論理だといつでも複数のモデルを平均した方がいいの？誤差を小さくしたかったら何でもいいから助っ人のモデルたちを用意すればいいってこと？？

ではありません。バイアスも平均されるわけですから、助っ人のモデルによってバリアンスが抑えられる以上にバイアスが増加したら意味がないです。何でもいいから寄せ集めればいいということにはなりません。

ああ確かに…いまは10個のモデルのバイアスの期待値が同じだから、10個のモデルを平均してもバイアスが増える心配はなかったのか。

それに、いまは回帰モデルで2乗誤差を損失とする場合でしたが、損失が異なる場合や、分類が目的の場合もありますよね。例えば個々のモデルが 0 か 1 を出力するような2値分類モデルであって、不正解率を損失とする場合、モデルをどうマージすればいいでしょうか。

えっ、うーん、個々のモデルが 0 か 1 を出しているなら、10個のモデルの出力を平均したらきっと 0.3 とか 0.6 とかになるよな。でも、正解か不正解をみたいなら最終的には 0 か 1 かを出さないといけないから…閾値を決めて、0.5 未満なら 0、0.5 以上なら 1 にするとか？ぴったり 0.5 はどう扱うべきか迷うけど…。

要は多数決ですね。しかしこの場合、マージすることが誤差を小さくすることにつながると限りません。テキスト327ページにある例ですが、あるデータの正解が 1 とします。そして、個々のモデルがこのデータに正しく 1 と出力できる確率が 0.4 とします。個々のモデルの正解率の期待値が 0.4 ということです。しかし、あらゆるモデルの多数決をとると必ず 0 を出力してしまいますね。4割のモデルが1、6割のモデルが0と判定するので。なので、多数決によって正解率がかえって 0 になってしまうのです。個々のモデルの正解率の期待値が 0.6 なら多数決によって正解率が 1 になるんですが。多数決を取る場合、多数派がよい予測をしていなければならないんです。こうかいてみると当然ですが。

なら、バイアスを小さくする方に振ってバリアンスはモデルの平均で抑えにいくのがいいってことなのか…って、いや、現実には並行世界からランプの精こないじゃん！

いかにも。なので、並行世界を自分でつくるしかありません。それがブートストラップ標本です。ブートストラップ標本とは、 $N$ 個のデータから $N$ 個のデータを復元抽出（抽出したサンプルを元に戻して次のサンプルを抽出していく）することを $B$ 回繰り返して $B$ セットの標本を得たものです（301ページ；正確にはノンパラメトリックブートストラップですが）。

え、うーん、そんなんでいいの？確かに標本を複数用意できるけど、なんか自作自演みたいな…。

（その2があれば）つづく