パターン認識と機械学習下（第6章：その2）

以下の本を読みます。上巻を読むこともあります。何か問題点がありましたらご指摘いただけますと幸いです。

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/02/29
メディア: 単行本
購入: 6人クリック: 14回
この商品を含むブログを見る

前回：その1 ／次回：まだ

f:id:cookie-box:20180305232608p:plain:w60

前回の 6.1 節では、「各訓練データを特徴空間に埋め込んで線形回帰する」という問題は、「入力空間内の各点に各訓練データが張る密度を線形回帰する」という問題に読み替えることができることを確認しましたね。この場合は $D$ 次元（ $D$ は特徴空間の次元数）の係数ベクトル $w$ を求めるのではなく $N$ 次元（ $N$ は訓練データの個数）の係数ベクトル $a$ を求めることになります。位置 $x$ に位置 $x'$ から張られる密度がカーネル関数 $k(x,x') = \phi(x)^{\top} \phi(x')$ でした（もっとも、カーネル関数は対称なので、位置 $x$ から位置 $x'$ に張る密度といっても構いませんが）。

f:id:cookie-box:20180305231302p:plain:w60

なあジュン、その「密度」って言い方引っかかるんだけど、特徴空間への写像 $\phi(\cdot)$ って別に内積を取ったら確率密度っぽくなるように選んでるわけじゃないだろ？適当に選んだ $\phi(\cdot)$ で $k(x,x_0) = \phi(x)^{\top} \phi(x_0)$ を入力空間全体で積分したら発散しちゃったりしない？ていうかだいたいいつも発散するんじゃない？

発散したらダメなんですか？

え？

僕は「確率」密度とはいってませんよ。確かに 2.5.1節「カーネル密度推定法」では目的が確率密度推定でした。でも今の目的は回帰や分類です。それぞれのデータ点が周囲に張り巡らす「場」は空間全体で積分したら発散するようなものであっても構いませんし、それを各点で足し上げる重みも負であっても構いません。2.5.1 節では推定する確率密度の構成要素として明示的に確率密度の条件を満たすカーネル関数 $k(x - x_n)$ を選びましたが、本節におけるカーネル関数 $k(x, x')$ はハヤトの言う通りこんなカーネル関数がいいと選んだものではなく「特徴の内積」として結果的に出てきたものです。といっても、実際にカーネル法で解こうとするような場合はやはり特徴ではなくカーネル関数の方を決めるようですね。それを 6.2 節でみていきましょう。

こんがらがってきたな…いま特徴を決めて線形回帰しようとしてたら、「特徴と各訓練データの特徴との内積（カーネル関数）」を線形回帰してもいいじゃんって言われたのが 6.1 節で、さらに特徴じゃなくてカーネル関数を決めろって言われてる状況？どんだけカーネル関数ごり押しだよ…まあ先に進むか。6.2 節には、「カーネル関数を構成するには、特徴から構成するアプローチと、カーネル関数を直接定義するアプローチとがある」って書いてあるな。え、だから特徴の内積がほしいカーネル関数になるように狙って特徴つくるの難しくない？基底関数って？あと5ページの上の図 6.1 何これ？

ちょっと 6.2 節の冒頭趣旨がわかりづらいですね…先に図 6.1 ですが、要するにこういうことですね（※ スクリプトは記事の最下部です）。パラメータは目算で合わせました。

f:id:cookie-box:20181114200048p:plain:w660

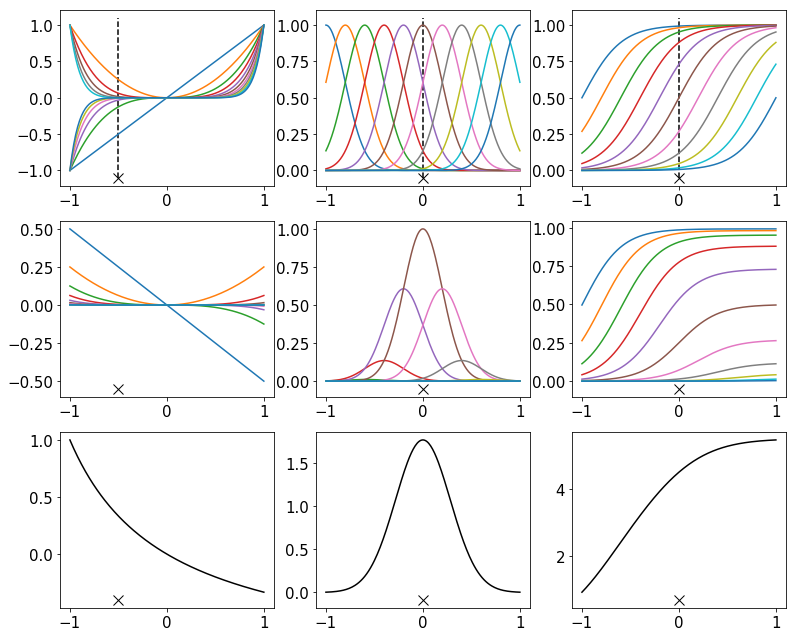
あ、図 6.1 と同じ絵…だけど、何も要するにになってないし。あと、図 6.1 では上段と下段しかないけどその中段は何？まあ上段と下段も何なのかわかんないけど。

真ん中の列が一番わかりやすいんじゃないかと思うんです。手書き数字のグレースケール画像を分類するような場合を想像してください。もっともその場合は入力空間は1次元でなく画像のピクセル数の次元があるわけですが、上のグラフは1次元ですし無理やり1次元だと考えてください。同じ正解ラベルをもつ画像は入力空間での距離が近いと考えるのが自然でしょう。未知データに対する予測も、その未知データに近い訓練データがより大きな影響を及ぼすようなものであってほしいです。なので、個々の訓練データは入力空間に、そのデータの位置で最も濃く、データから離れるほど薄くなるようなカーネル関数の煙幕を張りたいんです。中央列の最下段のように。

あー、この図の最下段は「 $x$ 軸上の各点とバツ印の点（にある訓練データ）とのカーネル関数」なのか。

しかし問題はこのようなカーネル関数を得るのにどのような特徴をとればいいのかということですが…天下りになってしまいますが、このようなカーネル関数を得るには「入力空間で少しずつ中心をずらしたガウス関数たちを特徴とすればよい」んです。中央列の最上段のカラフルな関数たちが特徴 $\phi(x)$ の各成分 $\phi_i(x)$ です。そして中段は $\phi_i(x) \phi_i(x')$ を各 $i$ についてプロットしたものです。中段を全て足し合わせたのが最下段 $k(x,x') = \phi(x)^{\top} \phi(x')$ です。最上段のプロットには訓練データの位置に破線を入れていますが、最上段の例えばピンク色の曲線を、「破線との交点の値」倍すると中段のピンク色の曲線に移ります。もちろん他の色の曲線（特徴）もそうです。そして、スクリプトをコピーして x_dash の値を変えてみてもらえると確かにわかると思いますが、バツ印の位置を横にずらせば中央列最下段の分布も横にずれます。色々な位置の訓練データ点に対してこのように訓練データを中心にした密度を張り巡らせることができるので理想的なわけです。

えー Jupyter Notebook 起動すんのめんどい。バツ印をずらした場合もわかるようにアニメーションとかにしといてよ。

忙しいから無理。

じゃあ左の列と右の列は何なの？これらは訓練データを中心に広がる分布、って感じじゃないけど…。

右の列は2値分類のようなイメージですね。迷惑メールかどうかの分類で、「このメールよりあちら側なら迷惑メールっぽいし、こちら側なら迷惑メールっぽくない」という煙幕でしょうか。この最上段の各特徴は中心を少しずつずらしたシグモイド関数です。左の列は解釈が難しいので説明を割愛します。

ぶん投げた！

ただ、左の列の最上段の各特徴は $\phi_i(x) = x^i$ です。あ、それに関連して、基底関数というのは「あるクラスに含まれる関数たちの全てがその関数の線形結合であらわせる」ようにとった関数たちのことです。例えば $f(x)=a_0 + a_1 x + a_2 x^2 + \cdots$ の形でかけるような関数全体（多項式関数というクラス）の基底関数は $\phi_i(x) = x^i \; (i=0, 1, 2, \cdots)$ ととることができます。そのままですね。なので、多項式関数状のカーネル関数の煙幕を張りたいならばその基底関数である $\phi_i(x) = x^i$ を特徴たちとして採用する、ということもあり得るのかもしれませんが…ただ、特徴たちをカーネル関数に統合するときに否応なく個々の訓練データ点での $\phi_i(x')$ が線形結合の重みとなりますから、煙幕の形をそう自由にデザインできるわけでもないと思うんですよね。「こんな形状のカーネル関数にしたいから、その基底関数を特徴にしよう」という流れは僕にはどうにも想像しにくいんです。なので、ここで「基底関数」というのもどうなのかなと。しかし、僕が不勉強なだけかもしれません。あるいは、ことさら関数解析を意識しているわけではなく、この節の用語としての基底関数（basis function）の可能性もありますけど。…6.2 節の1段落目はこれくらいにしておいて、カーネル関数を直接定義するアプローチの方に移りましょう。

2段落目からはそのアプローチだな。カーネル関数を直接決めていいならそりゃ好きな形にできそうだけど、でも全く好きにカーネル関数を選ぶわけにはいかないよな。特徴の内積の形でかけなきゃだから。で、 $k(x,x')$ がそういう形になっているかは (6.12) 式みたいに個々にまともに調べる方法もあるけど、それじゃ大変だよな。そこで $k(x,x')$ が有効なカーネルであるための必要十分条件があるのか。それは、成分が $k(x_n, x_m)$ で与えられるグラム行列 $K$ が半正定値であること…半正定値って何？

実対称行列の固有値が全て非負である場合、半正定値行列であるといいますね。他の同値な条件で表現されることもありますが。

半正定値行列の同値な４つの定義（性質）と証明 | 高校数学の美しい物語

本には証明がありませんが、グラム行列 $K$ （サイズ $N \times N$ ）が半正定値行列ならば $k(x,x')$ が有効なカーネルであることを軽く確認しておきましょうか。

$K$ は実対称行列なので、適当な直交行列 $P$ によって $P^{\top} KP = \Lambda$ を $K$ の各固有値（重複含む）を対角成分とする対角行列とすることができます。証明をかくのは面倒なので以下を参照してください。

線形代数Ｉ/実対称行列の対角化 - 武内＠筑波大

$K$ の固有値は全て非負なのでルートをとることができます。 $\Lambda$ の対角成分に全てルートをかぶせた行列を $\hat{\Lambda}$ とします。 $P^{\top} KP = \Lambda = \hat{\Lambda} \hat{\Lambda}$ とかけます。さらに $K = P \hat{\Lambda} \hat{\Lambda} P^{\top} = P \hat{\Lambda} ( P \hat{\Lambda} )^{\top} \equiv \Phi \Phi^{\top}$ とできます。 $\Phi$ の各行をとれば $k(x_n, x_m) = \phi(x_n)^{\top} \phi(x_m)$ とかけます。これだけ満たされれば 6.1 節の議論は問題なく成り立ちますね。つまり、 $k(x,x')$ は有効なカーネル関数であるといえるでしょう。

ふーん…でも、 $K$ が半正定値行列かどうかの確認もそれはそれで大変なんじゃない？ $K$ って縦幅も横幅もデータサイズなんだろ？

正定値性判定のアルゴリズムは色々あるんじゃないですか。詳しくないですが。まあでも、本にも、新しいカーネルをつくるには既知のカーネルから (6.13)～(6.22) の式変形を用いてつくるのが便利みたいにかいてありますね。というかこれらの式の証明全部演習問題なんですね…。

この6ページの画像のピクセルがどうって何？

(6.12) 式の例だと $\phi(x) = (x_1^2, \sqrt{2} x_1 x_2, x_2^2)^{\top}$ のように特徴に入力変数の2次の組み合わせが全てあらわれていますよね。それと同様に、特徴にあらゆる $M$ 次の組み合わせがあらわれるということですね。まあそれを画像のピクセルに喩えられても、 $M$ 個のピクセルを掛け合わせるときに個々に重みを設定するわけでもないので畳み込みともちょっと違う気がしますが。しいていうなら、未知画像のあらゆる $M$ 個のピクセルを掛け合わせた特徴たちを、訓練データたちが与える重みで畳み込むという感じはするかもしれませんが。

カーネル法は画像認識にもつかえるって言いたいのかな？わかんないけど。その次のガウスカーネルはジュンが前回やっちゃったな。

7ページには、ガウスカーネルの2乗ノルムの部分を好きな非線形カーネルに置き換えてもよいとありますね。

（次回があれば）つづく

※ スクリプト

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 13,11
rcParams['font.size'] = 15

# カーネル関数 k(x, x') = Σ_{i=1}^M phi_i(x)*phi_i(x')
def kernel(phi, x, x_dash, M):
    k_ = 0
    for i in range(1, M + 1):
        k_ = k_ + phi(i, x) * phi(i, x_dash)
    return k_

# プロット用
def my_plot(phi, x, x_dash, M, axes):
    # (上段) 基底関数をそれぞれプロット
    for i in range(1, M + 1):
        axes[0].plot(x, phi(i, x))
    xmin, xmax, ymin, ymax = axes[0].axis()
    axes[0].plot(x_dash, ymin, 'kx', markersize=10)
    axes[0].vlines([x_dash], ymin, ymax, 'black', linestyles='dashed')
    # (中段) 足し合わせる前のカーネル関数をプロット
    for i in range(1, M + 1):
        axes[1].plot(x, phi(i, x) * phi(i, x_dash))
    axes[1].plot(x_dash, axes[1].axis()[2], 'kx', markersize=10)
    # (下段) カーネル関数をプロット
    axes[2].plot(x, kernel(phi, x, x_dash, M), 'k-')
    axes[2].plot(x_dash, axes[2].axis()[2], 'kx', markersize=10)

# =========================
# 色々な基底関数を定義
# =========================
# 多項式型の基底関数 phi_i(x) = x^i
def phi_poly(i, x):
    phi_ = 1
    for i_ in range(i):
        phi_ = phi_ * x
    return phi_

# ガウス型の基底関数 phi_i(x) = exp(-0.5 * (x-mu)^2 / s^2)
mu = np.arange(-1.2, 1.01, 0.2) # 平均の位置は -1.2(0番目は無視), -1.0, -0.8, ..., 1.0
s = 0.2 # 標準偏差
def phi_gaussian(i, x):
    return np.exp(-0.5 * (x - mu[i]) * (x - mu[i]) / (s * s))

# シグモイド型の基底関数 phi_i(x) = 1 / (1 + exp(-(x-mu)))
a = 5.0 # シグモイド関数のゲイン
def phi_sigmoid(i, x):
    return 1.0 / (1.0 + np.exp(-a * (x - mu[i])))

# =========================
# プロット
# =========================
fig = plt.figure()
M = 11 # 基底関数をいくつとるか＝特徴の次元数
x = np.arange(-1.0, 1.01, 0.01) # プロットする x の範囲
x_dash = -0.5 # ある訓練データ点
my_plot(phi_poly, x, x_dash, M, [fig.add_subplot(3, 3, 1), fig.add_subplot(3, 3, 4), fig.add_subplot(3, 3, 7)])
x_dash = 0.0 # ある訓練データ点
my_plot(phi_gaussian, x, x_dash, M, [fig.add_subplot(3, 3, 2), fig.add_subplot(3, 3, 5), fig.add_subplot(3, 3, 8)])
my_plot(phi_sigmoid, x, x_dash, M, [fig.add_subplot(3, 3, 3), fig.add_subplot(3, 3, 6), fig.add_subplot(3, 3, 9)])
plt.show()