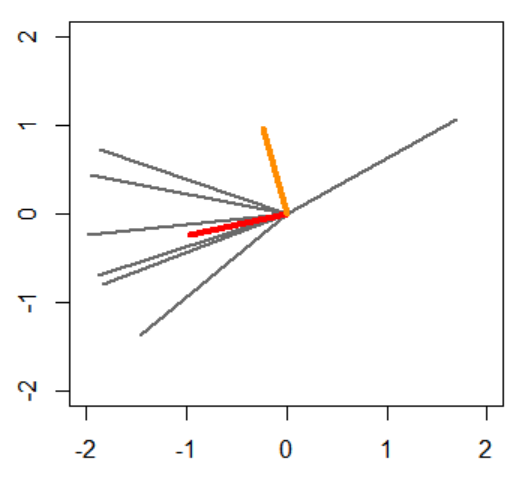
以下の赤い本の9章を読みます。キャラクターは適当です。誤りがありましたらご指摘いただけますと幸いです。 「変化を検知したい」ってときありますよね。この本の9章を読みたいです。 導入が雑…。 最初の累積和法は、「正常状態の分布」「異常状態の分布」を所与として、逐次的に観測される変数が異常状態の方に近い場合にだけ異常さのポイントを積み上げる手法のようですね。…「正常状態の分布」「異常状態の分布」がわかってたら苦労しなくないですか? いやまあそこがわかってたらかなりありがたいけど、じゃあどちらの分布に近いのかというのを対数尤度比という形で定量化して、さらにそれを時系列データにおける継続的な異常状態の検知に適用するために累積和という指標にまとめる、というのも大事な仕事なんじゃないかな。 そう、その「継続的な異常状態の検知」という点についてもなんですが、この累積和って異常の継続性を考慮してますか? 「たまに異常になる分には目をつぶって、継続的に異常になったら検知したい」ということで累積和をとったということですが、これって異常が連続していようと数回おきであろうと足し上げていくだけですよね。異常が継続していなくても累積和はどんどん降り積もっていきません? そういう場合は定期的にリセットするんでしょ。結局ある一定の期間内の異常さの和に閾値を置いているのと等しいとは思うよ。ある一定の期間内に多くの異常が発生することがここでの継続的な異常なんだと思う。 なるほど。…次に紹介されているのは近傍法ですね。この手法で少なくとも所与とするのは「正常な部分時系列のセット」ですね。それで、検査対象の部分時系列を入力すると、最も近い正常な部分時系列までの距離(の対数の定数倍)を返すといった具合ですね。 k=1 の k 近傍法で、明示的に異常標本を与えずにとにかく異常度のみ算出する場合はその手続きになるね。 いや、カルバック・ライブラー情報量ですね。 はい。 KL情報量は非対称だけど、これは「参照データの分布が厚いところで検査データの分布が薄いことを問題視する」って向きだね。参照データにはよく見られるようなデータが検査データに全然見られなかったらおかしいだろうと。狭い参照データ分布をカバーするように広い検査データ分布よりは、広い参照データ分布をカバーし切らない狭い検査データ分布の方が相違度が大きくなるね。例えば、 参照データ分布としてそんなにだらだら広がった分布を仮定しない方がよさそうですね。検査データ分布側の密度の欠落に厳しくなりそうです。 116ページからは、(9.8) 式の具体的な計算手法が1つ紹介されていて、つまり、特異スペクトル変換法だね。 フォンミーゼス・フィッシャー分布…扱ったことがないですね…7章を参照するとこれは、M次元超球面上に定義される分布ということですが…なぜこんな分布を導入するのでしょう…。 参照データ分布と検査データ分布にフォンミーゼス・フィッシャー分布(長いので以下vMF分布)を仮定するということだけど、(少なくともこの本の)特異スペクトル法の手順の中で「集中度」は推定せず参照データ分布も検査データ分布も適当な同一の集中度を取ると仮定しているから、結局推定対象パラメータは「平均方向」のみで、だから「参照データセットと検査データセットをそれぞれ表現するvMF分布って何だろう」というよりは、実質的には「参照データセットと検査データセットをそれぞれ代表する単位ベクトルって何だろう」ってことだね。そういう単位ベクトルを求めたらそれらを平均方向とするvMF分布どうしのKL情報量を相違度とするわけだけど。ともあれ単位ベクトルの求め方が肝心そうだね。いや…単位ベクトル自体を求めるわけじゃなくて、そのような単位ベクトルどうしの内積に相当する値を直接求めにいってるね。 参照データの第i成分を全て束ねたM本のベクトルをどのようなM個の係数の組み合わせで線形結合するとそのL2ノルムが極値になるかを考える(ただし、M個の係数の2乗和は1という制約の下で)。極値を与える係数のセット(=左特異ベクトル)がMセット求まる。最も大きい極値を与える左特異ベクトルは参照データを特徴付けるベクトルだろう、って感じだね。だから参照データのそれと検査データのそれの内積を取れば相違度がわかるだろうと。ただ最も大きい極値以外無視するというのもあれだっていうなら特異値上位の何本かずつ左特異ベクトルを選ぶわけだけど、例えば2本ずつ選んだら内積が4パターン計算できちゃう。どうやってトータルの相違度とすべきかわからない。そのときは、ここでまたしても各行ベクトル(列ベクトルでもいいけど)の各成分をどのように線形結合するとL2ノルムが極値になるかという問題を解いて、最大の極値(最大特異値)をトータルの相違度とするんだね。この操作は それが118ページでいう「一番人気のある方向」だね。 ちょっと図示してみたいですね。ランダムな2次元データセットを生成して、左特異ベクトルをプロットしてみましょう。こんな感じでいいんでしょうか。灰色のベクトルたちを代表するのが赤いベクトルになると期待しているんですが…。 だから、特異スペクトル変換の定義を modify するみたいだね。もう検査データ側の特異値分解はしないことにして、代表的なデータを選んで(全て選んで後で相違度を何らかの方法で集約してもいいけど)左特異ベクトルの変わりにするみたいだね。 いや部長は高校1年生だよね!? 幼稚園の年長に数値計算の授業はないよね!?
異常検知と変化検知 (機械学習プロフェッショナルシリーズ)
井手 剛 杉山 将
講談社 2015-08-08
売り上げランキング : 56236
Amazonで詳しく見る by G-Tools











(参照データ分布の方が狭い場合)
(参照データ分布の方が広い場合)






の行列2ノルムを取ることと等しい。



n <- 7
x <- c()
for (i in 1:n) {
t <- runif(1, min=0, max=2)
x <- c(x, 2*cos(pi*t), 2*sin(pi*t))
}
x <- matrix(x, nrow=2)
plot(c(-2,2), c(-2,2), xlab="", ylab="", type="n")
for (i in 1:n) {
lines(c(0, x[[1,i]]), c(0, x[[2,i]]), lwd=2, col="dimgray")
}
res <- svd(x)
lines(c(0, res$u[[1,1]]), c(0, res$u[[2,1]]), lwd=4, col="red")
lines(c(0, res$u[[1,2]]), c(0, res$u[[2,2]]), lwd=4, col="darkorange")
print(res)



異常検知と変化検知: 9章メモ(部分空間法による変化検知)
他の章のメモ:まだ