機械学習をしているとよく交差エントロピーを最小化させられると思います。
でも冷静に考えると交差エントロピーが何かよくわかりませんでした。むしろエントロピーがわかりませんでした。
以下の記事を読み、もっと無理がない例で短くまとめたかったのですが、やはり例に無理があり、長くなってしまいました。
A国、B国、C国があります。
A国では、一日の天気は25%ずつの確率で晴れ、曇り、雨、雪になります。B国では、晴れになる確率が50%、曇りになる確率が25%、雨か雪になる確率が12.5%ずつです。C国では天気は晴れにしかなりません。この3国の天気の確率関数をグラフに表すと以下のようになります。
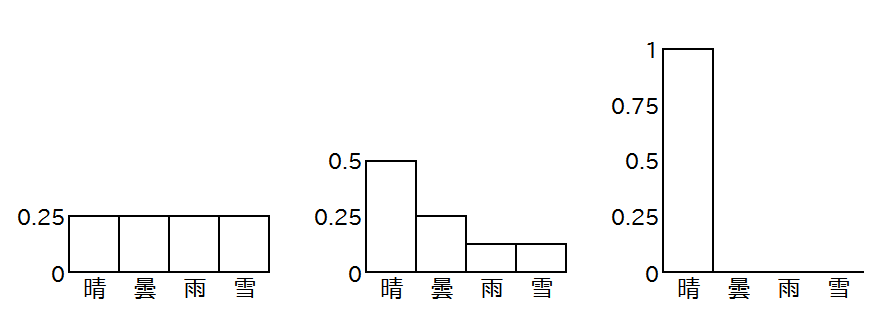
または、それぞれの天気になる確率を横向きの積み上げ棒グラフで表すと以下のようになります。
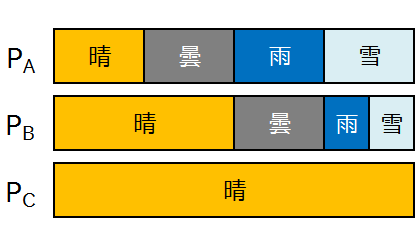
あるとき、A国の気象庁に勤めるアリスは、A国内の大学から「過去の天気のデータをなるべくたくさんの日数ほしい」と申請を受けました。A国の法律で、気象庁からの情報提供は1枚のフロッピーディスク(死語)によって行うことになっていましたが、この架空の世界では記録媒体技術が残念だったのでフロッピーディスクの容量が1KB(8000ビット)しかありませんでした。しかも経費削減のため1件の情報提供にディスクは1枚しかつかえませんでした。そこで、アリスは容量を最大限に活用するためそれぞれの天気を「晴:00、曇:01、雨:10、雪:11」にエンコードし、1日の天気の情報を2ビットで表現することで、4000日分のデータを提供しました(8000 ÷ 2 = 4000)。
同じころ、B国の気象庁に勤めるボブもB国内の大学から同じ申請を受けました。B国も情報提供に係る制約はA国と同じです。ボブは、最初はアリスのように「晴:00、曇:01、雨:10、雪:11」というエンコードで情報を提供しようとしましたが、B国ではそれぞれの天気の確率に偏りがあることに気付きました。ボブは「晴:0、曇:10、雨:110、雪:111」と、確率が大きい晴れに短いビット数を割り振り、その代わり確率が小さい雨と雪に長いビット数を割り振ることで、1日の天気の情報の平均ビット数を 0.5*1 + 0.25*2 + 0.125*3 + 0.125*3 = 1.75 ビットにしました。こうすることで、8000ビットのディスクで4500日以上分のデータを提供しました(8000 ÷ 1.75 > 4500)。
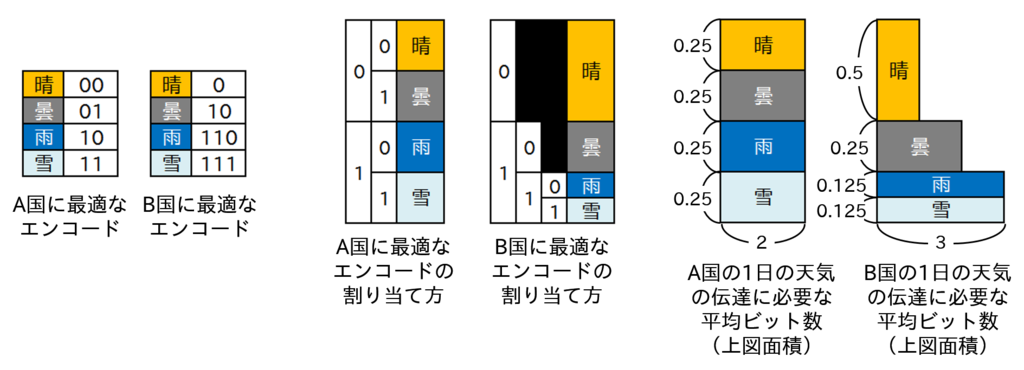
アリスよりボブが同じ容量のディスクでよりたくさんの日数の情報を提供できたのは、ボブの方が優れたエンコードをしたからではありません。何ならクリスはディスクをつかうまでもなく無限の日数の情報を提供できています。1回の試行の結果(ある1日の天気)を伝えるのに必要な平均ビット数の最小値は確率分布によってのみ決まります。つまり、確率 で起きるできごとに長さ
で起きるできごとに長さ  のコードを割り当てるのが最適になります(証明略)。この最適なエンコードのとき、「晴、曇、雨、雪」を伝えるのに要するそれぞれのビット数
のコードを割り当てるのが最適になります(証明略)。この最適なエンコードのとき、「晴、曇、雨、雪」を伝えるのに要するそれぞれのビット数  を情報量(選択情報量)、その期待値(1回の試行の結果を伝えるのに要する平均ビット数)をエントロピー(平均情報量)とよびます(以下)。
を情報量(選択情報量)、その期待値(1回の試行の結果を伝えるのに要する平均ビット数)をエントロピー(平均情報量)とよびます(以下)。
![\displaystyle H(P) = E_P \left[ \log \frac{1}{P(\omega)} \right] = \sum_{\omega \in \Omega} P(\omega) \log \frac{1}{P(\omega)}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cdisplaystyle%20H%28P%29%20%3D%20E_P%20%5Cleft%5B%20%5Clog%20%5Cfrac%7B1%7D%7BP%28%5Comega%29%7D%20%5Cright%5D%20%3D%20%5Csum_%7B%5Comega%20%5Cin%20%5COmega%7D%20P%28%5Comega%29%20%5Clog%20%5Cfrac%7B1%7D%7BP%28%5Comega%29%7D)
A国、B国、C国それぞれの、「1日の天気を調べる」という試行のエントロピーは以下です。
![\begin{cases} H(P_A)=E_{P_A}\left[ \log_2(1/P_A(\omega)) \right]=0.25 \log_2 (1/0.25)+0.25 \log_2 (1/0.25)+0.25 \log_2 (1/0.25)+0.25 \log_2 (1/0.25)=2 \\ H(P_B)=E_{P_B}\left[ \log_2(1/P_B(\omega)) \right]=0.5 \log_2 (1/0.5)+0.25 \log_2 (1/0.25)+0.125 \log_2 (1/0.125)+0.125 \log_2 (1/0.125)=1.75 \\ H(P_C)=E_{P_C}\left[ \log_2(1/P_C(\omega)) \right]=1 \log_2 (1/1) =0\end{cases}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cbegin%7Bcases%7D%20H%28P_A%29%3DE_%7BP_A%7D%5Cleft%5B%20%5Clog_2%281%2FP_A%28%5Comega%29%29%20%5Cright%5D%3D0.25%20%5Clog_2%20%281%2F0.25%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%3D2%20%5C%5C%20H%28P_B%29%3DE_%7BP_B%7D%5Cleft%5B%20%5Clog_2%281%2FP_B%28%5Comega%29%29%20%5Cright%5D%3D0.5%20%5Clog_2%20%281%2F0.5%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%2B0.125%20%5Clog_2%20%281%2F0.125%29%2B0.125%20%5Clog_2%20%281%2F0.125%29%3D1.75%20%20%5C%5C%20H%28P_C%29%3DE_%7BP_C%7D%5Cleft%5B%20%5Clog_2%281%2FP_C%28%5Comega%29%29%20%5Cright%5D%3D1%20%5Clog_2%20%281%2F1%29%20%3D0%5Cend%7Bcases%7D)
情報量を「その試行の結果を知らされたときの価値」、エントロピーを「1回の試行の結果の結果を知らされたときの価値の期待値」と解釈する人もあります。あるできごとを知らされたときの価値は、そのできごとが珍しいほど高くなります。A国ではどの天気になる確率も等しいので、どの天気だと知らされても等しく2の価値があります。B国では晴れになる確率が高いので、晴れだと知らされたときの価値は1しかありませんが、雨や雪になる確率は低いので、雨や雪だと知らされたときの価値は3あります。また、C国で晴れだと知らされても価値は0です。この価値の平均としてのエントロピーは不確実さが大きいほど(確率分布がばらつくほど)大きくなります。天気の不確実さは A国 > B国 > C国 の順になっているといえるでしょう。
ところであるとき、B国の大学でA国の天気のデータが必要になりました。B国の大学の人はボブ式のエンコードに慣れていたので、A国のアリスに、B国のボブ式のエンコードでA国の天気のデータを送るよう依頼しました。アリスは言われた通りにしましたが、A国の天気をボブ式にエンコードすると、1日あたりの平均ビット長が 1*0.25 + 2*0.25 + 3*0.25 + 3*0.25 = 2.25 になってしまうことに気付きました。この世界の残念なフロッピーディスクでは3600日分のデータも提供することができませんでした(8000 ÷ 2.25 < 3600)。
同じころボブもA国の大学の人にアリス式のエンコードでB国の天気データを提供するよう要請されました。アリス式のエンコードはどの天気にも2ビットをあてがうので、B国の天気をエンコードしても平均ビット長が2ビットになりました。ボブは、「自分のエンコードなら、この国の天気を1日あたり1.75ビットに圧縮できるのになあ」と思いました。
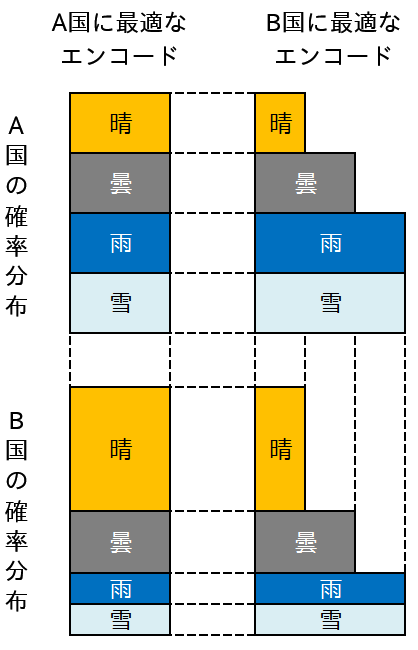
ある確率分布に最適化された方式で別の確率分布をエンコードしたときの平均ビット長を交差エントロピーとよびます。
![\displaystyle H(P, Q) = E_P \left[ \log \frac{1}{Q(\omega)} \right] = \sum_{\omega \in \Omega} P(\omega) \log \frac{1}{Q(\omega)}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cdisplaystyle%20H%28P%2C%20Q%29%20%3D%20E_P%20%5Cleft%5B%20%5Clog%20%5Cfrac%7B1%7D%7BQ%28%5Comega%29%7D%20%5Cright%5D%20%3D%20%5Csum_%7B%5Comega%20%5Cin%20%5COmega%7D%20P%28%5Comega%29%20%5Clog%20%5Cfrac%7B1%7D%7BQ%28%5Comega%29%7D)
![\begin{cases} H(P_A, P_B)=E_{P_A}\left[ \log_2(1/P_B(\omega)) \right]=0.25 \log_2 (1/0.5)+0.25 \log_2 (1/0.25)+0.25 \log_2 (1/0.125)+0.25 \log_2 (1/0.125)=2.25 \\ H(P_B, P_A)=E_{P_B}\left[ \log_2(1/P_A(\omega)) \right]=0.5 \log_2 (1/0.25)+0.25 \log_2 (1/0.25)+0.125 \log_2 (1/0.25)+0.125 \log_2 (1/0.25)=2 \end{cases}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cbegin%7Bcases%7D%20H%28P_A%2C%20P_B%29%3DE_%7BP_A%7D%5Cleft%5B%20%5Clog_2%281%2FP_B%28%5Comega%29%29%20%5Cright%5D%3D0.25%20%5Clog_2%20%281%2F0.5%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%2B0.25%20%5Clog_2%20%281%2F0.125%29%2B0.25%20%5Clog_2%20%281%2F0.125%29%3D2.25%20%5C%5C%20H%28P_B%2C%20P_A%29%3DE_%7BP_B%7D%5Cleft%5B%20%5Clog_2%281%2FP_A%28%5Comega%29%29%20%5Cright%5D%3D0.5%20%5Clog_2%20%281%2F0.25%29%2B0.25%20%5Clog_2%20%281%2F0.25%29%2B0.125%20%5Clog_2%20%281%2F0.25%29%2B0.125%20%5Clog_2%20%281%2F0.25%29%3D2%20%5Cend%7Bcases%7D)
これはエンコードを誤ったようなイメージです。エンコードを誤ると、めずらしいできごとに小さなビット長を割り振ってしまう影響よりも、めずらしくないできごとに大きなビット長を割り振ってしまう影響の方が必ず大きくなり、必要な平均ビット長が大きくなってしまいます( )。つまり、ビット長の無駄が生じます。
)。つまり、ビット長の無駄が生じます。
 は「B国の情報の価値尺度でA国の情報を受け取ったときの平均的な価値」と解釈することもできます。B国ではめずらしい雨や雪が、A国では比較的めずらしくないので、その分A国の天気をA国の尺度で受け取るよりも、A国の天気をB国の尺度で受け取った方が価値が上がってしまいます。
は「B国の情報の価値尺度でA国の情報を受け取ったときの平均的な価値」と解釈することもできます。B国ではめずらしい雨や雪が、A国では比較的めずらしくないので、その分A国の天気をA国の尺度で受け取るよりも、A国の天気をB国の尺度で受け取った方が価値が上がってしまいます。
このビット長の無駄/価値の誤差 をカルバック・ライブラー情報量とよびます。
をカルバック・ライブラー情報量とよびます。
![\displaystyle D_{\rm KL}(P \, || \, Q) =H(P,Q)-H(P)= E_P \left[ \log \frac{1}{Q(\omega)} - \log \frac{1}{P(\omega)} \right] = E_P \left[\log \frac{P(\omega)}{Q(\omega)} \right] = \sum_{\omega \in \Omega} P(\omega) \log \frac{P(\omega)}{Q(\omega)}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cdisplaystyle%20D_%7B%5Crm%20KL%7D%28P%20%5C%2C%20%7C%7C%20%5C%2C%20Q%29%20%3DH%28P%2CQ%29-H%28P%29%3D%20E_P%20%5Cleft%5B%20%5Clog%20%5Cfrac%7B1%7D%7BQ%28%5Comega%29%7D%20-%20%5Clog%20%5Cfrac%7B1%7D%7BP%28%5Comega%29%7D%20%5Cright%5D%20%3D%20E_P%20%5Cleft%5B%5Clog%20%5Cfrac%7BP%28%5Comega%29%7D%7BQ%28%5Comega%29%7D%20%5Cright%5D%20%3D%20%5Csum_%7B%5Comega%20%5Cin%20%5COmega%7D%20P%28%5Comega%29%20%5Clog%20%5Cfrac%7BP%28%5Comega%29%7D%7BQ%28%5Comega%29%7D)
![\begin{cases} D_{\rm KL}(P_A \, || \, P_B)=E_{P_A}\left[ \log_2(1/P_B(\omega)) - \log_2(1/P_A(\omega)) \right]=0.25 (1-2)+0.25 (2-2)+0.25 (3-2)+0.25 (3-2)=0.25 \\ D_{\rm KL}(P_B \, || \, P_A)=E_{P_B}\left[ \log_2(1/P_A(\omega)) - \log_2(1/P_B(\omega)) \right]=0.5 (2-1)+0.25 (2-2)+0.125 (2-3)+0.125 (2-3)=0.25 \end{cases}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cbegin%7Bcases%7D%20D_%7B%5Crm%20KL%7D%28P_A%20%5C%2C%20%7C%7C%20%5C%2C%20P_B%29%3DE_%7BP_A%7D%5Cleft%5B%20%5Clog_2%281%2FP_B%28%5Comega%29%29%20-%20%5Clog_2%281%2FP_A%28%5Comega%29%29%20%5Cright%5D%3D0.25%20%281-2%29%2B0.25%20%282-2%29%2B0.25%20%283-2%29%2B0.25%20%283-2%29%3D0.25%20%5C%5C%20D_%7B%5Crm%20KL%7D%28P_B%20%5C%2C%20%7C%7C%20%5C%2C%20P_A%29%3DE_%7BP_B%7D%5Cleft%5B%20%5Clog_2%281%2FP_A%28%5Comega%29%29%20-%20%5Clog_2%281%2FP_B%28%5Comega%29%29%20%5Cright%5D%3D0.5%20%282-1%29%2B0.25%20%282-2%29%2B0.125%20%282-3%29%2B0.125%20%282-3%29%3D0.25%20%5Cend%7Bcases%7D)
ここではたまたま になっていますが、一般に、KL情報量は確率分布の交換について非対称です。「A国の天気をB国方式でエンコードしたときのビット長の無駄」と「A国の天気をB国方式でエンコードしたときのビット長の無駄」は一般には等しくなりません。例えば、天気が晴れにしかならないC国では、晴れ以外の天気は無限大のコード長をもつことになるので、C国の方式で他の国の天気をエンコードした交差エントロピーも、カルバック・ライブラー情報量も無限大になります。しかし、他の国の方式でC国の天気をエンコードした場合は無限大にはなりません。
になっていますが、一般に、KL情報量は確率分布の交換について非対称です。「A国の天気をB国方式でエンコードしたときのビット長の無駄」と「A国の天気をB国方式でエンコードしたときのビット長の無駄」は一般には等しくなりません。例えば、天気が晴れにしかならないC国では、晴れ以外の天気は無限大のコード長をもつことになるので、C国の方式で他の国の天気をエンコードした交差エントロピーも、カルバック・ライブラー情報量も無限大になります。しかし、他の国の方式でC国の天気をエンコードした場合は無限大にはなりません。
![\begin{cases} H(P_A, P_C)=E_{P_A}\left[ \log_2(1/P_C(\omega)) \right]=+\infty \\ H(P_C, P_A)=E_{P_C}\left[ \log_2(1/P_A(\omega)) \right]=2 \end{cases}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cbegin%7Bcases%7D%20H%28P_A%2C%20P_C%29%3DE_%7BP_A%7D%5Cleft%5B%20%5Clog_2%281%2FP_C%28%5Comega%29%29%20%5Cright%5D%3D%2B%5Cinfty%20%5C%5C%20H%28P_C%2C%20P_A%29%3DE_%7BP_C%7D%5Cleft%5B%20%5Clog_2%281%2FP_A%28%5Comega%29%29%20%5Cright%5D%3D2%20%5Cend%7Bcases%7D)

![\begin{cases} H(P_B, P_C)=E_{P_B}\left[ \log_2(1/P_C(\omega)) \right]=+\infty \\ H(P_C, P_B)=E_{P_C}\left[ \log_2(1/P_B(\omega)) \right]=1 \end{cases}](http://chart.apis.google.com/chart?cht=tx&chl=%20%5Cbegin%7Bcases%7D%20H%28P_B%2C%20P_C%29%3DE_%7BP_B%7D%5Cleft%5B%20%5Clog_2%281%2FP_C%28%5Comega%29%29%20%5Cright%5D%3D%2B%5Cinfty%20%5C%5C%20H%28P_C%2C%20P_B%29%3DE_%7BP_C%7D%5Cleft%5B%20%5Clog_2%281%2FP_B%28%5Comega%29%29%20%5Cright%5D%3D1%20%5Cend%7Bcases%7D)

KL情報量は2つの分布の間の距離のようなものと表現されることがあります。KL情報量は非対称なので、 は
は  から見た
から見た  の近さといった方がいいのかもしれません。
の近さといった方がいいのかもしれません。
ところで、機械学習では、分類器を学習するときに、正解の分布 と分類器の予測分布
と分類器の予測分布  の交差エントロピー
の交差エントロピー  を損失関数とすることがよくあります。交差エントロピーは
を損失関数とすることがよくあります。交差エントロピーは  のときに最小となるので、分類器を学習して
のときに最小となるので、分類器を学習して  を
を  に近づくよう改善していく作業は、正解の分布に合わせてエンコードを最適化しようとする作業に似ています。
に近づくよう改善していく作業は、正解の分布に合わせてエンコードを最適化しようとする作業に似ています。 が固定ならば、
が固定ならば、 の最小化は
の最小化は  の最小化に他なりません。また、学習の初期にC国のような分布からはじめてしまうと、正解の分布から見た距離がどうしようもなく遠くなってしまうことが予想されます(ちょうどA国の分布から見たC国の分布の交差エントロピーが無限大であるように)。
の最小化に他なりません。また、学習の初期にC国のような分布からはじめてしまうと、正解の分布から見た距離がどうしようもなく遠くなってしまうことが予想されます(ちょうどA国の分布から見たC国の分布の交差エントロピーが無限大であるように)。
分布と分布がどれだけずれているかの尺度は何も交差エントロピーだけでなく、2乗誤差なども考えられます。2乗誤差も交差エントロピーも、小さくなるようにパラメータを更新し続ければ分類器が改善していくことが期待されます。交差エントロピーの利点は、分布がまるで期待外れのとき(誤差が大きいとき)学習の速度が速い点です。2乗誤差は、誤差が大きいときに必ずしも学習が速くなりません。例えばシグモイド関数やソフトマックス関数で活性化された分類器の出力があるクラスにかなり偏ってしまっているとき、それが期待とはほど遠い状態であるにもかかわらず、2乗誤差の勾配はとてもなだらかになってしまいます。この状態でパラメータを少し動かしたところで、分布はほとんど変わらず、2乗誤差はほぼ変わらないからです。交差エントロピーの場合、分類器の出力が期待せずかなり偏ってしまった場合、真の分布から見た交差エントロピーがそれこそ無限大の勢いで大きくなるので(A国の分布から見たC国の分布の交差エントロピーのように)、勾配も大きくなります。この期待外れの時に勾配が大きいという望ましい性質により、交差エントロピーは広く採用されています。
でも冷静に考えると交差エントロピーが何かよくわかりませんでした。むしろエントロピーがわかりませんでした。
以下の記事を読み、もっと無理がない例で短くまとめたかったのですが、やはり例に無理があり、長くなってしまいました。
参考文献
- 情報理論を視覚的に理解する (1/4) | コンピュータサイエンス | POSTD
- 情報理論を視覚的に理解する (2/4) | コンピュータサイエンス | POSTD
- 情報理論を視覚的に理解する (3/4) | コンピュータサイエンス | POSTD
- 情報理論を視覚的に理解する (4/4) | コンピュータサイエンス | POSTD
- ニューラルネットワークと深層学習
以下はこれら記事の劣化アレンジです。
A国、B国、C国があります。
A国では、一日の天気は25%ずつの確率で晴れ、曇り、雨、雪になります。B国では、晴れになる確率が50%、曇りになる確率が25%、雨か雪になる確率が12.5%ずつです。C国では天気は晴れにしかなりません。この3国の天気の確率関数をグラフに表すと以下のようになります。

または、それぞれの天気になる確率を横向きの積み上げ棒グラフで表すと以下のようになります。

あるとき、A国の気象庁に勤めるアリスは、A国内の大学から「過去の天気のデータをなるべくたくさんの日数ほしい」と申請を受けました。A国の法律で、気象庁からの情報提供は1枚のフロッピーディスク(死語)によって行うことになっていましたが、この架空の世界では記録媒体技術が残念だったのでフロッピーディスクの容量が1KB(8000ビット)しかありませんでした。しかも経費削減のため1件の情報提供にディスクは1枚しかつかえませんでした。そこで、アリスは容量を最大限に活用するためそれぞれの天気を「晴:00、曇:01、雨:10、雪:11」にエンコードし、1日の天気の情報を2ビットで表現することで、4000日分のデータを提供しました(8000 ÷ 2 = 4000)。
同じころ、B国の気象庁に勤めるボブもB国内の大学から同じ申請を受けました。B国も情報提供に係る制約はA国と同じです。ボブは、最初はアリスのように「晴:00、曇:01、雨:10、雪:11」というエンコードで情報を提供しようとしましたが、B国ではそれぞれの天気の確率に偏りがあることに気付きました。ボブは「晴:0、曇:10、雨:110、雪:111」と、確率が大きい晴れに短いビット数を割り振り、その代わり確率が小さい雨と雪に長いビット数を割り振ることで、1日の天気の情報の平均ビット数を 0.5*1 + 0.25*2 + 0.125*3 + 0.125*3 = 1.75 ビットにしました。こうすることで、8000ビットのディスクで4500日以上分のデータを提供しました(8000 ÷ 1.75 > 4500)。

アリスよりボブが同じ容量のディスクでよりたくさんの日数の情報を提供できたのは、ボブの方が優れたエンコードをしたからではありません。何ならクリスはディスクをつかうまでもなく無限の日数の情報を提供できています。1回の試行の結果(ある1日の天気)を伝えるのに必要な平均ビット数の最小値は確率分布によってのみ決まります。つまり、確率
A国、B国、C国それぞれの、「1日の天気を調べる」という試行のエントロピーは以下です。
情報量を「その試行の結果を知らされたときの価値」、エントロピーを「1回の試行の結果の結果を知らされたときの価値の期待値」と解釈する人もあります。あるできごとを知らされたときの価値は、そのできごとが珍しいほど高くなります。A国ではどの天気になる確率も等しいので、どの天気だと知らされても等しく2の価値があります。B国では晴れになる確率が高いので、晴れだと知らされたときの価値は1しかありませんが、雨や雪になる確率は低いので、雨や雪だと知らされたときの価値は3あります。また、C国で晴れだと知らされても価値は0です。この価値の平均としてのエントロピーは不確実さが大きいほど(確率分布がばらつくほど)大きくなります。天気の不確実さは A国 > B国 > C国 の順になっているといえるでしょう。
ところであるとき、B国の大学でA国の天気のデータが必要になりました。B国の大学の人はボブ式のエンコードに慣れていたので、A国のアリスに、B国のボブ式のエンコードでA国の天気のデータを送るよう依頼しました。アリスは言われた通りにしましたが、A国の天気をボブ式にエンコードすると、1日あたりの平均ビット長が 1*0.25 + 2*0.25 + 3*0.25 + 3*0.25 = 2.25 になってしまうことに気付きました。この世界の残念なフロッピーディスクでは3600日分のデータも提供することができませんでした(8000 ÷ 2.25 < 3600)。
同じころボブもA国の大学の人にアリス式のエンコードでB国の天気データを提供するよう要請されました。アリス式のエンコードはどの天気にも2ビットをあてがうので、B国の天気をエンコードしても平均ビット長が2ビットになりました。ボブは、「自分のエンコードなら、この国の天気を1日あたり1.75ビットに圧縮できるのになあ」と思いました。

ある確率分布に最適化された方式で別の確率分布をエンコードしたときの平均ビット長を交差エントロピーとよびます。
これはエンコードを誤ったようなイメージです。エンコードを誤ると、めずらしいできごとに小さなビット長を割り振ってしまう影響よりも、めずらしくないできごとに大きなビット長を割り振ってしまう影響の方が必ず大きくなり、必要な平均ビット長が大きくなってしまいます(
このビット長の無駄/価値の誤差
ここではたまたま
KL情報量は2つの分布の間の距離のようなものと表現されることがあります。KL情報量は非対称なので、
ところで、機械学習では、分類器を学習するときに、正解の分布
分布と分布がどれだけずれているかの尺度は何も交差エントロピーだけでなく、2乗誤差なども考えられます。2乗誤差も交差エントロピーも、小さくなるようにパラメータを更新し続ければ分類器が改善していくことが期待されます。交差エントロピーの利点は、分布がまるで期待外れのとき(誤差が大きいとき)学習の速度が速い点です。2乗誤差は、誤差が大きいときに必ずしも学習が速くなりません。例えばシグモイド関数やソフトマックス関数で活性化された分類器の出力があるクラスにかなり偏ってしまっているとき、それが期待とはほど遠い状態であるにもかかわらず、2乗誤差の勾配はとてもなだらかになってしまいます。この状態でパラメータを少し動かしたところで、分布はほとんど変わらず、2乗誤差はほぼ変わらないからです。交差エントロピーの場合、分類器の出力が期待せずかなり偏ってしまった場合、真の分布から見た交差エントロピーがそれこそ無限大の勢いで大きくなるので(A国の分布から見たC国の分布の交差エントロピーのように)、勾配も大きくなります。この期待外れの時に勾配が大きいという望ましい性質により、交差エントロピーは広く採用されています。