強化学習：ノート12 - クッキーの日記

読んでいる本（出典）：強化学習 : Richard S.Sutton, Andrew G.Barto, 三上貞芳, 皆川雅章 : 本 : Amazon.co.jp

前回：ノート11 ／次回：まだ
目次：強化学習

読んだページ： 147～156ページ
以下、自分の理解。

これまでのあらすじ：強化学習の解法であるTD学習は、方策を評価するためにその方策をつかったエピソードをどんどん生成していく点ではモンテカルロ法っぽいけど、価値関数を更新するのに1エピソードの終了まで待たず、次ステップの状態の価値の現在の推定値を用いてステップごとに価値関数を更新していく（ブートストラップする）点が異なる。
- ブートストラップすると、1エピソードが終わる前に価値の推定を更新できる。基本的にブートストラップする方が賢いし直感的なはず。145～147ページの車通勤問題で、渋滞にはまったら帰宅してみるまでもなく自宅までの所要時間の見積もりを更新できる、というのがわかりやすい例。例えば将棋をやっていても負けるまでもなくこれはもう形勢不利だということはあるはず。ただブートストラップによる価値推定が完全に優位ということではなく、ブートストラップしないモンテカルロ法では「マルコフ性を乱して悪い影響が出る度合いが少ない（140ページ）」とある。
  - いまいち上の下線部がわかっていない。確かに推定値からの推定をしない方が、変に価値を見誤る危険は低そうにみえる。でもブートストラップでも見誤りはしないはずで。ブートストラップは Bellman 方程式の平衡にのっかっているから、マルコフ性が厳密には成り立たない影響は受けやすいのかもしれない。

TD(0) がモンテカルロ法より強い※理由（154ページ）：モンテカルロ法はサンプルデータ上での誤差を小さくするのにとどまるのに対し、TD(0) はマルコフ過程モデルを最尤推定にいっているから。 ※ いつも強いとは限らない。
- TD(0) の更新式は Bellman 方程式の平衡にのっかっているからそうなんだろうというレベルの理解。
- 確実性等価推定って言葉が確実性等価額っぽい。意味合いは全然違う。
  - 確実な50万と多分100万あなたはどっち？期待効用仮説｜ミクロ経済学(15) | 重要論点がわかる！中小企業診断士ブログ

TD による方策評価で実際に強化学習問題を解くとき、モンテカルロ法同様、方策オン型と方策オフ型がある（155ページ）。前者の例が Sarsa で、後者の例がQ学習。
- Sarsa の読み方わかりません。わからなくてもいいんだけど、人と話すとき「読み方サーサでいいかわかんないけどサーサ」になって長いのでつらい。

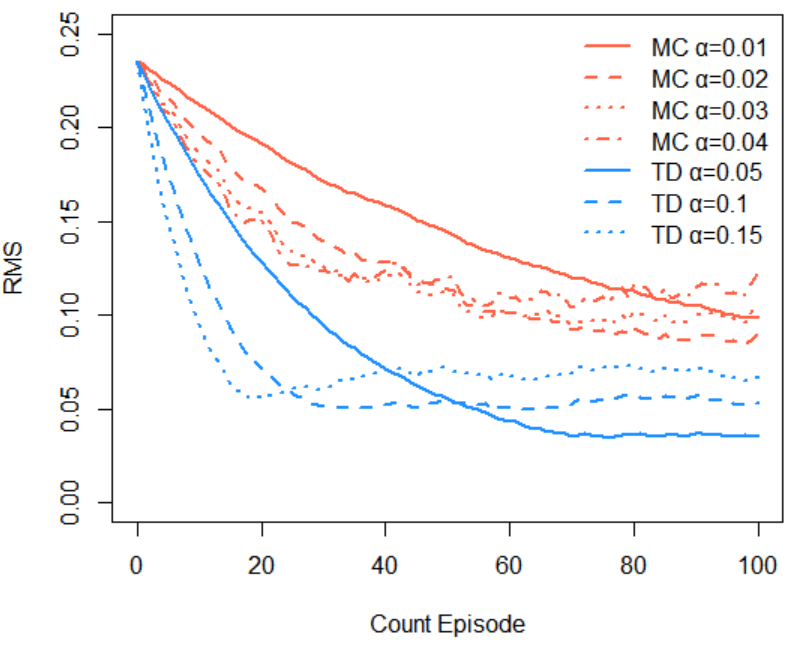
149～151ページの、ランダムウォークに対する価値推定の例。
下図左側は151ページの図 6.7 と同じになっている。右側はモンテカルロ法を逐一訪問ではなく初回訪問にした例。

「このタスクでは、エピソード数にかかわらず、TD法がMC法より常に良い性能を示していることがわかる（149ページ）」とあるけど、初回訪問にすると $\alpha$ によってはMC法もよく見えるんですが。
じゃあ逐一訪問と初回訪問の違いは「非常に類似しているが、理論的な性質はわずかに異なっている（120ページ）」としかないのでよくわからないんだけど、同ページに第7章で逐一訪問MCを再考すると書いてあるからそのとき考えよう。

f:id:cookie-box:20160416160036p:plain:w360

f:id:cookie-box:20160416160045p:plain:w360

# 1エピソードの取得
GetEpisode <- function() {
  s <- c(3)
  current <- 3
  while(TRUE) {
    rand <- ifelse(floor(2.0 * runif(1))==0, -1, 1)
    current <- current + rand
    if (current == 6) {
      return(list(s=s, reward=1))
    }
    if (current == 0) {
      return(list(s=s, reward=0))
    }
    s <- c(s, current)
  }
}

# MC による価値の更新
UpdateMC <- function(alpha, v, episode, reward) {
  # episode <- unique(episode) # このコメントアウトを外すと初回発生に対してのみ価値を更新する
  n <- length(episode)
  for (i in 1:n) {
    v[[ episode[[i]] ]] <- v[[ episode[[i]] ]] + alpha * (reward - v[[ episode[[i]] ]])
  }
  return(v)
}

# TD による価値の更新
UpdateTD <- function(alpha, v, episode, reward) {
  n <- length(episode)
  for (i in 1:(n-1)) {
    v[[ episode[[i]] ]] <- v[[ episode[[i]] ]] + alpha * (v[[ episode[[i+1]] ]] - v[[ episode[[i]] ]])
  }
  v[[ episode[[n]] ]] <- v[[ episode[[n]] ]] + alpha * (reward - v[[ episode[[n]] ]])
  return(v)
}

# 真の価値
v.answer <- c(1.0/6.0, 2.0/6.0, 3.0/6.0, 4.0/6.0, 5.0/6.0)
# 真の価値からの2乗平均平方根誤差
GetRMS <- function(v) {
  return(sqrt(mean((v - v.answer) * (v - v.answer))))
}

# ------------------------------ START MAIN ------------------------------
alpha.MC <- c(0.01, 0.02, 0.03, 0.04)
alpha.TD <- c(0.05, 0.1, 0.15)
RMS.MC.all <- list(NULL, NULL, NULL, NULL)
RMS.TD.all <- list(NULL, NULL, NULL)
# テキストにならって以下を100回試行
for (trial in 1:100) {
  # 価値関数の推定に用いる100個のエピソードを生成
  episodes <- list()
  rewards <- c()
  for (i in 1:100) {
    episode <- GetEpisode()
    episodes <- c(episodes, list(episode$s))
    rewards <- c(rewards, episode$reward)
  }
  # モンテカルロ法、TD用の価値関数を初期化
  v.init <- c(0.5, 0.5, 0.5, 0.5, 0.5)
  v.MC <- list(v.init, v.init, v.init, v.init)
  v.TD <- list(v.init, v.init, v.init)
  RMS.MC <- list(c(GetRMS(v.MC[[1]])), c(GetRMS(v.MC[[2]])), c(GetRMS(v.MC[[3]])), c(GetRMS(v.MC[[4]])))
  RMS.TD <- list(c(GetRMS(v.TD[[1]])), c(GetRMS(v.TD[[2]])), c(GetRMS(v.TD[[3]])))
  # 逐次推定
  for (i in 1:100) {
    for (i.alpha in 1:length(alpha.MC)) {
      v.MC[[i.alpha]] <- UpdateMC(alpha.MC[[i.alpha]], v.MC[[i.alpha]], episodes[[i]], rewards[[i]])
      RMS.MC[[i.alpha]][[i+1]] <- GetRMS(v.MC[[i.alpha]])
    }
    for (i.alpha in 1:length(alpha.TD)) {
      v.TD[[i.alpha]] <- UpdateTD(alpha.TD[[i.alpha]], v.TD[[i.alpha]], episodes[[i]], rewards[[i]])
      RMS.TD[[i.alpha]][[i+1]] <- GetRMS(v.TD[[i.alpha]])
    }
  }
  for (i.alpha in 1:length(alpha.MC)) {
    RMS.MC.all[[i.alpha]] <- cbind(RMS.MC.all[[i.alpha]], RMS.MC[[i.alpha]])
  }
  for (i.alpha in 1:length(alpha.TD)) {
    RMS.TD.all[[i.alpha]] <- cbind(RMS.TD.all[[i.alpha]], RMS.TD[[i.alpha]])
  }
}

# プロット
RMS.MC.mean <- list(NULL, NULL, NULL, NULL)
RMS.TD.mean <- list(NULL, NULL, NULL)
for (i.alpha in 1:length(alpha.MC)) {
  RMS.MC.mean[[i.alpha]] <- apply(RMS.MC.all[[i.alpha]], MARGIN=1, FUN=mean)
}
for (i.alpha in 1:length(alpha.TD)) {
  RMS.TD.mean[[i.alpha]] <- apply(RMS.TD.all[[i.alpha]], MARGIN=1, FUN=mean)
}
plot(c(0, 100), c(0, 0.25), xlab="Count Episode", ylab="RMS", type="n")
lines(0:100, RMS.MC.mean[[1]], col="tomato", lwd=2)
lines(0:100, RMS.MC.mean[[2]], col="tomato", lwd=2, lty=2)
lines(0:100, RMS.MC.mean[[3]], col="tomato", lwd=2, lty=3)
lines(0:100, RMS.MC.mean[[4]], col="tomato", lwd=2, lty=4)
lines(0:100, RMS.TD.mean[[1]], col="dodgerblue", lwd=2)
lines(0:100, RMS.TD.mean[[2]], col="dodgerblue", lwd=2, lty=2)
lines(0:100, RMS.TD.mean[[3]], col="dodgerblue", lwd=2, lty=3)
legend("topright", legend=c("MC α=0.01", "MC α=0.02", "MC α=0.03", "MC α=0.04", "TD α=0.05", "TD α=0.1", "TD α=0.15"),
  col=c(rep("tomato", 4), rep("dodgerblue", 3)), lty=c(1, 2, 3, 4, 1, 2, 3), lwd=2, box.lwd=NA)

練習問題 6.1

TD更新がモンテカルロ更新よりもよい平均性能を示す場合について。
この問題の意図がつかみきれていないけど、145ページの例で、実は最初から帰宅時刻の見積もり（＝状態価値関数）はほぼ適切で、「車に乗る．雨」「一般道．トラックの後ろ」に関してだけ見積もりが長すぎ、短すぎであったとする。そう考えてもたぶん不自然ではない。でも、モンテカルロ法だとどの状態の価値も（きっとトラックの後ろについたことのせいで）「所要時間はもっと長め」に更新されてしまう（「車に乗る．雨」に対しては、正解からかえって遠ざかってしまうことになる）。モンテカルロ法を進めるうちにそれは是正されていくはずだが、効率的ではないはず。一方TD学習では「車に乗る．雨」はちゃんと短めに更新されている。

練習問題 6.2
最初のエピソードが左端の終端状態で終わったことを意味している。
正確な変更量は -0.05 = 0.1 * (0 - 0.5)

練習問題 6.3
はるかに良い結果は得られないのでは。 $\alpha$ を小さくすれば学習が遅くなり、大きくすれば直近の値を重んじてしまって不安定になるのだから。むしろ最適な学習係数を教えてほしいんですが。
f:id:cookie-box:20160416164724p:plain:w320

練習問題 6.4
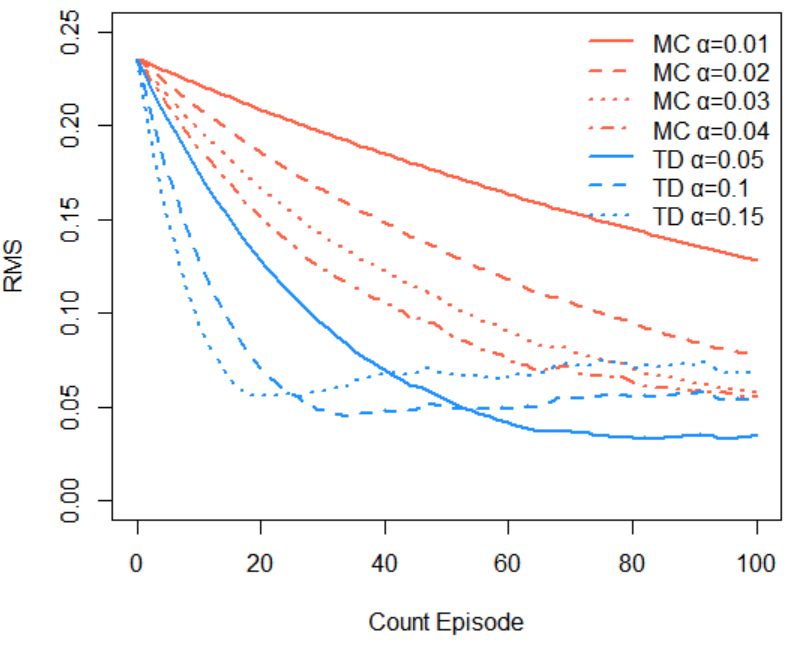
初期値によっては小さくなって → 大きくなる現象は起こらない（下図）。
150ページの図 6.6 がどんな形からはじまり、どんな風に変化して「真の価値」に向かうかという話だと思うが、この初期値0.5が通過するRMS誤差が小さい点が、価値関数として真のものに近い（近いって何）ということでもないのだろうか。よくわかりません。
f:id:cookie-box:20160416170056p:plain:w320

練習問題 6.5
各状態から左端に抜ける確率を $p_\ast$ とすると以下が成り立つので連立して解く。
$p_A = \frac{1}{2}p_B \; , \; p_B = \frac{1}{2}p_A + \frac{1}{2}p_C \; , \; p_C = \frac{1}{2}p_B + \frac{1}{2}p_D \; , \; p_D = \frac{1}{2}p_C + \frac{1}{2}p_E \; , \; p_E = \frac{1}{2}p_D + \frac{1}{2}$

TD学習も実装したいけど、簡単で面白い例がないかな。