Rによるベイジアン動的線型モデル：ノート4

読んでいる本（出典）： Rによるベイジアン動的線形モデル (統計ライブラリー) | G.ペトリス, S.ペトローネ, P.カンパニョーリ, 和合肇, 萩原淳一郎 | 本 | Amazon.co.jp

今日読んだページ： 22～35ページ
以下、自分の解釈。誤っている可能性があります。

前回までのあらすじ：
- 線形回帰モデルに対しても共役な事前分布を選択し、回帰係数／分散共分散行列／その両方のベイズ推定が可能。
マルコフ連鎖モンテカルロ法の導入：
- しばしばパラメータ $\psi$ の事後分布は陽に扱えない。→ そこでモンテカルロ法。
- 事後分布からの標本はマルコフ連鎖によりシミュレーションするのが標準的。
- 一般的なマルコフ連鎖モンテカルロ法：
  - ギブス・サンプラー（弱点：条件付分布からの標本化が難しいとき、目標分布が多峰的なとき）
  - メトロポリス - ヘイスティングス・アルゴリズム（弱点：一般的にサンプルに従属性がある）
- 適応棄却メトロポリス・サンプリング（ARMS）：
  - 棄却サンプリング：目標分布に似た提案分布を使用し、受容確率により採否を判定。
  - 適応棄却サンプリング：棄却が発生したときに提案分布を目標分布に近づけるよう更新。
    下図のようなイメージ。但し、（Cに）無駄があるような絵。

R ではパッケージ dlm に ARMS が含まれているということなのでつかってみる。
元旦にちなんだ確率分布をつくる。→ 2000点サンプリング → できた（ARMSの無駄遣いが）。
f:id:cookie-box:20160101183451p:plain:w450

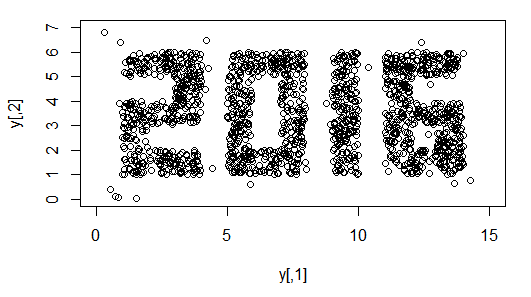
コード（どうでもいい）は以下。ARMS が対数密度を使用する都合上、"2016" の文字の外も0でない密度がある（on と off の密度差を contrast で定義 = 100.0）。

my.dens <- function(x) {
  contrast <- 100.0
  off <- 1.0
  on <- contrast
  z <- on * 40 + off * 65
  off <- off / z
  on <- on / z
  if (x[[1]] < 1 || 15 <= x[[1]] || x[[2]] < 1 || 6 <= x[[2]]) {
    return(off)
  }
  if (5 <= x[[1]] && x[[1]] < 6) { return(on) }
  if (7 <= x[[1]] && x[[1]] < 8) { return(on) }
  if (9 <= x[[1]] && x[[1]] < 10) { return(on) }
  if (11 <= x[[1]] && x[[1]] < 12) { return(on) }
  if (x[[2]] < 2 || 5 <= x[[2]]) {
    if (1 <= x[[1]] && x[[1]] < 4) { return(on) }
    if (6 <= x[[1]] && x[[1]] < 7) { return(on) }
    if (12 <= x[[1]] && x[[1]] < 14) { return(on) }
  } else if (x[[2]] < 3) {
    if (1 <= x[[1]] && x[[1]] < 2) { return(on) }
    if (13 <= x[[1]] && x[[1]] < 14) { return(on) }
  } else if (x[[2]] < 4) {
    if (1 <= x[[1]] && x[[1]] < 4) { return(on) }
    if (12 <= x[[1]] && x[[1]] < 14) { return(on) }
  } else {
    if (3 <= x[[1]] && x[[1]] < 4) { return(on) }
  }
  return(off)
}
my.log.dens <- function(x) { return(log(my.dens(x))) }
supp <- function(x) { (0 <= x[[1]] && x[[1]] < 15 && 0 <= x[[2]] && x[[2]] < 7) }
y <- arms(c(1, 1), my.log.dens, supp, 2000)
plot(y, xlim=c(0, 15), ylim=c(0, 7))

演習問題をやりたかったができていない。